
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В процессе исключений метода гаусса не может возникнуть более m не нулевых ведущих элементов или не нулевых ведущих строк то число свободных переменных не может быть меньше чем n-m.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Каждая однородная система АХ=0 имеющая больше неизвестных чем уравнений имеет хотя б одно не нулевое решение
7. Понятие линейной зависимости арифметических векторов (примеры) Система векторов e 1, e 2,..., e k линейного пространства L называется линейно независимой системой, если равенство С1· e 1+С2 ·e 2+...+Сk · e k = 0 возможно только когда все коэффициенты С1, С2,..., Сk равны нулю. Здесь 0 — нулевой вектор линейного пространства L, С1, С2,..., Сk — числовые коэффициенты. Если система векторов e 1, e 2,..., e k линейного пространства L не является линейно независимой системой, то она называется линейно зависимой системой векторов. пример Система векторов · i, j линейного пространства R2 геометрических радиусов векторов плоскости линейно независима. Действительно. i = (1, 0), j = (0, 1), С 1 · i + С 2 · j = (С 1, С 2), а из (С 1, С 2) = 0 следует, что С 1 = 0 и С 1 = 0, т.е. система векторов i, j из R2 линейно независима.
8. Понятие базиса системы арифметических векторов (примеры) Второе определение базиса систем векторов базисная система векторов v1 v2…. vk с n компонентами. Базисом этой системы векторов называется такое подмножество w1 w2 ….wr линейно-независимых, что любой v1 v2 …vk выражается в виде линейной комбинации векторов w1 w2 ….wr. Ба́зис (др.-греч. βασιζ, основа) — множество таких векторов в векторном пространстве, что любой другой вектор пространства может быть единственным образом представлен в виде линейной комбинации базисных векторов.
9. Понятие ранга матрицы. Теорема о ранге ступенчатой матрицы. Рангом системы векторов v1 v2…. vk называется число базисных векторов данной системы. Ранг системы столбцов матрицы равен рангу системы строк матрицы Если матрица A не нулевая, т.е. существует хотя бы один aij элемент матрицы A, отличный от нуля, тогда всегда можно указать натуральное число r такое, что у матрицы A имеется минор r- го порядка, для которого Δr всякий минор матрицы A порядка r+1 и выше равен нулю, тогда число r, обладающее указанными свойствами называется рангом матрицы A и обозначается r = RgA. ранг любой прямоугольной матрицы не должен быть больше, чем минимальный размер матрицы. Если матрица квадратная, то ранг не может быть больше, чем размер матрицы. Математически это можно выразить так r
если все элементы матрицы A равны нулю, т. е. aij=0, то ранг этой матрицы тоже будет равен нулю r = RgA = 0. Ранг ступенчатой матрицы А равен числу её не нулевых строк или столбцов содержащих ведущие элементы.
10. Теорема о равенстве ранге произвольной матрицы А и эквивалентной ей ступенчатой матрицы (поясните на примере)
11. Теорема о существование ненулевого решения однородной системы линейных алгебраических уравнений с прямоугольной матрицей. Фундаментальная система решений. Однородные системы Однородной системой линейных уравнений называется система вида: Нулевое решение
В матричной форме АХ=0 Однородная система всегда совместна тк существует тривиальное решение х1=х2=хn=0 Система не определена когда ранг матрицы меньше числа неизвестных Теорема (о структуре общего решения). § если § если
Теорема (о ФСР). § ФСР (1) существует: § она состоит из § общее решение системы имеет вид Замечание:
Пример Решим систему Перепишем её в матричном виде:
Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:
Таким образом ранг системы (ранг её основной матрицы) равен двум. Это значит, что существует Перепишем полученную систему в виде уравнений:
Возьмём
Подставим по очереди единицы в качестве одной из свободных переменных:
Тогда общее решение рассматриваемой системы может быть записано так:
а вектора
12. Структура решения неоднородной системы линейных алгебраических уравнений.
Неоднородной системой линейных уравнений называется система вида:
§ если § если Пример Решим систему Преобразуем её к Тогда переменные Заметим, что Составим однородную систему: Тогда, подставив единицу в качестве свободной переменной
Общее решение системы может быть записано так:
13. Теорема о связи ранга квадратной матрицы и ее определителя. Решение однородной и неоднородной систем уравнений с квадратной матрицей. Пусть
14. Понятие геометрического вектора. Линейные операции над векторами.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.190.247 (0.011 с.) |

 0;
0; min(m,n).
min(m,n).


 системы (1) называется тривиальным решением.
системы (1) называется тривиальным решением.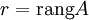 , тогда:
, тогда: , где
, где  — число переменных системы, то существует только тривиальное решение;
— число переменных системы, то существует только тривиальное решение; , то существует
, то существует  линейно независимых решений рассматриваемой системы:
линейно независимых решений рассматриваемой системы:  , причём её общее решение имеет вид:
, причём её общее решение имеет вид:  , где
, где  — некоторые константы.
— некоторые константы.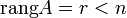 , где
, где  ;
; векторов;
векторов; .
. , то ФСР не существует.
, то ФСР не существует.


 линейно независимых решения системы.
линейно независимых решения системы.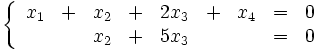
 и
и  в качестве главных переменных. Тогда:
в качестве главных переменных. Тогда:
 и
и  .
.
 ,
, составляют фундаментальную систему решений.
составляют фундаментальную систему решений.
 — её расширенная матрица.
— её расширенная матрица. (т.е. система (2) совместна), тогда:
(т.е. система (2) совместна), тогда: , где
, где  — общее решение системы (1), называемое общим однородным решением,
— общее решение системы (1), называемое общим однородным решением,  — частное решение системы (2), называемое частным неоднородным решением.
— частное решение системы (2), называемое частным неоднородным решением.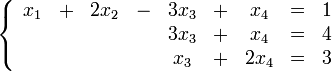

 и
и  обязательно будут главными, возьмём также
обязательно будут главными, возьмём также  является частным решением.
является частным решением.


 . Определитель матрицы
. Определитель матрицы  равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен
равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен 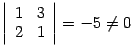 . Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.
. Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.


