Иллюстрация: модель с двумя объясняющими переменными

Множественный регрессионный анализ является развитием парного регрес­сионного анализа применительно к случаям, когда зависимая переменная ги­потетически связана с более чем одной объясняющей переменной. Большая часть анализа будет непосредственным расширением парной регрессионной модели, но здесь мы сталкиваемся с двумя новыми проблемами. Во-первых, при оценке влияния данной объясняющей переменной на зависимую пере­менную нам придется решать проблему разграничения ее воздействия и воз­действий других объясняющих переменных. Во-вторых, мы должны будем ре­шить проблему спецификации модели. Часто предполагается, что несколько переменных могут оказывать влияние на зависимую переменную, с другой стороны, некоторые переменные могут не подходить для модели. Мы должны решить, какие из них следует включить в уравнение регрессии, а какие — ис­ключить из него. Вторая проблема будет рассмотрена в гл. 6. В данной главе мы полагаем, что спецификация модели правильная. В большинстве ситуаций мы ограничимся базовым случаем, где используются только две объясняющие пе­ременные.

Начнем с рассмотрения примера с факторами, определяющими величину заработка. Расширим первоначальную модель, включив учет влияния числа лет работы наряду с образованием, и допустим, что истинную зависимость можно выразить следующим образом:

EARNINGS = β₁ + β₂5 + β₃ EXP + w, (3.1)

 

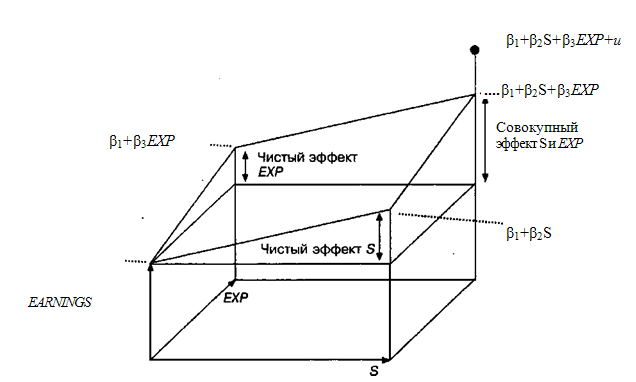
где EARNINGS— часовой заработок; S— продолжительность обучения (число полных лет учебы); ЕХР — число лета работы после получения образования; и — случайный член. Такая модель, разумеется, является значительным упрощением как с точки зрения состава независимых переменных, включен­ных в зависимость, так и с точки зрения математической формулы связи.

Для геометрической иллюстрации этой зависимости необходима трехмерная диаграмма с отдельными осями для EARNINGS, S и ЕХР, как показано на рис. 3.1. Основание на рисунке содержит оси для S и ЕХР, и если пренебрег текущим влиянием случайного члена, то наклонная плоскость над ним показывает величину EARNINGS, соответствующую любому сочетанию (S, EXP), измеренную расстоянием по вертикали до этой плоскости над основанием в данной точке. Так как заработки могут увеличиваться под влиянием как продолжительности обучения, так и опыта работы, изображение на диаграмм было построено на основе допущения о том, что β₂ и β₃ положительны. Буквально свободный член β₁ показывает ожидаемую величину заработка при первом сроке обучения и нулевом опыте работы. Однако такая интерпретаций была бы некорректной, поскольку в выборке NLSY не было лиц с нулевым сроком обучения. В действительности лишь очень немногие в этой выборке не завершили 8-летнее образование. Математическая формула (3.1) означает, что если бы ЕХР равнялось нулю, то для любого положительного S заработок раз­нялся бы β₁ + β₂S, где приращение β₂S показывает «чистый эффект S» в будущем. При S, равном нулю, уравнение показывает, что при любой положительной величине ЕХР заработок был бы равен β₁ + β₂S, где приращение β₂S показывает «чистый эффект ЕХР». На рис. 3.1 показан также совокупный эффект продолжительности обучения и опыта работы β₂S + β₃ ЕХР.

До сих пор мы пренебрегали случайным членом. Если он отсутствует в ураз нении (3.1), то значения переменной EARNINGS в данной выборке наблюдений для EARNINGS, S и ЕХР будут находиться точно на обозначенной наклонной плоскости, и будет довольно просто вывести точные значения для β ₁, β ₂ и β₃ (это не так просто сделать геометрически, если вы не имеете достаточно большого опыта в создании трехмерных моделей, однако это довольно просто сделать алгебраическим путем).

 

 

Рисунок 3.1 – Истинная модель с двумя объясняющими переменными: заработок как функция продолжительности обучения и опыта работы

Наличие случайного члена приводит к тому, что фактические значения ве­личины заработка будут лежать несколько выше или несколько ниже значе­ний, соответствующих данной наклонной плоскости. Следовательно, теперь мы имеем трехмерный аналог для двумерной задачи, показанной на рис. 1.2. Вместо нахождения линии, соответствующей двумерному рассеянию точек, мы теперь должны расположить плоскость так, чтобы она соответствовала трехмерному рассеянию. Уравнение для выбранной плоскости будет иметь вид

EARNINGS = b₁ + b₂S + b₃EXP, (3.2)

и ее расположение будет зависеть от выбора величин b₁ b₂, и b₃ являющихся соответственно оценками β₁, β₂ и β₃. При использовании набора данных EAEF 21 мы получим распечатку результатов оценивания регрессии, представ­ленную в табл. 3.1.

Оцененное уравнение интерпретируется следующим образом. На каждый дополнительный полный год обучения при данном опыте работы приходится увеличение часового заработка в размере 2,68 долл. На каждый дополнитель­ный год опыта работы при данной продолжительности обучения приходится увеличение часового заработка в размере 0,56 долл. Постоянный член не имеет здесь содержательной интерпретации. Буквально он означал бы, что респон­дент с нулевым уровнем образования (на самом деле все респонденты учились не менее шести лет) и без опыта работы зарабатывал бы в час минус 26,49 долл.

Таблица 3.1

 

EARNINGS S EXP
Source	SS	df	MS		Number of obs =F(2,537) =
Model	22513.6473		11256.8237		F(2,537)	67.54
Residual	89496.5838		166.660305		Prob > F = R-squared Adj R-squared Root MSE	0.0000 0.2010 0.1980 12.91
Total	112010.231		207.811189
EARNINGS	Coef.	Std. Err.	t	P>|t|	[95% Conf.	Interval]
S	2.678125	.2336497	11.46	0.000	2.219146	3.137105
EXP	.5624326	.1285136	4.38	0.000	.3099816	.8148837
_cons	-26.48501	4.27251	-6.20	0.000	-34.87789	-18.09213