
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мультиколлинеарность в моделях более чем с двумя объясняющими переменнымиСодержание книги
Поиск на нашем сайте
Предшествующее обсуждение мультиколлинеарности было ограничено случаем двух объясняющих переменных. В моделях с большим числом объясняющих переменных мультиколлинеарность также может быть вызвана приблизительно линейной взаимосвязью между ними. Может оказаться затруднительным различить воздействие одной переменной и линейной комбинации остальных переменных. В модели с двумя объясняющими переменными примерно линейная зависимость автоматически означает высокую корреляцию, но если их три или больше, то это не обязательно так. Линейная взаимосвязь не связана неизбежно с высокой коррелированностью любой пары из этих переменных. Последствия мультиколлинеарности здесь те же, что и в случае двух объясняющих переменных, и так же, как и в случае двух объясняющих переменных, данная проблема не будет серьезной, если теоретическая дисперсия случайного члена мала, число наблюдений велико и велики средние квадраты отклонений объясняющих переменных. Что можно предпринять в случае мультиколлинеарности? Различные методы, которые могут быть использованы для смягчения мультиколлинеарности, делятся на две категории: прямые попытки улучшить четыре условия, ответственные за надежность регрессионных оценок, и косвенные методы. Во-первых, можно попытаться уменьшить ơ2u. Случайный член отражает воздействие на переменную Y всех влияющих на нее переменных, не включенных непосредственно в уравнение регрессии. Если вы можете найти важную переменную, которая не включена в модель и, следовательно, вносит свои вклад в значение и, то вы уменьшите теоретическую дисперсию случайного: члена, добавив эту переменную в уравнение регрессии. Для иллюстрации мы возьмем функцию заработка, обсужденную в предыдущем разделе, где сильная корреляция между ЕХР, опытом работы и его квадратом EXPSQ. Мы теперь добавляем две новые переменные, которые часто считают важными факторами, влияющими на величину заработка: MALE, пол респондента; и ASVABC, составная переменная, основанная на тестах способности к познанию, разработанных для проверки профессиональной пригодности в вооруженных силах США. MALE является качественной переменной и методы работы с такими переменными будут обсуждены в гл. 5.
Результаты расширенной спецификации модели показаны в табл. 3.8. Все эти новые переменные имеют высокие значения t-статистик, и вследствие этого оценка а2и уменьшается с 166,51 до 155,53 (в верхней правой четверти распечатки результатов приведен ее расчет как частного от деления суммы квадратов остатков на число степеней свободы). Однако общий вклад новых переменных в объясняющую способность модели невелик, несмотря на их высокую значимость, и, как следствие, проблема мультиколлинеарности остается. Коэффициент при ЕХР все еще отрицателен, снижение стандартных ошибок коэффициентов ЕХР и EXPSQ мало. Заметим также, что стандартная ошибка коэффициента при S в действительности увеличилась. Это объясняется существенной корреляцией (коэффициент 0,58) между S и ASVABC. Это общая проблема для данного подхода при попытке уменьшить проблему мультиколлинеарности. Если новые переменные линейно связаны с одной или несколькими переменными, уже входящими в уравнение регрессии, то их включение может даже усилить проблему мультиколлинеарности. Следующий фактор для рассмотрения — число наблюдений п. Если вы работаете с данными перекрестной выборки (индивиды, домохозяйства, предприятия и т.д.) и готовитесь провести выборочный опрос, то можно увеличить размер выборки, затратив на это дополнительные средства. Можно сделать больше и при фиксированном бюджете, если Таблица 3.8 применить метод группировки. Вначале вы делите страну на географические части. Например, в США в опросе NLSY, из которого были взяты данные EAEF, страна была поделена на графства, отдельные города и стандартные столичные статистические зоны. Вы выбираете ряд географических частей случайным образом, возможно, используя внутригрупповые случайные выборки, чтобы обеспечить должное представительство столичных, прочих городских и сельских регионов. Далее вы проводите статистический опрос в выбранных зонах. Это сокращает затраты времени на поездки сотрудников, позволяя им опросить большее число респондентов. Если вы работаете с данными временных рядов, то может оказаться возможным увеличить выборку, перейдя к данным для более коротких временных интервалов, например к квартальным или даже месячным данным вместо годовых. Это настолько очевидная и простая вещь, что большинство исследователей, работающих с временными рядами, почти автоматически используют квартальные данные, если они имеются, вместо годовых данных (даже если проблема мультиколлинеарности не стоит) просто для того, чтобы минимизировать теоретические дисперсии коэффициентов регрессии. Здесь, однако, есть потенциальные проблемы. Вы можете внести или усилить автокорреляцию (см. гл. 12), но это можно нейтрализовать. Вы можете также внести или усилить смещение, вызванное ошибками измерения (см. гл. 8), если квартальные данные измерены менее аккуратно, чем соответствующие годовые данные. Эту проблему не так просто решить, но она может быть и не столь серьезной.
В табл. 3.9 представлен результат оценивания регрессии по всем 2714 наблюдениям совокупности данных EAEF. Сравнив этот результат с полученным по набору данных EAEF 21, мы видим, что стандартные ошибки здесь, как и ожидалось, оказались значительно меньше. Вследствие этого t-статистики S и новых переменных здесь значительно выше. Однако корреляция между ЕХР и EXPSQ — такая же высокая, как и в более малой выборке: увеличение размера выборки не было достаточно большим, чтобы оказать хоть какое-то влияние на проблему мультиколлинеарности. Коэффициенты при ЕХР и EXPSQ по-прежнему имеют не те знаки, которые мы ожидаем, потому что логично было думать, что коэффициент при ЕХР должен быть положительным, а коэффициент при EXPSQ — отрицательным, отражая убывающую отдачу. Коэффициент при EXPSQ имеет большую t-статистику, что должно нас беспокоить. Можно предположить, что это произошло случайно. Однако это может быть знаком того, что модель имеет неправильную спецификацию. Как мы увидим в последующих главах, существуют веские причины предполагать, что зависимая переменная в функции заработка должна быть скорее логарифмом заработка, чем его линейной формой. Таблица 3.9
Третий возможный путь смягчения проблемы мультиколлинеарности состоит в увеличении среднеквадратического отклонения объясняющих переменных. Это возможно лишь на стадии проектирования проводимого опроса. Например, при планировании проведения опроса домохозяйств для выяснения вопроса о влиянии уровня их дохода на структуру расходов необходимо путем группирования выборки обеспечить присутствие в ней относительно богатых и относительно бедных домохозяйств наряду с домохозяйствами со средним уровнем дохода. (Для ознакомления с теорией и методами построения выборок см., например, работы К. Мозера и Г. Калтона (Moser, Kalton, 1985 или Ф. Фоулера (Fowler, 1993)). Четвертый прямой метод является самым непосредственным из всех. Если вы еще находитесь на стадии планирования опроса, нужно приложить все усилия для получения такой выборки, в которой объясняющие переменные были бы как можно меньше связаны между собой (что, конечно, проще сказать, чем сделать). Далее, существуют также косвенные методы. Если коррелированные переменные связаны между собой концептуально, то может быть разумным объединить их в единый совокупный индекс. Это как раз то, что было сделано с тремя переменными уровня способностей ASVAB. Переменная ASVABC была рассчитана как взвешенное среднее переменных ASVAB02 (арифметические рассуждения), ASVAB03 (словарный запас), ASVAB04 (понимание смысла выражений). Три составляющие ASVABC высоко коррелированны между собой, комбинируя их, вместо использования по отдельности, нам удастся избежать появления возможной проблемы мультиколлинеарности. ASVAB02 имеет в двараза больший вес, чем две другие составляющие, поэтому численные и словесные элементы представлены в равных количествах, но такое решение является просто субъективным мнением о том, что кажется разумным предположить.
Еще одно возможное решение проблемы мультиколлинеарности состоит в том, чтобы убрать некоторые из коррелированных переменных, если их коэффициенты незначимы. Однако всегда есть опасность, что такие переменные на самом деле нужны в модели и что мультиколлинеарность вызывает незначимость их коэффициентов. Невключение переменных, которые должны быть в модели, может вызвать проблему смещения оценок при пропуске объясняющих переменных (см. гл. 6). Следующий способ смягчения проблемы мультиколлинеарности состоит в том, чтобы использовать внешнюю информацию, если она имеется, относительно коэффициента одной из переменных. Например, предположим, что известно, что совокупный спрос по одной из категорий расходов потребителя Y связан с совокупным располагаемым личным доходом Х ииндексом цен для данной категории Р:
Y= β1 + β2X + β3P + u (3.50)
Чтобы оценить модель этого вида, нужно использовать данные временного ряда. Если Х и Р имеют сильные временные тренды и поэтому высоко коррелированны, что часто имеет место с переменными, представляющими временные ряды, то мультиколлинеарность, вероятно, будет проблемой. Предположим, однако, что у нас есть также данные перекрестной выборки для Y и X, полученные из отдельного опроса домохозяйств. Эти переменные мы обозначим Y’ и Х’, чтобы показать, что представленные ими данные — не совокупные, а относятся к домохозяйствам. Предположив, что все домохозяйства в выборке платили примерно одну и ту же цену за данный товар, построим парную регрессию
Теперь подставим b'2 вместо β2 в модели с временными рядами
вычтем b2’X изобеих частей
и построим регрессионную зависимость величины Z= Y- b2’X отцены. Это — парная регрессия, так что мультиколлинеарность была устранена. Имеются две возможные проблемы с использованием этого метода, которые нужно иметь в виду. Во-первых, оценка β3 в (3.53) зависит от точности оценки b'2, которая, конечно, включает ошибку выборки. Во-вторых, вы предполагаете, что коэффициент переменной дохода имеет один и тот же смысл для временного ряда и перекрестной выборки, что может быть не так. Для многих предметов потребления краткосрочные и долгосрочные последствия изменений дохода могут различаться весьма заметно. Одна из причин — стандарты потребительских расходов подвержены инерции, которая может доминировать над эффектом изменения дохода в краткосрочном периоде. Другой фактор — то, что изменение дохода может затрагивать расходы как непосредственно, изменяя бюджетное ограничение, так и косвенно, через изменения в образе жизни, и косвенное влияние происходит намного медленнее, чем прямое. Как первое приближение, обычно считается, что регрессии на основе временных радов, особенно с короткими периодами выборки, оценивают краткосрочные воздействия, в то время как регрессии на основе перекрестных выборок оценивают воздействия долгосрочные. Для обсуждения этой и связанных с ней проблем см. работу Э. Ку и Дж. Мейера (Kuh, Meyer, 1957).
Наконец, еще один важный подход состоит в использовании теоретического ограничения, которое определяется как гипотетическое соотношение между параметрами модели регрессии. Это будет объяснено на примере модели продолжительности обучения. Предположим, мы выдвигаем гипотезу о том, что число завершенных лет обучения S зависит от ASVABC и от числа полных лет обучения матери и отца респондента (SM и SFсоответственно):
Оценив параметры модели на основе набора данных EAEF 21, получаем распечатку, представленную в табл. 3.10. Коэффициенты регрессии показывают, что S увеличивается на 0,13 года на каждый пункт увеличения ASVABC, на 0,05 года в расчете на каждый дополнительный завершенный год учебы матери и на 0,11 года в расчете на каждые дополнительный завершенный год учебы отца. Образование матери обычно считается, по крайней мере, столь же важным, если не более, чем образованна отца с точки зрения продолжительности обучения детей, так что относительно малое значение коэффициента при SM выглядит неожиданным. Также удивляет, что этот коэффициент незначим (даже на уровне значимости 5%) при использовании одностороннего теста. Однако формирование супружеских пар с близким уровнем образования ведет к высокой корреляции между SM и SF, и регрессия, очевидно, страдает от мультиколлинеарности. Предположим, что мы выдвигаем гипотезу о том, что образование матери и отца одинаково важны. Мы можем тогда наложить ограничение β3 = β4. Это позволяет нам записать уравнение как
При определении SР как суммы SM и SF уравнение может быть переписано с ASVABC и SP как объясняющими переменными:
Оценив параметры модели на основе набора данных EAEF21, получаем распечатку, представленную в табл. 3.11. Оценка β3 теперь равна 0,083. Неудивительно, что это значение — компромисс между коэффициентами при SM и SF, в предыдущей спецификации. Стандартная ошибка SP намного меньше, чем стандартные ошибки SM и SF, и это указывает на то, что использование ограничения привело к выигрышу в эффективности, и, как следствие этого,
Таблица 3.10
t-статистика очень высока. Таким образом, проблема мультиколлинеарности была здесь ограничена. Однако данное ограничение могло оказаться незначимым. Его нужно проверить с помощью теста. Мы увидим, как можно это сделать, в гл. 6. Таблица 3.11
3.5. Качество оценивания: коэффициент R2
Как и в парном регрессионном анализе, коэффициент детерминации определяет долю дисперсии Y, объясненную регрессией, и определяется как
а также как
или как квадрат коэффициента корреляции Y и
Далее, предположим, что вы оцениваете регрессию Y только на Х2, в результате получив следующее уравнение:
Это уравнение можно переписать:
Если сравнить уравнения (3.59) и (3.61), то коэффициенты в первом из них свободно определялись с помощью метода наименьших квадратов на основе данных для Y, Х2 и Х3 при обеспечении наилучшего качества оценки. Однако в уравнении (3.61) коэффициент Х был произвольно установлен равным нулю. Иоценивание не будет оптимальным, если только по случайному совпадение величина b3 не будет равна нулю, когда оценки будут такими же (в этом случае величина b* 1 будет равна Ь1, а величина Ь2* будет равна Ь2). Следовательно, обычно уровень коэффициента R2 будет выше в уравнении (3.59), чем в уравнении (3.61), и он никогда не станет ниже. Конечно, если новая переменная на самом деле не относится к этому уравнению, то увеличение коэффициента R2 будет, вероятно, незначительным. Вы можете решить, что поскольку коэффициент R2 измеряет долю дисперсии, совместно объясненной независимыми переменными, то можно определить отдельный вклад каждой независимой переменной и таким образом получить меру ее относительной важности. Это было бы очень удобно, если бы можно было так сделать. К сожалению, такое разложение невозможно, если независимые переменные коррелированны, поскольку их объясняющая способность будет перекрываться. Эта проблема рассматривается в разделе 6.2. F- тесты В разделе 2.11 F-тест использовался для проверки объясняющей способности модели парной регрессии:
где в качестве нулевой рассматривалась гипотеза Н0: β2 = 0, а в качестве альтернативной — гипотеза Н1: β2 ≠ 0. Нулевая гипотеза — та же самая, что и при выполнении t-теста для коэффициента наклона; выяснилось, что F-тест эквивалентен двустороннему t-тесту. Однако в случае множественной регрессии эти тесты выполняют разные функции: t-тесты проверяют значимость коэффициента при каждой переменной по отдельности, в то время как F'-тест проверяет их совместную объясняющую способность. Нулевая гипотеза, которую мы надеемся отвергнуть, заключается в том, что модель не обладает никакой объясняющей способностью. Модель не обладает объясняющей способностью, если выясняется, что Y не связана ни с одной из объясняющих переменных. Математически, следовательно, если модель имеет вид
то нулевая гипотеза для F-теста означает равенство всех коэффициентов β2,..., βk нулю:
H0:β2=…=βk=0 (3.64)
Альтернативная гипотеза Н1 заключается в том, что по крайней мере один из коэффициентов β2,..., βk отличен от нуля, F-статистика записывается как
и тест выполняется путем сравнения этой величины с критическим уровнем F, приведенным в столбце, соответствующем k-1 степеням свободы, и строке, соответствующей п - к степеням свободы, в соответствующей части табл. А.З в Приложении А. Данная F-статистика может быть также выражена в терминах R2 путем деления числителя и знаменателя в (3.65) на TSS, общую сумму квадратов отклонений, имея в виду, что ESS/TSS равно R2 и RSS/TSS равно (1 - R2):
Пример Иллюстрацией может служить модель продолжительности обучения. Предположим, что переменная S зависит от ASVABC, SM и SF:
Нулевая гипотеза для F-теста на общее качество уравнения состоит в том, что все три коэффициента наклона равны нулю:
H0: β2 = β3= β4=0 (3.68)
Альтернативная гипотеза состоит в том, что, по крайней мере, один из этих коэффициентов не равен нулю. В табл. 3.12 приведена распечатка результатом оценивания регрессии по набору данных EAEF21. В этом примере число объясняющих переменных к - 1 равно 3, и число степеней свободы п - к равно 536. Числитель F-статистики есть объясненная сумма квадратов отклонений, деленная на к- 1. В распечатке программы Stata эти числа (1181,4 и 3 соответственно) приведены в строке Model. Знаменатель здесь есть сумма квадратов остатков, деленная на остающееся число степеней свободы (2023,6 и 536 соответственно). Следовательно, F-статистика равна
как указано в распечатке. Все серьезные регрессионные пакеты рассчитывав эту F-статистику как один из элементов диагностической распечатки результатов оценивания. Критическое значение F(3; 536) не приведено в таблицах.F-распределения. но мы знаем, что оно должно быть меньше, чем F(3; 500), которое в этих таблицах приведено. При 0,1 %-ном уровне значимости оно равно 5,51. Следовательно, мы с уверенностью отвергаем Н0 на 0,1 %-ном уровне. Этот результат мол но было ожидать, поскольку как ASVABC, так и SF имеют высоко значимы: t-статистики. Поэтому мы знали заранее, что оба коэффициента β2 и β3 не равны нулю. Вообще говоря, F-статистика будет значимой, если значима по крайней мере одна из t-статистик. Однако в принципе F-статистика может и не быть значимой в этом случае. Предположим, что вы оценили не имеющую смысл регрессию с 40 объясняющими переменными, каждая из которых не является действительным детерминантом зависимой переменной. В этом случае F-ста тистика должна оказаться достаточно низкой, чтобы гипотеза Н0 не была отвергнута. Однако если вы выполните t-тесты для коэффициентов наклона на Таблица 3.12
5%-ном уровне, с 5%-ной вероятностью ошибки I рода, то в среднем можно ожидать, что 2 из 40 переменных будут иметь «значимые» коэффициенты. В то же время легко может случиться и так, что F-статистика будет значимой при незначимости всех t-статистик. Предположим, у вас имеется модель множественной регрессии, которая правильно специфицирована, и коэффициент детерминации R2 высок. Вероятно, в этом случае F-статистика высоко значима. Однако если объясняющие переменные сильно коррелированны и модель подвержена сильной мультиколлинеарности, то стандартные ошибки коэффициентов наклона могут оказаться столь велики, что ни одна из t-статистик не будет значима. В этом случае вы знаете, что ваша модель хороша, но у вас нет возможности выделить вклад каждой отдельно взятой переменной.
Дальнейший анализ дисперсии Помимо проверки уравнения в целом F-тест можно использовать для определения значимости совместного предельного вклада группы переменных. Предположим, что вы сначала оцениваете регрессию
где объясненная сумма квадратов отклонений составляет ESSk. затем вы добавляете еще (m - к) переменных и оцениваете регрессию
где объясненная сумма квадратов отклонений равна ESSm. Таким образом, вы объяснили дополнительную величину (ESSm - ESSk), использовав для этого дополнительные (m - к) степеней свободы, и требуется понять, превышает ли данное увеличение то, которое может быть получено случайно. Вновь используется F-тест, и соответствующая F-статистика может быть описана следующим образом:
Улучшение качества уравнения/Число использованных Необъясненная сумма квадратов отклонений/Оставшееся число степеней свободы (3.72)
Поскольку RSSm — необъясненная сумма квадратов отклонений в уравнении со всеми т переменными — равняется TSS-ESSm и RSSk — сумма квадратов отклонений в уравнении с к переменными — равняется TSS - ESSk, улучшение качества уравнения при добавлении (т - к) переменных, т.е. ESSm – ESSk, записывается выражением RSSk-RSSm. Следовательно, cсоответствующая F-статистика равна
При выполнении нулевой гипотезы о том, что дополнительные переменные не увеличивают объясняющей способности уравнения
H0: βk+1 = βk+2= …= βm=0 (3.74)
эта F'-статистика распределена с (т - к) и (п - т) степенями свободы. В верхней половине табл. 3.13 проведен дисперсионный анализ объясняющей способности первоначальных k - 1 переменных. В нижней половине таблицы это сделано для совместного предельного вклада новых переменных.
Пример Мы проиллюстрируем описанный тест с помощью функции продолжительности обучения. Таблица 3.14 показывает результат оценивания регрессии переменной S на ASVABC с использованием набора данных EAEF21. Заметим, что сумма квадратов отклонений равна здесь 2123,0. Таблица 3.13. Анализ дисперсии, исходные переменные и группа дополнительных переменных Сумма Степени Сумма квадратов, деленная квадратов свободы на число степеней свободы F-статистика
Объяснено исходными переменными ESSk k-1 ESSk/(k-1) RSSk/(k- 1) RSSk/(n-k) Остаток RSSk=TSS-ESSk n-k RSSk/(n-k)
Объяснено новыми переменными ESSm-ESSk = = RSSk-RSSm m-k (RSSk-RSSm) /(m-k) (RSSk-RSSm) /(m-k) RSSm/ (n-m)
Остаток RSSm=TSS-ESSm n-m RSSm/(n-m)
Таблица 3.14
Теперь добавим группу из двух переменных, представляющих завершенное число лет обучения каждого из родителей респондента (табл. 3.15). Вносят ли эти переменные совместно значимый вклад в объясняющую способность модели? Можно заметить, что t-тест показывает высокую значимость коэффициента при SF, но мы все же выполним и /F-тест. Заметим, что RSS- 2023,6. Улучшение качества регрессии после добавления «родительских» переменных представлено уменьшением суммы квадратов остатков, равным 2123,0 - 2023,6. Ценой этого является потеря двух степеней свободы, поскольку требуется оценить два дополнительных параметра. Сумма квадратов отклонений, остающаяся необъясненной после добавления SM и SF, равна 2023,6. Остающееся после добавления переменных число степеней свободы равно 540 - 4 = = 536. Отсюда
Таким образом, F-статистика равна 13,16. Критическое значение F(2; 500) на 0,1%-ном уровне равно 7,00. Критическое значение F(2; 536) должно быть еще меньше, и поэтому мы отвергаем H0 и делаем вывод о том, что переменные, отражающие уровень образования родителей респондента, имеют значимую совместную объясняющую способность. Таблица 3.15
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.118 (0.016 с.) |

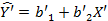 (3.51)
(3.51) (3.52)
(3.52) (3.53)
(3.53)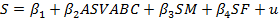 (3.54)
(3.54) (3.55)
(3.55) (3.56)
(3.56) (3.57)
(3.57) (3.58)
(3.58) . Этот коэффициент никогда не уменьшается (а обычно увеличивается) при добавлении еще одной переменной в уравнение регрессии, если все ранее включенные объясняющие переменные сохраняются. Для иллюстрации этого предположим, что вы оцениваете регрессию Y на Х2 и Х3 и получаете уравнение вида
. Этот коэффициент никогда не уменьшается (а обычно увеличивается) при добавлении еще одной переменной в уравнение регрессии, если все ранее включенные объясняющие переменные сохраняются. Для иллюстрации этого предположим, что вы оцениваете регрессию Y на Х2 и Х3 и получаете уравнение вида (3.59)
(3.59)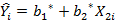 (3.60)
(3.60) (3.61)
(3.61) (3.62)
(3.62) (3.63)
(3.63) (3.65)
(3.65) (3.66)
(3.66) (3.69)
(3.69) (3.70)
(3.70)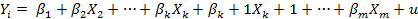 (3.71)
(3.71) (3.73)
(3.73) (3.75)
(3.75)


