
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение моделей Фридмена и БраунаСодержание книги
Поиск на нашем сайте
Несмотря на тот факт, что теоретические основы этих двух моделей совершенно различны (одна связана с будущим и ожиданиями, а другая — с прошлым и инерцией), модель Фридмена после преобразования Койка (11.39) и модель учета привычек (11.48) практически совпадают. Обе они включают краткосрочную и долгосрочную склонности к потреблению и скорость корректировки. Единственное различие в спецификации переменных — то, что в модели Брауна доход делится на заработную плату и прочий доход. Это полезное уточнение может быть сделано и в модели Фридмена. Сейчас это является стандартным свойством эмпирических моделей. В модели Фридмена нет постоянного члена, но это лишь небольшая эмпирическая деталь. В модели Фридмена случайный член отличается от случайного члена модели Брауна, и его структура может вызывать проблемы. Но, как будет показано в следующей главе, это различие не так уж существенно. Это пример проблемы наблюдаемо эквивалентных теорий, где для объяснения одних и тех же данных одинаковым образом могут быть использованы две или более теории, и между ними невозможно сделать выбор.
Предсказание Предположим, что вы оценили модель
на выборке из Т наблюдений временною ряда (t= 1,..., Т):
Имея некоторое послевыборочное значение переменной X, например ХT+р, вы можете предсказать соответствующее значение У:
Такие предсказания могут быть важными по двум причинам. Во-первых, вы можете быть одним из тех эконометристов, чья работа — заглядывать в экономическое будущее. Некоторые эконометристы изучают экономические закономерности с целью улучшить наше понимание того, как работает экономика, но для других это является лишь средством достижения более практичной цели — предвидеть, что может случиться. Во многих странах макроэкономическое прогнозирование имеет высокую репутацию, и коллективы эконометристов поддерживаются министерствами финансов или другими правительственными органами, частными финансовыми учреждениями, университетами и исследовательскими институтами, и их предсказания активно используются для формирования и обсуждения государственной политики или в деловых целях. Когда подобные предсказания публикуются в печати, они, как правило, привлекают гораздо больше внимания, чем большинство других видов экономического анализа, в основном благодаря своей сути и тому, что в отличие от большинства других видов экономического анализа они легко могут быть поняты средним гражданином. Даже человек с совершенно нематематическим и нетехническим складом ума в состоянии понять, что подразумевается под оценками будущего уровня безработицы, инфляции и т.д. Есть, однако, и другое применение эконометрического предсказания, которое делает его предметом заботы большинства эконометристов независимо от того, заняты они прогнозированием или нет. Оно дает метод оценки устойчивости регрессионной модели, который имеет большую исследовательскую направленность, чем диагностические статистики, использовавшиеся до сих пор. Прежде чем двигаться дальше, необходимо уточнить, что мы понимаем под предсказанием. К сожалению, в эконометрической литературе этот термин может иметь несколько различных значений, в соответствии с пониманием ХT+p в модели (11 52). Мы будем различать предсказания (ex post predictions) и прогнозы (forecasts). Это разделение сделано в соответствии с обычным использованием терминов, но, тем не менее, применяемая здесь терминология не вполне стандартная.
Предсказания Мы опишем Так, например, обращаясь снова к уравнению (3.39) модели связи общей инфляции и инфляции зарплаты, предположим, что для всего периода выборки мы оценили уравнение
где р и w — годовой уровень общей инфляции и инфляции зарплаты (в процентах) соответственно, и что мы знаем, что в один послевыборочный год уровень инфляции зарплаты составлял 6%. Тогда мы можем утверждать, что предсказанный уровень общей инфляции равен 5,8%. Мы, конечно, должны иметь возможность сразу сравнить его с действительным уровнем инфляции в этом году и рассчитать ошибку предсказания, которая равна разности между предсказанным и действительным значением В общем случае, если YT +р — действительное значение, а
Почему появляется ошибка предсказания? Это происходит по двум причинам. Во-первых, значение Пример Предположим, что, когда мы оценивали функцию спроса на жилье по набору данных для оценивания функций спроса, мы использовали лишь первое 41 наблюдение из выборки, т.е. данные за 1959—1999 гг., оставив последние четыре наблюдения для анализа предсказаний. Полученное на выборке 1959-1999 гг. уравнение выглядит следующим образом (в скобках приведены стандартные ошибки):
Значения LGHOUS для периода 2000—2003 гг., предсказанные с помощью этого уравнения, при использовании действительных значений личного располагаемого дохода и относительных цен жилья в эти годы, показаны в табл. 11.6 вместе с фактическими значениями этой переменной и ошибками предсказания. Предсказания, как и исходные данные, приведены в логарифмической шкале. Для удобства в табл. 11.6 показаны также абсолютные значения (в млрд. долл.) в ценах 2000 г., которые могут быть рассчитаны на основе логарифмических значений.
Таблица 11.6. Предсказанные и фактические расходы на жилье в 2000-2003 гг.
Мы можем видеть, что в этом случае предсказанные значения расходов на жилье превосходят фактические значения на 2,2—4,2%. Может ли такое предсказание считаться удовлетворительным? Мы обсудим эго в следующем разделе. Прогнозы Если вы хотите предсказать конкретное значение УT+p , не зная действительное значение ХT+p, то считается, что вы делаете прогноз (по крайней мере, если использовать терминологию этого текста). Макроэкономические предвидения, публикуемые в прессе, обычно являются в этом смысле прогнозами. Политиков, а в особенности широкую публику, мало интересуют «двусторонние» экономисты, рассуждения которых имеют вид «с одной стороны..., но если нет, то с другой стороны...». Обычно все желают точных однозначных оценок, дополненных, может быть, границами возможной ошибки, но часто даже и без этого. Прогнозы менее точны, чем предсказания, поскольку они подвержены воздействию дополнительного источника ошибки — предсказания значения ХT+p. Очевидно, что делающий прогноз эконометрист пытается, как правило, минимизировать эту дополнительную ошибку, моделируя как можно более точно поведение переменной X. Иногда для нее строят отдельную модель, иногда совмещают в одну модель уравнение для Y и уравнение для X, дополняя их множеством других соотношений и оценивая получающуюся систему одновременных уравнений (что рассматривалось в гл. 9).
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.007 с.) |

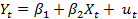 (11.50)
(11.50) (11.51)
(11.51) (11.52)
(11.52) как предсказание, если значение XT+p известно. Как это возможно? В общем случае эконометристы хотят включить все имеющиеся данные в свою выборку для максимизации ее размера и, как следствие, для минимизации дисперсии оценок, поэтому XT является последним зафиксированным значением X на момент оценки регрессии. Тем не менее, возможны две ситуации, когда ХT+p известны: когда вы ждете р или больше периодов после оценки регрессии или когда вы заранее ограничили период выборки так, чтобы у вас остались несколько последних наблюдений. Как мы увидим в следующем подразделе, весомой причиной так поступать может стать возможность без задержки оценить прогнозную точность модели.
как предсказание, если значение XT+p известно. Как это возможно? В общем случае эконометристы хотят включить все имеющиеся данные в свою выборку для максимизации ее размера и, как следствие, для минимизации дисперсии оценок, поэтому XT является последним зафиксированным значением X на момент оценки регрессии. Тем не менее, возможны две ситуации, когда ХT+p известны: когда вы ждете р или больше периодов после оценки регрессии или когда вы заранее ограничили период выборки так, чтобы у вас остались несколько последних наблюдений. Как мы увидим в следующем подразделе, весомой причиной так поступать может стать возможность без задержки оценить прогнозную точность модели. (11.53)
(11.53) - предсказываемое, то ошибка предсказания fT+p определяется как
- предсказываемое, то ошибка предсказания fT+p определяется как (11.54)
(11.54) (11.55)
(11.55)




