
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точность коэффициентов множественной регрессииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Далее мы рассмотрим факторы, определяющие ожидаемую точность коэффициентов регрессии для случая двух объясняющих переменных. Аналогичные рассуждения применимы и в более общем случае, но при более чем двух переменных необходим переход к матричной алгебре. Если истинная зависимость имеет вид: Yi= β1 + β2 X2i + β3 X3i+ui (3.29) и вы оценили уравнение регрессии Yi= b1 + b2 X2i + b3 X3i (3.30) использовав необходимые данные, то
где
где MSD(X2) — среднее квадратическое отклонение Х2, определяемое формулой Этому легко дать интуитивное объяснение. Чем выше корреляция, там сложнее определить влияние каждой из объясняющих переменных на Y и тем менее точными будут оценки коэффициентов регрессии. Это может стать серьезной проблемой, которую мы будем обсуждать в следующем подразделе. Стандартное отклонение распределения b2 представляет собой квадратный корень из дисперсии. Как и в случае парной регрессии, стандартная ошибки b2 — оценка стандартного отклонения. Оценим
где к — число параметров в уравнении регрессии. Тем не менее, мы можем получить несмещенную оценку
Стандартная ошибка представлена выражением
Факторы, определяющие стандартную ошибку, будут проиллюстрирован» путем сравнения их для функций заработка, оцененных для двух подмножеств респондентов в наборе данных EAEF 21, — тех, кто сообщил, что уровень ю заработной платы был установлен на основе переговоров о заключении коллективного трудового договора, и остальных. Результаты оценивания регрессии для этих двух подмножеств респондентов показаны в табл. 3.3 и 3.4. В программе Stata подмножества наблюдений могут быть определены путем добавления выражения «if» к соответствующей команде. Переменная COLLBARG длянашего набора данных равна единице для респондентов с коллективным договором и нулю — для остальных. Отметим, что при проверке выполнения равенства в программе Stata требуется повторить дважды знак равенства «=».
Стандартная ошибка коэффициента при S в первой регрессии равна 0,5493 что в два раза больше, чем во второй регрессии, — 0,2604. Далее мы рассмотрим причины этой разницы. Выражение (3.35) удобно переписать таким образом, чтобы был выделен вклад в него различных факторов:
Первый из необходимых нам элементов (su) может быть получен непосредственно из распечатки результатов оценивания регрессии. Величина
(Заметим, что Таблица 3.3
Таблица 3.4
Величина п - к дана справа от RSS, и отношение RSS/(n - к) — еще правее. Квадратный корень (su) обозначен как Root MSE («корень среднеквадтической ошибки») в верхней правой четверти распечатки результатов, это 12,577 — для регрессии по подвыборке с коллективным договором и 13,005 -для регрессии по подвыборке без коллективного договора. Число наблюдений — 101 для первой регрессии и 439 для второй — также приведено в верхней правой четверти распечатки результатов. Дисперсии S равные 6,2325 и 5,6, рассчитаны как квадраты стандартных отклонений, полученные при помощи команды «sum» в программе Stata, умноженные на (п - 1)/n. Коэффициенты корреляции между S и ASVABC, равные -0,4087 и -0,1784 соответственно, были рассчитаны с помощью команды «cor» программы Stata. На основе этого были рассчитаны множители из выражения для стандартной ошибки (3.36), которые показаны в нижней половине табл. 3.5. Можно заметить, что причина того, что стандартная ошибка коэффициента при 5 для подвыборки СВ относительно велика, состоит в том, что число наблюдений в этом подмножестве относительно мало. Больший коэффициент корреляции между S и ЕХР увеличивает разницу в результатах; в то время как меньшее значение su и большее значение MSD(S) уменьшает ее, но это достаточно незначительные множители. Таблица 3.5. Разложение стандартной ошибки коэффициента при S на составляющие su n MSD(S) rS,EXP со. Составляющая Коллективный договор 12,577 101 6,2325 -0,4087 0,5493 Нет коллективного договора 13,005 439 5,8666 -0,1784 0,2604 Множитель Коллективный договор 12,577 0,0995 0,4006 1,0957 0,5493 Нет коллективного договора 13,005 0,0477 0,4129 1,0163 0,2603
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.128.55 (0.011 с.) |

 — теоретическая дисперсия вероятностного распределения для b2 — будет описываться выражением:
— теоретическая дисперсия вероятностного распределения для b2 — будет описываться выражением: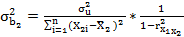 (3.31)
(3.31)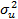 — теоретическая дисперсия величины u;
— теоретическая дисперсия величины u;  — коэффициент корреляции между Х1 и Х2 . Аналогичное выражение можно получить и для теоретической дисперсии величины b3 заменив
— коэффициент корреляции между Х1 и Х2 . Аналогичное выражение можно получить и для теоретической дисперсии величины b3 заменив  на
на  Записав (3.31) в виде:
Записав (3.31) в виде: (3.32)
(3.32)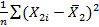 , мы можем увидеть, что так же, как и в случае парного регрессионного анализа, желательно, чтобы п и MSD(X2) были большими, а
, мы можем увидеть, что так же, как и в случае парного регрессионного анализа, желательно, чтобы п и MSD(X2) были большими, а  . Очевидно, что желательно иметь слабую корреляцию между Х2 и Х3.
. Очевидно, что желательно иметь слабую корреляцию между Х2 и Х3.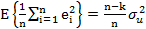 (3.33)
(3.33) , разделив на п-к, вместо п, таким образ ликвидировав смещение:
, разделив на п-к, вместо п, таким образ ликвидировав смещение: (3.34)
(3.34) (3.35)
(3.35) (3.36)
(3.36) (3.37)
(3.37) равняется нулю, что было доказано во Вставке 1.2 в гл. 1, и это доказательство легко можно обобщить.) Величина RSS приведена в верхней левой четверти распечатки результатов оценивания регрессии как часть разложения общей суммы квадратов отклонений на объясненную сумму квадратов отклонений (в распечатке программы Stata она обозначена как сумма квадратов отклонений модели {model sum of squares)) и остаточную сумму квадратов.
равняется нулю, что было доказано во Вставке 1.2 в гл. 1, и это доказательство легко можно обобщить.) Величина RSS приведена в верхней левой четверти распечатки результатов оценивания регрессии как часть разложения общей суммы квадратов отклонений на объясненную сумму квадратов отклонений (в распечатке программы Stata она обозначена как сумма квадратов отклонений модели {model sum of squares)) и остаточную сумму квадратов.


