Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства предсказаний, полученных с помощью МНКСодержание книги
Поиск на нашем сайте
В последующих рассуждениях мы сосредоточимся в основном на предсказаниях, а не на прогнозах, и обсудим свойства коэффициентов уравнения регрессии и свойства случайного члена, а не переменной X в случае, когда ее значения неизвестны. И в этом есть положительные моменты. Если значение YT+p порождается тем же процессом, что и выборочные значения переменной Y (т.е. в соответствии с уравнением (11.50), где uT+p удовлетворяет предпосылкам регрессионной модели, и если мы строим наше предсказание YT+p с помощью уравнения (11.52), то ошибка предсказания fT+p будет иметь нулевое математическое ожидание и минимальную дисперсию. Первое свойство легко продемонстрировать:
поскольку Е(b1) = β1, Е(b2)= β2 и Е(иT+р) = 0. Мы не будем доказывать свойство минимума дисперсии. Доказательство можно найти у Дж. Джонстона и Дж. Динардо (Jonston, Dinardo. 1997). Оба эти свойства сохраняются и для общего случая множественного регрессионного анализа. В случае уравнения парной регрессии теоретическая дисперсия fT+p определяется как
где Доверительные интервалы для предсказаний Мы можем получить значение стандартного отклонения для ошибки предсказания, если заменим
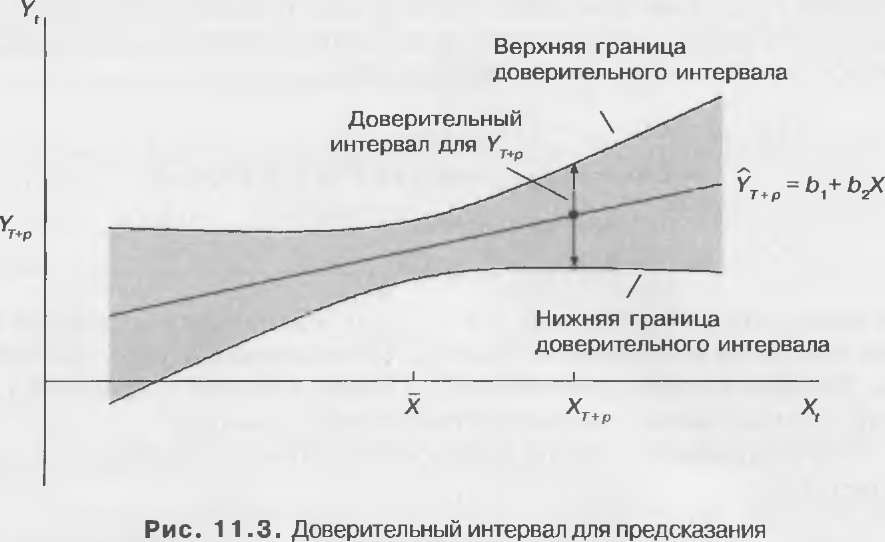
где tкрит — критическое значение t при заданных уровне значимости и числе степеней свободе, а с.о. — стандартная ошибка предсказания. На рис. 11.3 в общем виде показано соотношение между доверительным интервалом для предсказания и значением объясняющей переменной.
В уравнении множественной регрессии выражение, соответствующее (11.57), имеет гораздо более сложный вид, и оно лучше может быть представлено с помощью аппарата матричной алгебры. К счастью, имеется простой прием, который можно использовать для расчета значений стандартных ошибок при помощи компьютера. Обозначим период выборки как 1,..., Т, а период предсказания как T+1,..., T+Р. Вы оцениваете уравнение регрессии на выборке, совмещающей выборочный и прогнозный периоды, добавив (различные) фиктивные переменные для каждого из наблюдений периода предсказания. Это означает включение в модель набора фиктивных переменных DT+1, DT +2,..., DT+p где значение DT+p, равно нулю для всех наблюдений, кроме наблюдения Т + р, для которого оно равно единице. Как может быть показано, оценки коэффициентов при нефиктивных переменных и их стандартные отклонения будут в точности такими же, как и в уравнении регрессии, оцененном только на периоде выборки (см. работы Д. Салкевера (Salkever, 1976) и Ж.-М. Дюфора (Dufour, 1980)). Компьютер использует фиктивные переменные для получения точного соответствия в каждом наблюдении периода предсказания, и он делает это путем приравнивания коэффициента при фиктивной переменной к ошибке предсказания, определенной выше. Стандартная ошибка этого коэффициента равна стандартной ошибке предсказания. Пример В табл. 11.7 представлены результаты оценивания логарифмической регрессии расходов на жилье на показатели дохода и относительных цен, Таблица 11.7 Dependent Variable LGHOUS Method: Least Squares Sample: 1959 2003 Included observations 45
с фиктивными переменными D00—D03 для 2000—2003 гг. Коэффициенты при фиктивных переменных показывают ошибки предсказания, указанные в табл. 11.6. Предсказанный логарифм расходов на жилье в 2000 г в табл. 11.6 равняется 6,956. Из распечатки регрессии видно, что стандартная ошибка предсказания для этого года составляет 0,017. Для 38 степеней свободы критическое значение t-статистики при 5%-ном уровне значимости равно 2,024, и мы получаем следующий 95%-ный доверительный интервал предсказания для данного года: 6,956 - 2,024 х 0,017 < Y< 6,956 + 2,024 х 0,017, (11.59) то есть 6,922 < Y< 6,990. (11.60) Доверительный интервал не включает фактическое значение (6,914), и, таким образом, по крайней мере, для этого года предсказание оказалось неудовлетворительным. Очевидное объяснение этому состоит в том, что мы использовали очень простую статическую модель для оценки расходов на жилье. Как мы убедимся в следующей главе, динамическая модель является более предпочтительной. Тесты на устойчивость Тесты на устойчивость для регрессионной модели предназначены для оценки того, насколько поведение модели в послевыборочном периоде сравнимо с ее повелением в период выборки, на которой она была получена. В основании организации тестов на устойчивость могут лежать два принципа. Первый подход — сосредоточиться на предсказательной способности модели, второй подход — оценить, происходит ли сдвиг параметров в период предсказания.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.199 (0.008 с.) |



 (11.56)
(11.56) (11.57)
(11.57) и
и  – соответственно выборочное среднее значение и сумма квадратов отклонений переменной X. Из формулы следует, и это неудивительно, что чем больше значение X отклоняется от выборочного среднего, тем больше теоретическая дисперсия ошибки предсказания. Из формулы так же следует, и это вновь неудивительно, что чем больше объем выборки, тем меньше теоретическая дисперсия ошибки предсказания с нижним пределом, равным
– соответственно выборочное среднее значение и сумма квадратов отклонений переменной X. Из формулы следует, и это неудивительно, что чем больше значение X отклоняется от выборочного среднего, тем больше теоретическая дисперсия ошибки предсказания. Из формулы так же следует, и это вновь неудивительно, что чем больше объем выборки, тем меньше теоретическая дисперсия ошибки предсказания с нижним пределом, равным 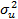 . С ростом объема выборки оценки b1, и b2 стремятся к истинным значениям соответствующих коэффициентов (в случае выполнения предпосылок модели), и единственным источником ошибки при предсказании будет случайный член uT+р, а он по определению имеет дисперсию
. С ростом объема выборки оценки b1, и b2 стремятся к истинным значениям соответствующих коэффициентов (в случае выполнения предпосылок модели), и единственным источником ошибки при предсказании будет случайный член uT+р, а он по определению имеет дисперсию  в уравнении (11.57) на
в уравнении (11.57) на  и извлечем квадратный корень. Тогда отношение величины (YT+p -
и извлечем квадратный корень. Тогда отношение величины (YT+p -  ) к стандартной ошибке при оценивании уравнения для периода выборки будет подчиняться t-распределению с числом степеней свободы (Т- к). Отсюда мы можем получить доверительный интервал для действительного значения YT+p:
) к стандартной ошибке при оценивании уравнения для периода выборки будет подчиняться t-распределению с числом степеней свободы (Т- к). Отсюда мы можем получить доверительный интервал для действительного значения YT+p: (11.58)
(11.58)