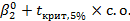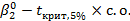Вставка 2.5. Описание результатов проверок по t-критерию

Предположим, что имеет место теоретическая зависимость

и нулевая и альтернативная гипотезы имеют вид H₀: β₂ = , H_1: β₂ ≠ . Если для β₂ по выборочным данным получена оценка b ₂, то области принятия и отклоне­ния гипотез для 5%- и 1%-ного уровней значимости могут быть в общем виде представлены левой частью рис. 2.9.

Правая часть рисунка показывает те же самые области для конкретного при­мера модели связи общей инфляции и инфляции, вызванной ростом заработ­ной платы; при этом нулевая гипотеза будет иметь вид β₂ = 1. Нулевая гипотеза не будет отклонена при уровне значимости 5%, если величина b_г находится в пределах 2,101 стандартной ошибки от единицы, т.е. в диапазоне 0,29-1,21, и она не будет отклонена при уровне значимости 1 %, если величина b₂ находится в пределах 2,878 стандартного отклонения от единицы, т.е. в диапазоне между 0,71 и 1,29.

Из рис. 2.9 можно видеть, что существует три типа зон принятия решений:

1) зона, где величина b₂ настолько далека от гипотетической величины (β ₂, что нулевая гипотеза отклоняется как при 5%~ном, так и при 1%-ном уровнях значимости;

2) зона, где величина b₂ достаточно далека от гипотетической величины (β ₂, чтобы нулевая гипотеза была отклонена при 5%-ном, но не при 1%-ном уровне значимости;

3) зона, где величина b₂ достаточно близка к гипотетической величине (β ₂, чтобы нулевая гипотеза не была отклонена ни при одном из двух рассматривае­мых уровней значимости.

На основании схемы можно проверить, что если нулевая гипотеза отклоня­ется при 1%-ном уровне значимости, то она автоматически отклоняется и при 5%-ном уровне значимости. Следовательно, в случае I необходимо заявить лишь об отклонении гипотезы при 1%-ном уровне. Заявлять об ее отклонении при 5%-ном уровне нет необходимости. Это равнозначно тому, чтобы сделать заявление о возможности взятия прыгуном высоты в 2 м, а затем, в качестве дополнения, заявить о его возможности взять высоту в 1,5 м. Аналогичным об­разом, для случая 3 вам необходимо сделать только заявление о том, что в этом конкретном случае гипотеза не будет отклонена при 5%-ном уровне значимо­сти. Отсюда автоматически следует, что она не будет отклонена и при 1%-ном уровне, и дополнение к этому заявлению имело бы тот же эффект, как если бы к заявлению о том, что прыгун в высоту не может взять высоту в 1,5 м, было до­бавлено утверждение о его неспособности взять высоту в 2 м. Лишь в случае 2 нужно (и желательно) представить результаты обеих проверок.

Заметим, что если вы обнаружили, что нулевую гипотезу можно отвергнуть при 5%г-ном уровне значимости, то не нужно на этом останавливаться. Вы обнаружили, что нулевая гипотеза может быть отвергнута при данном уровне значи­мости, но остается 5% шансов совершить ошибку I рода. Вы должны также вы­полнить тест при уровне значимости 1%. Если вы обнаружили, что нулевая ги­потеза может быть отвергнута и при этом уровне значимости, то это и есть результат, который нужно приставить. Риск ошибки I рода составляет теперь только 1%, и ваш вывод будет намного более убедительным. Это — случай 1, описанный выше. Если вы не можете отвергнуть гипотезу на 1%-ном уровне, то вы пришли к случаю 2 идолжны представить результаты обоих тестов.

 

а t-статистика вычисляется вручную. Например, вновь рассмотрим модель связи общей инфляции и инфляции, вызванной ростом заработной платы (2.61), и предположим, что выбранная модель оказалась следующей (в скоб­ах — стандартные ошибки):

(2.74)

(0.05) (0.10)

Если теперь исследовать гипотезу о том, что общая инфляция равна инфляции, вызванной ростом заработной платы, то наша нулевая гипотеза будет состоять в том, что коэффициент при w равен 1,0. Соответствующая t-статис­тика примет вид:

 

(2.75)

Если в выборке содержится, скажем, 20 наблюдений, то количество степе­ней свободы составит 18, а критическое значение для t на 5%-ном уровне зна­чимости составит 2,101. Абсолютная величина t-статистики меньше этого числа, поэтому в данном случае мы не отвергаем нулевую гипотезу. Оценка, равная 0,82, меньше гипотетического значения 1,00, но не настолько меньше, чтобы исключить возможность правильности нулевой гипотезы. И последнее замечание о представлении результатов оценивания регрессии: некоторые ав­торы помещают t-статистику в скобках под коэффициентом вместо стандарт ной ошибки. Это нужно тщательно проверять, а представляя свои результаты следует ясно указать, какую из двух величин вы приводите.

Общий случай	Решение	Пример зависимости общей инфляции и инфляции, вызван­ной ростом заработной платы
	Отклонить Н0 при уровне значимости 1% (как и при 5%)
		1,29
	Отклонить Н0 при уровне значимо­сти 5%, но не при 1%
		1,21
	При уровне значимости 5% или 1% гипотеза Н0 не отвергается	1,00
		0,79
	Отклонить Н0 при уровне значимости 5%, но не при 1%
		0,71
	Отклонить Н0 при уровне значимости 1% (как и при 5%)

 

Рисунок 2.9. Представление результатов проверки гипотез по f-критерию (суждения в скобках представлять не нужно)

Значения р

Пятый столбец результатов расчетов в табл. 2.6, озаглавленный Р >\t\, представляет альтернативный подход к описанию значимости коэффициентов регрессии. Числа в этом столбце показывают значения р для каждого коэффициента. Это вероятности получения соответствующих значений t-статистку если нулевая гипотеза Н₀: (β₂ = 0 верна. Значение p меньшее, чем 0,01, означает, что эта вероятность меньше, чем 1%, что, в свою очередь, означает, чтонулевая гипотеза была бы отклонена при 1%-ном уровне значимости; значение p между 0,01 и 0,05 означает, что нулевая гипотеза была бы отклонена при5%-ном уровне значимости, но не при 1%-ном. Величина p, равная или превышающая 0,05, свидетельствует, что нулевая гипотеза не была бы отклонена при 5%-ном уровне значимости.

Подход, основанный на значениях p более информативен, чем подход, основанный на задании с 5%- и 1%-ного уровня значимости, поскольку он дает точную вероятность ошибки I рода, если нулевая гипотеза верна. Например, в табл. 2.6 для функции заработка, приведенной выше, значение р для коэффициента наклона равно 0,0000, что означает, что вероятность получения t-статистики 10,59 или больше составляет здесь менее чем 0,005%. Следовательно мы отвергнем гипотезу о равенстве нулю коэффициента наклона при 1%-н: уровне значимости. В действительности мы отвергли бы здесь ее и при yровне значимости 0,1% (см. следующий подраздел). Выбор между подходом, основанным на значении р, и подходом с заданием уровня значимости 5%(1%) может быть основан на негласном соглашении. Так, в медицинской литературе используются значения p, в то время как в экономической литературе обычно применяются оценки 5%- и 1%-ного уровня значимости.