
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод и интерпретация коэффициентов множественной регрессииСодержание книги
Поиск на нашем сайте
Как и в случае парной регрессии, мы выбираем также значения коэффициентов регрессии, чтобы обеспечить наилучшее соответствие наблюдениям в надежде получить оптимальные оценки для неизвестных истинных значений параметров. Как и прежде, наше определение оптимальности соответствия определяется минимизацией RSS, т.е. суммы квадратов отклонений: RSS= где ei является остатком в наблюдении i, разницей между фактическим значением Yi в этом наблюдении и значением Yi прогнозируемым по уравнению регрессии: Yi = b1+ b2X2i + biX3i (3.4)
ei=Yi-Yi=Yi-bx-b2X2i-biX3i. (3.5) Отметим, что теперь переменные X имеют два нижних индекса. Первый означает номер переменной X, а второй относится к номеру наблюдения. Используя уравнение (3.5), мы можем записать:
RSS=
Вставка 3.1. Что случилось сХ1?Вы могли заметить, что переменная X отсутствует в общей модели регрессии Yi = β1+ β2X2i+…+ βkiXki + ui
Почему так? Причина здесь — в необходимости сделать обозначения аналогичными обозначениям в учебниках, использующих линейную (матричную) алгебру. В вашем следующем курсе эконометрики наверняка будет использоваться такой учебник. Для изложения с использованием линейной алгебры необходимо, чтобы каждый член в правой частиуравнения был произведением параметра и переменной. Если в модели есть постоянный член, как здесь, то можно исправить ситуацию, записав уравнение в виде: Yt = β1X1i+ β2X2i+ βk Xki+ ui где Х1i = I для всех наблюдений. При использовании обычной алгебры чаще всего нет необходимости вводить X1 в явной форме, и поэтому этой переменной нет. Единственный случай в этом учебнике, когда такая переменная может быть полезной, встретится при обсуждении «ловушки» фиктивных переменных в разделе 5.2.
Необходимые условия первого порядка для минимума, т.е.
Следовательно, мы имеем три уравнения с тремя неизвестными: b1 b2 и b3 . Первое уравнение можно легко перегруппировать для выражения величины b1 через b2 b3 и данные наблюдений для У, Х2 и Х3: bl= Используя это выражение и два других уравнения, путем некоторых преобразований можно получить следующее выражение для b2:
Аналогичное выражение для b3 можно получить путем перестановки Х2 и Х3 в уравнении (3.11). Цель данного анализа состоит в выделении двух основных моментов. Во-первых, принципы, лежащие в основе вычисления коэффициентов регрессии, в случаях множественной и парной регрессии не различаются. Во-вторых, сами выражения, тем не менее, различаются. Поэтому не следует пытаться использовать выражения, выведенные для парной регрессии, в случае множественной регрессии. Общая модель В предыдущем примере мы имели только две независимые переменных. В тех случаях, когда этих переменных больше двух, уже невозможно дать геометрическое представление того, что происходит, но развитие алгебраических выкладок в принципе вполне очевидно. Допустим, что переменная Y связана с к- 1 независимыми переменными Х2,...,Хк в соответствии с неизвестной истинной зависимостью. Мы предполагаем, что переменная Y зависит от к- 1объясняющих переменных Х2,..., Хк в соответствии с неизвестной истинной формулой: Yi=β1+β2X2i +…+ βkXki +ui, (3.12) Оценим уравнение для данного множества п наблюдений для Y, Х2,..., Хк методом наименьших квадратов:
Это вновь означает минимизацию суммы квадратов отклонений, а отклонение в наблюдении i выражается как ei=Yi- Уравнение (3.14) является обобщением уравнения (3.5). Теперь мы выбираем b1..., bk так, чтобы свести к минимуму RSS, сумму квадратов отклонений b1= Выражения для b2,..., bк становятся очень сложными, и математическая сторона не будет здесь представлена в явном виде. Расчеты здесь должны быть сделаны с помощью матричной алгебры.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.006 с.) |

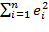 (3.3)
(3.3) (3.6)
(3.6) , дают следующие уравнения:
, дают следующие уравнения: (3.7)
(3.7)
 (3.8)
(3.8)
 (3.9)
(3.9) -b2
-b2  2-b3
2-b3  (3.11)
(3.11)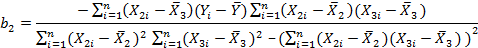
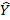 i=bi+b1Xli+...+bkXki. (3.13)
i=bi+b1Xli+...+bkXki. (3.13) . Мы получаем к условии первого порядка
. Мы получаем к условии первого порядка  …,
…,  , что дает к уравнений для нахождения к неизвестных. Можно легко показать, что первое из этих уравнений позволяет получить аналог уравнения (3.10), относящегося к случаю с двумя независимыми переменными:
, что дает к уравнений для нахождения к неизвестных. Можно легко показать, что первое из этих уравнений позволяет получить аналог уравнения (3.10), относящегося к случаю с двумя независимыми переменными:


