
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Два разложения для зависимой переменнойСодержание книги
Поиск на нашем сайте
На предшествующих страницах были рассмотрены два способа разложения величины зависимой переменной в регрессионной модели. Они будут использоваться далее во всей книге, и поэтому важно их правильное понимание и концептуальное разграничение. Первое из разложений связано с процессом, в соответствии с которым генерируются величины Y: Yi = β1 + β2Xi+ui (1.40) В наблюдении / величина Yi генерируется как сумма двух компонентов: нестохастического компонента β1 + β2Xi. и случайного члена иi. Это разложение — чисто теоретическое. Мы будем использовать его при анализе свойств оценок регрессии. Оно проиллюстрировано на рис. 1.7а, где QT— нестохастическая составляющая Y и PQ — случайный член. Другое разложение относится к линии регрессии:
Как только мы выбрали значения b 1 и b 2, каждая величина Y разлагается на расчетное (теоретическое) значение Ŷi и остаток еi Это разложение практически выполнимо, но оно в определенной степени произвольно, поскольку зависит
от нашего критерия для определения Ьх и Ь2, и на него неизбежно будут влиять конкретные значения случайного члена в наблюдениях выборки. Это показано на рис. 1.76, где RT— расчетное значение и PR — остаток.
Рисунок 1.7Ь. Разложение У на расчетное значение и остаток Интерпретация уравнения регрессии Существуют два этапа интерпретации уравнения регрессии. Первый этап состоит в словесном истолковании уравнения так, чтобы это было понятно человеку, не являющемуся специалистом в области эконометрики. На втором этапе необходимо решить, следует ли ограничиться этим или следует провести более детальное исследование зависимости. Оба этапа важны. Второй этап мы рассмотрим несколько позже, а пока обратим основное внимание на первый этап. Это будет проиллюстрировано на примере функции заработка, часового заработка в 2002 г. (EARNINGS), измеренного в долларах США, для которой строится регрессионная зависимость от продолжительности обучения S, определяемой как число завершенных лет обучения для 540 респондентов из Национального опроса молодежи в США (NLSY) в 1979 г. Эта база данных используется во многих других примерах и упражнениях книги. В Приложении В содержится ее описание. Приведенная ниже регрессия использует набор данных 21 из базы данных EAEF. В табл. 1.3 приведена распечатка результатов оценивания данной регрессии с помощью программы Stata. Соответствующая диаграмма рассеяния и линия регрессии показаны на рис. 1.8. На данном этапе игнорируйте все, кроме столбца с заголовком «coef.» в нижней половине таблицы. В нем показаны оценки коэффициента при переменной S и свободного члена, и, таким образом, имеем следующее оцененное уравнение:
EARNINGS = -13,93 + 2,46 S (1.42) Интерпретируя оцененное уравнение буквально, можно сказать, что коэффициент наклона показывает, что при увеличении S на одну единицу (измерения S) EARNINGS возрастает на 2,46 единиц (измерения EARNINGS). Поскольку S измеряется в годах, a EARNINGS измеряется в долларах в час, коэффициент при S показывает, что часовые заработки возрастают на 2,46 долл. на каждый дополнительный год учебы.
Что можно сказать о постоянном члене в уравнении? Формально говоря, он показывает прогнозируемый уровень EARNINGS при значении HGC, равном нулю. Иногда постоянный член имеет ясный смысл, иногда — нет. Если значения объясняющих переменных в выборке находятся достаточно далеко от нуля, то экстраполирование линии регрессии назад до нуля может породить проблемы. Даже если линия регрессии дает хорошее соответствие для наблюдаемой выборки, нет гарантии, что так же будет при экстраполяции влево или вправо. В данном случае буквальная интерпретация постоянного члена привела бы к бессмысленному выводу о том, что индивид с нулевым образованием имел бы часовой заработок в размере 13,93 долл. В нашем наборе данных никто из респондентов не имеет менее семи лет образования, поэтому неудивительно, что экстраполяция до нуля привела к проблемам.
Рисунок 1.8. Простейшая функция заработка
Вставка 1.1 дает общее руководство по интерпретации уравнения регрессии, когда переменные измерены в естественных единицах.
Вставка 1.1. Интерпретация линейного уравнения регрессии Представим простой способ интерпретации коэффициентов линейного уравнения регрессии:
если Y и X— переменные с простыми, естественными единицами измерения. Во-первых, мы можем сказать, что увеличение X на одну единицу (в единицах измерения переменной X) приведет к увеличению значения Y на b2 единиц (в единицах измерения переменной Y). Вторым шагом является проверка, каковы действительно единицы измерения X и Y, и замена слова «единица» фактической единицей измерения. Третьим шагом является проверка возможности более удобного представления результата без потери его сущности. Постоянная b} дает прогнозируемое значение У (в единицах У), если X равен нулю. Это может иметь или не иметь ясного смысла в зависимости от контекста. При интерпретации уравнения регрессии важно помнить о трех вещах. Во-первых, поскольку Ь1 есть всего лишь оценка Оценив регрессию, естественно задать вопрос о том, насколько аккуратными оказались наши оценки. Этот важный вопрос будет обсужден в следующей главе.
1.7. Качество оценивания: коэффициент R2 Цель регрессионного анализа состоит в объяснении поведения зависимой переменной Y. В любой данной выборке значение Y оказывается сравнительно низким в одних наблюдениях и сравнительно высоким — в других. Мы хотим знать, почему это так. Разброс значений Y в любой выборке можно суммарно описать с помощью∑ Выше было показано, что мы можем разбить значение Y в каждом наблюдении на две составляющие -
Это соотношение можно использовать для разложения ∑
На втором шаге мы использовали тот факт, что
Как показано во Вставке 1.2,∑ Yiei = 0 и ∑et =
Таким образом, имеем следующее разложение: TSS=ESS+RSS где TSS, общая сумма квадратов, дана в левой части уравнения, a ESS, «объясненная» сумма квадратов, и RSS, остаточная («необъясненная») сумма квадратов, представляют два слагаемых в его правой части. (Замечание: слова «объясненная» и «необъясненная» заключены в кавычки, поскольку объяснение может оказаться мнимым. Величина Сможет в действительности зависеть от некоторой другой переменной Z, а переменная X может служить в качестве замещающей переменной для Z (позже это будет пояснено более подробно). Было бы более правильно использовать выражение «видимое объяснение» вместо «объяснение».) Согласно (1.46),
Вставка1.2, Четыре полезных результата относительно регрессий, оцениваемых по обычному МНК: (1) Доказательство (1)
Откуда Разделив на n, получаем
Доказательство (2)
Однако Доказательство (3)
Финальный шаг использует уравнение (1.29.) Доказательство (4)
∑
Распечатка регрессионного анализа всегда включает R2 и может также содержать лежащий в его основе анализ дисперсии. Таблица 1.4 воспроизводит распечатку программы Stata для оценивания функции заработка, приведенной в табл. 1.3. Колонка с заголовком «SS», содержит суммы квадратов. Величина ESS, описываемая здесь как «моделируемая» (Model) сумма квадратов, равна 19322. Величина TSS (Total) равна 112010. Разделив ESS на TSS, получим, что R2 = 19322/112010 = 0,1725, что совпадает со значением R2, приведенным в правом верхнем углу таблицы. Низкое значение R2 частично объясняется тем фактом, что важные переменные, такие как опыт работы, не были учтены в модели. Оно также частично объясняется тем, что ненаблюдаемые характеристики оказывают большое влияние на заработок: R2 редко бывает выше 0,5, даже когда модель имеет хорошую спецификацию. Максимально возможное значение R2 равно единице. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что Yf — Yi для всех наблюдений и все остатки равны нулю. Тогда
При прочих равных условиях желательно, чтобы R2 был как можно больше. В частности, мы заинтересованы в таком выборе коэффициентов Ь1 и Ь2, чтобы максимизировать R2. Не противоречит ли это нашему критерию, в соответствии с которым Ь1 и Ь2 должны быть выбраны таким образом, чтобы минимизировать сумму квадратов остатков? Нет, легко показать, что эти критерии эквивалентны. На основе (1.46) мы можем записать R2 как
и, таким образом, те значения Ь1 и b2 которые минимизируют ∑ Заметим, что четыре полезных результата во Вставке 1.2 зависят от того, включается ли в модель постоянный член (см. упражнение 1.17). Если его нет, то разложение (1.46) неверно и два определения R2 в уравнениях (1.48) и (1.49) не эквивалентны. Любое определение R2 в этом случае может быть обманчивым, и к нему следует относиться с особой осторожностью.
Пример вычисления R2 Вычисление R2 выполняется на компьютере в рамках программы оценивания регрессии, поэтому данный пример приведен лишь в целях иллюстрации. Будем использовать простейший пример с тремя наблюдениями, описанный в разделе 1.3, где уравнение регрессии
построено по наблюдениям X и У, приведенным в табл. 1.5. В таблице также даны
Таблица 1.5. Анализ дисперсии в примере с тремя наблюдениями
Альтернативное представление R2 Интуитивно очевидно, что чем больше соответствие, обеспечиваемое уравнением регрессии, тем больше должен быть коэффициент корреляции для фактических и прогнозных значений Y, и наоборот. Покажем, что R2 фактически равен квадрату этого коэффициента корреляции, который мы который мы обозначим
Далее,
Во второй строке мы используем тот факт, что
2. СВОЙСТВА КОЭФФИЦИЕНТОВ РЕГРЕССИИ И ПРОВЕРКА ГИПОТЕЗ
С помощью регрессионного анализа мы можем получить оценки параметров зависимости. Однако они являются лишь оценками. Поэтому возникают вопросы о тоы насколько они надежны и каковы их свойства. Мы рассмотрим их в данной главе Способ рассмотрения этих вопросов и ответы на них зависят от предпосылок, которые делаются относительно регрессионной модели, а эти предпосылки, в свое очередь, зависят от природы используемых данных.
2.1. Типы данных и регрессионная модель Мы будем применять методы регрессионного анализа к данным трех видов: перекрестным выборкам, временным радам и панельным данным. Данные перекрестной выборки относятся к наблюдаемым объектам в одну и ту же единицу времени. Наблюдаемыми объектами могут быть индивиды, домохозяйства, предприятия, страны и множество других элементов, достаточно однородных по своей природе, чтобы использовать их для изучения предполагаемых зависимостей. Данные временного рада состоят из повторяющихся наблюдений одного и того же объекта, обычно с постоянным интервалом межл> наблюдениями. Примеры из области макроэкономики — квартальные данные по валовому внутреннему продукту, потреблению, денежной массе, процентным ставкам. Панельные данные, которые могут быть представлены как комбинация данных перекрестной выборки и временных рядов, состоят из повторяющихся наблюдений одних и тех же объектов во времени. Пример — данные Всеамериканского опроса молодежи {USNational Longitudinal Survey of Youth — NLSY), использованные для интерпретации регрессионной модели в разделе 1.6. Эти данные включают наблюдения над одними и теми же индивидами с 1979 г. до настоящего времени, которые до 1994 г. собирались ежегодно, а затем — раз в два года. Следуя подходу Р. Давидсона (Davidson, 2000), мы будем рассматривать три вида регрессионной модели. Модель А (для регрессий по данным перекрестных выборок): регрессоры (объясняющие переменные) являются нестохастическими, т.е. их значения в наблюдениях выборки не содержат стохастических (случайных) составляющих. Они будут рассмотрены далее во Вставке 2.1.
2.1. Нестохастические регрессоры В первой части пособия, мы полагаем, что регрессоры объясняющие переменные) в модели не содержат стохастических составляющих. Это делается для упрощения анализа. В действительности трудно себе представить реальные нестохастические переменные, кроме переменной времени, и поэтому нижеследующий пример выглядит несколько искусственным. Предположим, что мы связываем размер заработка с продолжительностью обучения S, определяемой как число полных лет обучения. Предположим, что из данных национальной переписи нам известно, что 1% населения имеет S= 8; 3% имеют S =9; 5% имеют S= 10; 7% имеют S= 11; 43% имеют S= 12 (что соответствует окончанию средней школы) и т.д. Предположим, что мы решили склать выборку размером в 1000 наблюдений, желательно — как можно более полно соответствующую генеральной совокупности. В этом случае мы можем сделать так называемую стратифицированную случайную выборку, включающую 10 индивидов с S = 8; 30 индивидов — с S = 9 и т.д. Значения S в такой выборке были бы предопределенными и, следовательно, нестохастическими. В больших выборках, полученных таким образом, чтобы они представляли население в целом, как, например, NLSY, вероятно, продолжительность обучения * другие демографические переменные достаточно полно соответствуют этому требованию. В гл. 8 мы признаем ограничивающий характер данной предпосылки и заменим ее на предпосылку о том, что значения регрессоров получены ж* заданных распределений. Модель В (также для регрессий по данным перекрестных выборок): значения регрессоров получены случайным образом и независимо друг от друга из заданных генеральных совокупностей. Модель С (для регрессий по данным временных рядов): значения регрессоров могут демонстрировать инерционность во времени. Смысл понятия -инерционный во времени» мы поясним в гл. 11—13 при рассмотрении регрессий по данным временных рядов. Регрессии с панельными данными могут рассматриваться как расширение модели В. Большая часть этой книги посвящена регрессиям по данным перекрестных выборок, т.е. моделям А и В. Причина этого заключается в том, что регрессии по данным временных рядов потенциально включают сложные технические аспекты, которых вначале лучше избежать. Начнем с модели А, исключительно для удобства анализа. Это позволит нам провести обсуждение регрессионного анализа в рамках довольно простой схемы, известной как классическая модель линейной регрессии. Мы заменим эту схему в гл. 8 более слабым и более реалистичным допущением, подходящим для регрессий по данным перекрестных выборок, о том, что переменные формируются как случайные выборки из заданных генеральных совокупностей. 2.2. Предпосылки регрессионной модели с нестохастическими регрессорами Для изучения свойств регрессионной модели необходимо ввести несколько предпосылок. В частности, для модели A будут введены следующие шесть предпосылок.
А. 1. Модель линейна по параметрам и правильно специфицирована
«Линейна по параметрам» означает, что каждый член правой части включает Р как простой множитель, и здесь нет встроенных зависимостей между βs. Примером модели, не являющейся линейной по параметрам, может служить модель
Мы отложим обсуждение аспектов, связанных с линейностью и нелинейностью, до гл. 4.
А.2. Объясняющая переменная в выборке имеет некоторую вариацию Очевидно, если величина X в выборке постоянна, то она не может объяснить какую-либо вариацию переменной Y. Если бы мы попытались оценить регрессию У на X при постоянной Xi мы бы обнаружили невозможность рассчитать коэффициенты регрессии. Величина Хi равнялась бы
были бы равны нулю. Если мы неспособны рассчитать b2 мы не сможем получить и b1
А.З. Математическое ожидание случайного члена равно нулю
E{ui) = 0 для всех i. (2.4) Мы предполагаем, что ожидаемое значение случайного члена должно равняться нулю в каждом наблюдении. Случайный член может оказаться и положительным, и отрицательным, но он не должен включать систематического смещения ни в одном из направлении. Действительно, если в регрессионное уравнение включен постоянный член, то обычно разумно считать, что это условие выполняется автоматически, поскольку функцией постоянного члена является отражение любой систематической постоянной части Y, не связанной с объясняющими переменными, включенными в уравнение регрессии. Чтобы сформулировать это математически, предположим, что наша регрессионная модель имеет вид
и E(ui)=µu (2.6) Определим
Vi=ui-µu (2.7)
Далее, используя (2.7) для замещения ui (2.5), имеем Yi=β1+ β2Xi+vi+µu= Где E(vi)=E(ui- Уплаченная цена заключается в изменении интерпретации постоянного члена. Он включил ненулевую составляющую случайного члена в дополнение ко всему тому, что отвечало за его формирование ранее. Обычно это не имеет значения, поскольку постоянный член в регрессионной модели редко представляет какой-либо интерес. Случайный член гомоскедастичен Мы предполагаем, что случайный член гомоскедастичен, т.е. что его значение в каждом наблюдении получено из распределения с постоянной теоретической дисперсией. На языке раздела, посвященного выборкам и оцениванию в главе «Обзор», это своего рода «предшествующее» понятие, когда мы задумываемся о потенциальном распределении случайного члена до того, как построена выборка. Когда выборка уже построена, случайный член окажется большим в одних наблюдениях и меньшим в других, но не должно быть причин, делающих его больше подверженным ошибке в одних наблюдениях по сравнению с другими. Если обозначить потенциальную дисперсию случайного члена в наблюдении как
Поскольку Е(ui) = 0, теоретическая дисперсия ui равна E(
Величина Если данная предпосылка не выполнена, оцененные по МНК коэффициенты оказываются неэффективными, и есть возможность получить более надежные оценки с помощью модифицированного метода оценивания. Это будет обсуждено в гл. 7. А 5. Значения случайного члена имеют взаимно независимые распределения ui распределен независимо от ui для всех j≠I (2.12) Мы предполагаем, что случайный член не подвержен автокорреляции, т.е отсутствует систематическая связь между его значениями в любых двух наблюдениях. Например, то, что случайный член в одном наблюдении велик и положителен, не должно быть фактором его большого положительного значения в следующем наблюдении (или большого отрицательного, малого положительного, или же малого и отрицательного). Значения случайного член* должны быть абсолютно независимыми между собой. Данная предпосылка означает, что
(Отметим, что обе теоретические средние Если данная предпосылка не выполняется, то МНК вновь дает неэффективные оценки. В гл. 12 обсуждаются возникающие при этом проблемы и пути их решения. Нарушения данной предпосылки для данных перекрестных выборок в любом случае редкие. С помощью этих предпосылок мы покажем в данной главе, что оценка МНК являются наилучшими линейными (относительно наблюдений У) несмещенными оценками (BLUE: best linear unbiased estimators) и что сумма квадратов отклонений, деленная на число степеней свободы, является несмещенной оценкой
А.6. Случайный член имеет нормальное распределение Обычно предполагают, что случайный член имеет нормальное распределение. Это распределение известно из курса статистики. Если величина и нормально распределена, то нормально распределены и коэффициенты регрессии. Это окажется для нас полезным далее в этой главе, когда мы приступим выполнению статистических t- и F-тестов для гипотез и к построению доверительных интервалов для β1 и β2 на основе результатов оценивания регрессий. Обоснование данной предпосылки связано с центральной предельной теоремой, описанной в главе «Обзор». Она говорит о том, что если случайная переменная представляет собой результат взаимодействия большого числа других случайных переменных, то она имеет приблизительно нормальное распределение, даже если ее составляющие такого распределения не имеют, при условии, что ни одна из них не доминирует. Случайный член и составлен из ряда факторов, не присутствующих явно в уравнении регрессии, и, таким образом, даже если мы ничего не знаем о распределении этих факторов (и даже о них самих), обычно есть основания предполагать нормальное распределение случайного члена.
Случайные составляющие коэффициентов регрессии Коэффициент регрессии, вычисленный методом наименьших квадратов, — особая форма случайной величины, свойства которой зависят от свойств случайного члена в уравнении. Мы продемонстрируем это сначала теоретически, а затем посредством контролируемого эксперимента. На протяжении всего рассмотрения мы будем иметь дело с моделью парной регрессии, в которой Y связан с нестохастической переменной X следующей зависимостью:
На основе п выборочных наблюдений будем оценивать уравнение регрессии
Во-первых, заметим, что Yi включает две составляющие. Она содержит неслучайную составляющую р^.), которая не имеет отношения к законам вероятности ф} и р2 могут быть неизвестными, но, тем не менее, это постоянные величины), и случайную составляющую иг Отсюда следует, что когда мы вычисляем Ь2 по обычной формуле
где b2 также содержит случайную составляющую. Если случайная составляющая принимает разные значения в п наблюдениях, то мы получаем разные значения Y и, следовательно, разные значения Теоретически мы можем разложить Ь2 на неслучайную и случайную составляющие. В соответствии с (2.14).
Следовательно, b2= Итак, мы показали, что коэффициент регрессии Ь2, полученный по любой выборке, состоит из двух слагаемых: 1) постоянной величины, равной истинному значению коэффициента
Таким образом, мы показали, что b2 равно истинному значению коэффициента жать проблемы, записав знаменатель как Отметим для проведения будущих выкладок три свойства коэффициентов аi:
Доказательства этих свойств приведены во Вставке 2.2. Подобным же образом можно показать, что Ь] включает постоянную составляющую, равную истинному значению Отметим, что практически выполнить эти разложения невозможно, поскольку истинные значения
Упражнение 2.1* Покажите, что b1= Вставка 2.2 Доказательства трех свойств коэффициентов ai
Докажем, что ∑ai=0
Поскольку
Используя
Докажем, что
Докажем, что
Вначале заметим, что
Поскольку
Эксперимент Монте-Карло По-видимому, никто точно не знает, почему эксперимент согласно методу Монте-Карло называется именно так. Возможно, это название имеет какое-то отношение к известному казино, как символу действия законов случайности. Объясним основное понятие посредством аналогии. Предположим, что собака обучена находить трюфели. Это дикорастущие земляные грибы, которые встречаются во Франции и Италии и считаются деликатесом. Они дороги, так как их трудно найти, и хорошая собака, обученная поиску трюфелей, стоит дорого. Проблема состоит в том, чтобы узнать, насколько хорошо собака ищет трюфели. Она может находить их время от времени, но, возможно также, что большое количество трюфелей она пропускает. В случае действительной заинтересованности вы могли бы выбрать участок земли, закопать трюфели в нескольких местах, отпустить собаку и посмотреть, сколько грибов она обнаружит. Посредством такого контролируемого эксперимента можно было бы непосредственно оценить уровень успешности поиска. Какое отношение это имеет к регрессионному анализу? Проблема в том, что мы никогда не знаем истинных значений
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.110 (0.014 с.) |

 (1.41)
(1.41)

 а Ь2 — оценка
а Ь2 — оценка  , интерпретация уравнения — также всего лишь оценка. Во-вторых, уравнение регрессии описывает лишь общую тенденцию в выборке. Каждый частный случай находится под влиянием случайных факторов. В-третьих, интерпретация основана на предположении, что уравнение правильно специфицировано. В действительности такая интерпретация функции заработка довольно наивна. Мы несколько раз вновь рассмотрим ее в последующих главах. Вам потребуется провести аналогичные эксперименты с использованием одного из других наборов данных EAEF, описанных в Приложении В.
, интерпретация уравнения — также всего лишь оценка. Во-вторых, уравнение регрессии описывает лишь общую тенденцию в выборке. Каждый частный случай находится под влиянием случайных факторов. В-третьих, интерпретация основана на предположении, что уравнение правильно специфицировано. В действительности такая интерпретация функции заработка довольно наивна. Мы несколько раз вновь рассмотрим ее в последующих главах. Вам потребуется провести аналогичные эксперименты с использованием одного из других наборов данных EAEF, описанных в Приложении В. , суммы квадратов отклонений от выборочного среднего. Мы должны уметь рассчитывать величину и структуру этой статистики.
, суммы квадратов отклонений от выборочного среднего. Мы должны уметь рассчитывать величину и структуру этой статистики. и
и 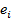 :
: (1.43)
(1.43) (1.44)
(1.44) = 0 и
= 0 и  = Y, продемонстрированный во Вставке 1.2. Следовательно,
= Y, продемонстрированный во Вставке 1.2. Следовательно,
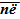 = 0. Следовательно,
= 0. Следовательно, =
= 
 это часть общей суммы квадратов, объясненной уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают как
это часть общей суммы квадратов, объясненной уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают как  :
: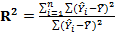
 =0, (2)
=0, (2)  ,(3)
,(3)  , (4)
, (4) 
 =
= 

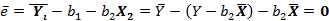

 =
= 
 =
=  -
-  -
-  =0
=0
 =0, так как
=0, так как  и ∑
и ∑  =0 из 3.
=0 из 3. , ∑
, ∑  =0 и управление является идеальным. Если в выборке отсутствует видимая связь между Y и X, то
=0 и управление является идеальным. Если в выборке отсутствует видимая связь между Y и X, то 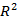 будет близок к нулю.
будет близок к нулю.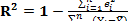
 , автоматически максимизируют R2.
, автоматически максимизируют R2.
 и ei для каждого наблюдения.
и ei для каждого наблюдения.  =4,6667,
=4,6667,  =4,5000 и ∑
=4,5000 и ∑  =0,1667. На основании этих значений мы можем вычислить R2, используя (1.48) или (1.49):
=0,1667. На основании этих значений мы можем вычислить R2, используя (1.48) или (1.49):
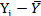





 :
: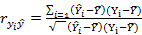 (1.53)
(1.53)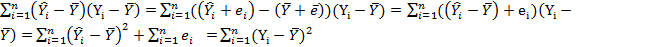 (1.54)
(1.54) = 0, а в четвертой мы использовали соотношение ∑
= 0, а в четвертой мы использовали соотношение ∑  =0, полученное во Вставке 1.2. В четвертой строке мы также использовали то, что ∑
=0, полученное во Вставке 1.2. В четвертой строке мы также использовали то, что ∑  =п
=п 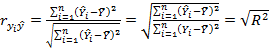
 (2.1)
(2.1) (2.2)
(2.2) для всех i, следовательно, и числитель, и знаменатель выражения
для всех i, следовательно, и числитель, и знаменатель выражения (2.3)
(2.3)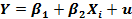 (2.5)
(2.5)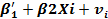 (2.8)
(2.8) Случайный член преобразованной модели уже удовлетворяет рассматриваемому требованию, поскольку
Случайный член преобразованной модели уже удовлетворяет рассматриваемому требованию, поскольку )=E(ui)-E(
)=E(ui)-E( 0 (2.9)
0 (2.9) , то данная предпосылка записывается как
, то данная предпосылка записывается как для всех i,
для всех i, ), и наше условие может быть также записано в форме
), и наше условие может быть также записано в форме
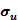 конечно, неизвестна. Одной из задач регрессионного анализ* является оценивание стандартного отклонения случайного члена.
конечно, неизвестна. Одной из задач регрессионного анализ* является оценивание стандартного отклонения случайного члена. — теоретическая ковариация между
— теоретическая ковариация между  и
и  . — равна нулю, поскольку
. — равна нулю, поскольку (2.13)
(2.13) и
и 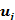 равны нулю в соответствие с предпосылкой (А.З) и что
равны нулю в соответствие с предпосылкой (А.З) и что  может быть разложено как Е(
может быть разложено как Е(
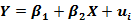 (2.14)
(2.14)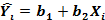
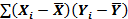 зависит от значений У, а значения Y— от значений и.
зависит от значений У, а значения Y— от значений и. и b2.
и b2.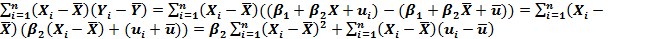 (2.17)
(2.17)
 , и 2) случайной составляющей, зависящей от случайного члена в выборке. Случайная составляющая определяет вариацию Ь2 вокруг постоянной составляющей
, и 2) случайной составляющей, зависящей от случайного члена в выборке. Случайная составляющая определяет вариацию Ь2 вокруг постоянной составляющей  (2.20)
(2.20)
 .Он по-прежнему означает то же самое. Мы могли бы избе-
.Он по-прежнему означает то же самое. Мы могли бы избе- , но это было бы неудобным.
, но это было бы неудобным. ,
,  и
и  (2.22)
(2.22) плюс случайную составляющую, являющуюся линейной комбинацией значений случайного члена. Мы предлагаем провести эти доказательства самостоятельно в качестве упражнения.
плюс случайную составляющую, являющуюся линейной комбинацией значений случайного члена. Мы предлагаем провести эти доказательства самостоятельно в качестве упражнения. , где сi=(1/n)-ai
, где сi=(1/n)-ai  , а определения выражаем (2.21)
, а определения выражаем (2.21)





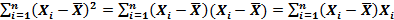 -
- 
 =0 (см. выше). Далее, используя предыдущие рассуждения в обратном порядке, запишем
=0 (см. выше). Далее, используя предыдущие рассуждения в обратном порядке, запишем



