
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Регрессия методом наименьших квадратовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
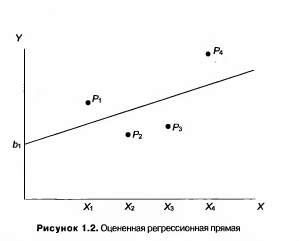
Допустим, что вы имеете четыре наблюдения для Х иY, представленные на рис. 1.1, и перед вами поставлена задача получить оценки значений β1и β2 в уравнении (1.1). В качестве грубой аппроксимации вы можете сделать это, отложив четыре точки Р и построив прямую, в наибольшей степени соответствующую этим точкам. Это сделано на рис. 1.2. Отрезок, отсекаемый прямой
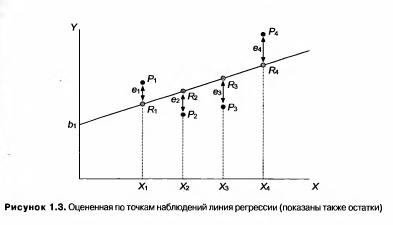
на оси Y, представляет собой оценку β1, он обозначен b1 а угловой коэффициент прямой представляет собой оценку коэффициента наклона β2, он обозначен как b2. Прямая, называемая оцениваемой моделью, описывается как Ŷi = b1+ b2Xi (1.2) где шляпка над Y означает, что это оцененное значение Y в зависимости от X, а не истинное его значение. На рис. 1.3 оцененные, или «теоретические», точки представлены как R1 - R4. С самого начала необходимо признать, что вы никогда не сможете определить истинные значения β1и β2 при попытке определить положение искомой прямой. Можно получить только оценки, и они могут быть хорошими или плохими. Иногда ваши оценки могут быть абсолютно точными, но это возможно лишь в результате случайного совпадения, и даже в этом случае у вас не будет способа узнать, что ваши оценки абсолютно точны.
Это справедливо и при использовании более совершенных методов. Построение линии регрессии на глаз является достаточно субъективным. Более того, как мы увидим в дальнейшем, оно просто невозможно, если переменная Y зависит не от одной, а от двух или более независимых переменных. Возникает вопрос: существует ли способ достаточно точной оценки β1и β2 алгебраическим путем? В качестве первого шага нужно определить, что понимается под остатком для каждого наблюдения. Это разность между действительной величиной Y в соответствующем наблюдении и расчетным значением по уравнению регрессии, то есть расстояние по вертикали между Рi и Ri в наблюдении i. Оно будет обозначаться как ei: ei = Yi - Ŷi (1.3) Остатки для четырех наблюдений показаны на рис. 1.3. Подставив (1.2) в (1.3), мы получим: ei = Yi – b1 – b2Xi (1.4) и, значит, остаток в каждом наблюдении зависит от нашего выбора значений b1 и b2. Очевидно, мы хотим построить линию регрессии, то есть выбрать значения b1 и b2 таким образом, чтобы эти остатки были минимальными. Очевидно также, что линия, хорошо соответствующая одним наблюдениям, не будет соответствовать другим, и наоборот. Необходимо выбрать какой-то критерий подбора, который будет одновременно учитывать величину всех остатков. Существует целый ряд возможных критериев, одни из которых работают лучше других. Например, бесполезно минимизировать сумму остатков. Сумма будет автоматически равна нулю, если вы сделаете b1 = Ý и b2 = 0, получив горизонтальную линию Y = Ý. В этом случае положительные остатки точно уравновесят отрицательные, но, несмотря на это, данная прямая не соответствует точкам наблюдений. Один из способов решения поставленной проблемы состоит в минимизации RSS (residual sum of squares), суммы квадратов остатков. Для рис. 1.3 справедлива формула: RSS= e12+e22+e32+e42 (1.5) В соответствии с этим критерием, чем меньше RSS, тем больше соответствие. Если RSS равно нулю, то получено абсолютно точное соответствие, так как это означает, что все остатки равны нулю. В этом случае линия будет проходить через все точки, однако, вообще говоря, это невозможно из-за наличия случайного члена. Существуют и другие достаточно разумные решения, однако при выполнении определенных условий метод наименьших квадратов дает несмещенные и эффективные оценки b1 и b2. По этой причине метод наименьших квадратов является наиболее популярным при использовании методов регрессионного анализа в относительно простых приложениях. В данной работе рассматривается обычный метод наименьших квадратов (МНК, или OLS — ordinary least squares). В последующих разделах будут рассмотрены другие его варианты, ко-е могут быть использованы для решения некоторых специальных проблем.
Регрессия методом наименьших квадратов Пример 1
Приведем действительно простой пример всего с двумя наблюдениями для того, чтобы продемонстрировать механику процесса: как показано на рис.1.4, наблюдаемое значение Y равно 3, когда Х равен 1; и Y= 5 при Х= 2. Предположим, что истинная модель имеет вид Yi = β1+ β2Xi + ui (1.6) и оценим коэффициенты b1 и b2 уравнения Ŷi =b1 + b2Xi (1.7) Очевидно, что при наличии всего двух наблюдений мы можем получить точное соответствие, проведя линию регрессии через две точки, однако сделаем вид, что мы этого не понимаем. Вместо этого придем к тому же выводу, используя метод рецессии. Если Х = 1, то Ý = (β1+ β2) в соответствии с уравнением регрессии. Если X=2, то Ý = (β1+ 2β2). Следовательно, мы можем сформировать табл. 1.1. Таким образом, остаток для первого наблюдения (е1), который задается выражением (Y1 - Ý 1), равен (3 - β1 - β2), и е2, заданный выражением (Y2- Ý 2), равен (5 - β1 -β2). Следовательно, RSS = (3 – b1 – b2)2 + (5 – b1 – 2b2)2 = 9 + b12 + b22 - 6b1 – 6b2 + 2b1b2 + 25 + b12 + 4b22 – 10b1 – 20b2 + 4b1b2 = 34 + 2b12 + 5b22 – 16b1 – 26b2 + 6b1b2 (1.8)
Теперь мы хотим выбрать такие значения b1 и b2 чтобы значение RSS было минимальным. Для этого мы используем дифференциальное исчисление и находим значения b1 и b2 удовлетворяющие следующим соотношениям:
Взяв частные производные, получаем
и
Таким образом, мы имеем
и
Решив эти два уравнения, получим b1 = 1 и b2 = 2, следовательно, уравнение регрессии будет иметь следующий вид:
Для того чтобы проверить, что мы пришли к правильному выводу, вычислим остатки:
Таким образом, оба остатка равны нулю, что означает, что линия проходит точно через обе точки. И это мы, разумеется, знали с самого начала. Пример 2 Используем пример, рассмотренный в предыдущем разделе, и добавим третье наблюдение: Y равен 6 при X = 3. Три наблюдения, показанные на рис.1.5, не лежат на одной прямой, поэтому точное соответствие получить
невозможно. В этом случае для вычисления положения прямой мы используем регрессию по методу наименьших квадратов. Начнем с задания стандартного уравнения
Для значений X, равных 1, 2 и 3, расчетные значения Y равны соответственно (
Следовательно,
Условия первого
Решая систему этих двух уравнений, получим b1 = 1,67 и b2 = 1,50. Следовательно, уравнение регрессии имеет следующий вид:
Три наблюдения и линия регрессии представлены на рис. 1.6.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.88.132 (0.007 с.) |



 и
и  (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11)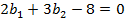 (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14) (1.15)
(1.15) (1.16)
(1.16)
 (1.17)
(1.17) ), (
), ( ) и (bl+3b2), они приведены в табл. 1.2.
) и (bl+3b2), они приведены в табл. 1.2.
 (1.18)
(1.18) (1.19)
(1.19) (1.20)
(1.20) (1.21)
(1.21)



