
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вставка 2.6. Терминология принятия (отклонения) гипотезыСодержание книги
Поиск на нашем сайте
В этом подразделе было показано, что следует отклонить нулевую гипотезу, если t-статистика больше, чем tкрит, или меньше, чем - tкрит, и не следует отклонять эту гипотезу, если t-статистика находится между t и t крит. Почему «не отклонять», к чему это усложнение? Не было бы проще сказать, что вы принимаете гипотезу, если абсолютная величина t -статистики меньше, чем tкрит. Аргументом против использования "термина «принять» является то, что вы способны «принять» несколько взаимоисключающих гипотез в одно и то же время. Так, в примере с зависимостью между общей инфляцией и инфляцией. вызванной ростом заработной платы, вй не могли бы отклонить нулевую гипотезуH0: β 2 = 0,9 или нулевую гипотезу H0: β 2 = 0,8. Логично утверждать, что вы не отклоняете эти нулевые гипотезы, а также нулевую гипотезу HQ; β 2 = 1, рассмотренную выше, но практически бессмысленно заявлять, что вы одновременно принимаете все три гипотезы. В следующем подразделе вы увидите, что можно определить целый ряд гипотез, которые не могут быть отклонены в результате данного эксперимента, поэтому было бы неосторожно выбрать одну из них как «принятую». Тесты с уровнем значимости 0,1% Если значение t-статистики очень велико, то следует проверить, отвергается ли нулевая гипотеза при уровне значимости 0,1%. Если возможно, следует представить результат такого теста, поскольку он дает возможность отвергнуть нулевую гипотезу с минимальным риском допущения ошибки I рода. Доверительные интервалы До сих пор мы предполагали, что гипотеза предшествует эмпирическим исследованиям. Однако это необязательно. Очень часто теория и эксперимент взаимодействуют, в этом отношении типичным примером является регрессия для функции заработка. Вначале мы оцениваем регрессию, потому что в соответствии с экономической теорией ожидаем, что продолжительность полученного образования влияет на заработок. Результат оценивания регрессии подтвердил это интуитивное ожидание в том смысле, что мы отвергли нулевую гипотезу β 2 = 0, но после этого возникло ощущение некоторой пустоты поскольку наша теория неспособна выдвинуть предположение о том, что значение (β 2 равняется некоторому конкретному числу. Теперь, однако, мы можем двинуться в противоположном направлении и задаться вопросом о том, какие гипотезы совместимы с результатом оценивания нашей регрессии.
Вполне очевидно, что гипотеза о том, что β 2 = 2,455, будет совместимой, так как гипотеза и результаты эксперимента совпадают. Кроме того, совместимыми будут и гипотезы о том, что β 2 = 2,454 и β2 = 2,456, так как разница между гипотезой и результатом эксперимента будет небольшой. Вопрос состоит в том, насколько сильно гипотетическое значение может отличаться от результата эксперимента, прежде чем они станут несовместимыми и мы должны будем отклонить нулевую гипотезу. Мы можем ответить на этот вопрос, используя предшествующие рассуждения. Из уравнения (2.72) мы можем видеть, что коэффициент регрессии b2 и гипотетическое значение β2 будут несовместимыми, если выполняются условия
т.е. если
что соответствует
Отсюда следует, что гипотетическое значение β2 является совместимым с результатом оценивания регрессии, если одновременно выполнены условия
т.е. если величина β2 удовлетворяет двойному неравенству
Любое гипотетическое значение для β2, которое удовлетворяет соотношению (2.80), будет автоматически совместимо с оценкой b 2, иными словами, не будет опровергаться ею. Множество всех этих значений, определенных как интервал между нижней и верхней границами неравенства, известно как доверительный интервал для величины β2. Отметим, что границы доверительного интервала одинаково отстоят от b 2. Отметим также, что так как значение tкрит зависит от выбора уровня значимости, границы будут также зависеть от этого выбора. Если принимается 5%-ный уровень значимости, то соответствующий доверительный интервал известен как 95%-ный интервал. Если выбирается 1%-ный уровень, то можно получить доверительный интервал с 99% и т.д. Так как t крит будет больше для 1%-ного уровня, чем для 5%-ного (при любом данном числе степеней свободы), то, следовательно, интервал в 99% будет шире интервала в 95%. Он включает все гипотетические значения для β2 в 95%-ном доверительном интервале, а также дополнительные промежутки с той и с другой стороны.
Вставка 2.7. Вторая интерпретаций доверительного интервала
Когда вы строите доверительный интервал, числа, которые вы определяете в качестве его верхнего и нижнего пределов, содержат случайные составляющие, которые зависят от значений случайного члена в наблюдениях выборки. Например, неравенство (2.80) включает верхний предел
Как b2, так и с.о.(b2) частично определяются значениями случайного члена. Мы надеемся, что доверительный интервал будет включать истинное значение параметра, но иногда он будет так искажен случайными факторами, что это будет не так. Какова же вероятность того, что доверительный интервал будет включать истинное значение параметра? Легко показать, используя элементарную теорию вероятности, что в случае 95%-ного доверительного интервала данная вероятность составляет 95% при условии, что модель правильно определена и что предпосылки, перечисленные в разделе 2.2 выполнены. Аналогичным образом, в случае 99%-ного доверительного интервала данная вероятность составляет 99%. Оцененный коэффициент (например, b2 в неравенстве (2.80)) обеспечивает точечную оценку рассматриваемого параметра, но при этом вероятность того, что истинное значение будет в точности равно этой оценке, ничтожно мала. Доверительный интервал дает так называемую «интервальную оценку» параметра, т.е. диапазон значений, который будет включать истинное значение с высокой > заранее определенной вероятностью. Именно эта интерпретация и дает название доверительному интервалу. (Более подробно этот вопрос рассматривается в работе Т. Уоннакотга и Р. Уоннакотта (Wannacott, Wannacott, 1990), гл. 8.)
Пример В распечатке для функции заработка, представленной в табл. 2.6, коэффициент при переменной S составил 2,455, его стандартная ошибка равнялась 0,232, а критическое значение t при 5%-ном уровне значимости — примерно 1,965. Отсюда соответствующий 95%-ный доверительный интервал составляет
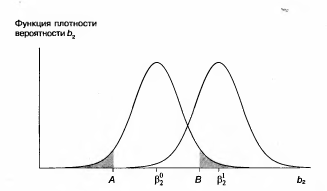
Иными словами, 1,999 < Поэтому мы отвергаем гипотетические значения только свыше 1,999 и ниже 2,911. Любые гипотетические значения внутри этих пределов не будут опровергаться полученным результатом регрессии. Доверительный интервал показан в последнем столбце распечатки программы Stata. Это, однако, не является стандартным свойством регрессионных пакетов, и обычно приходится рассчитывать интервал самостоятельно. Односторонние t-критерии В нашем обсуждении t-критериев мы начали с нулевой гипотезы Н0: H0: В этом случае по каким-то причинам существуют только два возможных истинных значения коэффициента при X, равных Предположим, что мы хотим проверить гипотезу Н0 при 5%-ном уровне значимости и используем для этого обычную процедуру, которая уже рассматривалась в этой главе. Мы находим границы для верхнего и нижнего 2,5%-ных «хвостов» t-распределения, считая, что Н0 верна, обозначив их как А и В на рис. 2.10, и гипотеза H0 отклоняется, если коэффициент регрессии b2 оказывается левее точки А или правее точки В. Далее, если значение b2 находится справа от 5, то оно намного лучше совместимо с гипотезой H1 чем с гипотезой H0; вероятность его нахождения справа от В, если истинна H1 намного больше, чем при истинности гипотезы H0. Здесь у нас не должно быть сомнений в том, чтобы отклонить гипотезу Н0. Следовательно, мы делаем вывод, что гипотеза H1 верна.
Если, однако, b2 находится слева от А, то используемая процедура проверки приведет нас к неверному заключению. Последняя требует отклонить гипотезу H0 и, следовательно, принять гипотезу H1 несмотря на то, что при истинности гипотезы Н1 вероятность нахождения b2 слева от А ничтожно мала. Мы даже не построили график функции плотности вероятности, соответствующей гипотезе Н1. Если такое значение b2 получается только раз на миллион случаев при истинности H1 но в 2,5% случаев при истинности H0, то здесь намного логичнее считать, что истинной является гипотеза Н0. Конечно, в од-
Рисунок 2.10. Распределение величины b2 в соответствии с гипотезами Н0 и Н 1 ном случае на миллион вы сделаете ошибку, но в остальных случаях вы будете правы. Следовательно, мы будем отклонять H0, только если b2 оказывается на верхнем 2,5%-ном «хвосте» распределения, т.е. справа от В. Это означает, что теперь мы выполняем проверку гипотезы с односторонним критерием, сократив в результате вероятность допустить ошибку I рода до 2,5%. Поскольку уровень значимости определен как вероятность допустить ошибку I рода, то он теперь также составляет 2,5%. Как уже отмечалось, экономисты обычно предпочитают проверку гипотез с 5%- и 1%-ным уровнями значимости проверкам с 2,5%-ным уровнем значимости. Если вы хотите провести проверку с 5%-ным уровнем значимости, то вы должны переместить точку В влево так, чтобы получить 5% вероятности в «хвосте» распределения и увеличить вероятность допустить ошибку I рода до 5%. (Вопрос: Почему намеренно выбирается увеличение вероятности допустить ошибку I рода? Ответ: потому что одновременно сокращается вероятность допустить ошибку II рода, т.е. вероятность того, что нулевая гипотеза не будет отклонена, когда она является ложной. В большинстве случаев нулевая гипотеза состоит в том, что соответствующий коэффициент равен нулю, и вы пытаетесь опровергнуть это, показав, что рассматриваемая переменная действительно имеет влияние. В такой ситуации при выборе одностороннего критерия вы уменьшаете риск не отвергнуть ложную нулевую гипотезу, в то время как вероятность ошибки I рода сохраняется на 5%-ном уровне.)
Если стандартное отклонение величины b2 известно (что практически маловероятно), а распределение нормально, то точка В будет находиться в z стандартных отклонениях вправо от Аналогично, если вы хотите выполнить проверку с уровнем значимости 1%, то вы перемещаете В вправо до той точки, где «хвост» распределения со-
держит 1% вероятности. Если вам пришлось вычислить стандартную ошибку величины b2 на основе выборочных данных, то нужно найти критическое значение для t вколонке, соответствующей 1%. В проведенном обсуждении мы допустили, что Мощность критерия В данном конкретном случае мы можем вычислить вероятность допустить ошибку II рода, т.е. принять ложную гипотезу. Предположим, что мы приняли ложную гипотезу H0: Используя односторонний критерий вместо двустороннего, можно получить большую мощность для любого уровня значимости. Как мы уже видели, при переходе к одностороннему критерию с 5%-ным уровнем значимости точка В на рисунке сдвигается влево и, тем самым, снижается вероятность принятия гипотезы H0, если она ложна. H0:
Мы рассмотрели случай, когда альтернативная гипотеза включала конкретное гипотетическое значение Рисунок 2.11. Вероятность не отвергнуть гипотезу Н0, если она ложна (двусторонний тест)
Мы по-прежнему хотели бы исключить левый «хвост» распределения изобласти непринятия гипотезы, так как низкое значение для b2 более вероятно получить при гипотезе H0: H0:
Аналогичным образом, если альтернативная гипотеза имеет вид Н1:
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.199 (0.014 с.) |

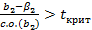 или
или 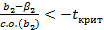 (2.76)
(2.76)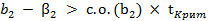 или
или 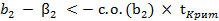 (2.77)
(2.77)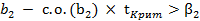 или
или 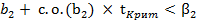 (2.78)
(2.78) и
и 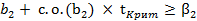 (2.79)
(2.79) (2.80)
(2.80)
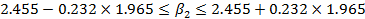 (2.81)
(2.81)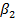 < 2,911. (2.82)
< 2,911. (2.82)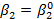 и провели проверку возможности ее отклонения при коэффициенте регрессии, равном b2. Если бы мы отклонили эту гипотезу, то косвенно приняли бы альтернативную гипотезу Н1:
и провели проверку возможности ее отклонения при коэффициенте регрессии, равном b2. Если бы мы отклонили эту гипотезу, то косвенно приняли бы альтернативную гипотезу Н1:  . До сих пор альтернативная гипотеза была лишь простым отрицанием нулевой гипотезы. Если, однако, мы можем сформулировать альтернативную гипотезу более конкретно, то мы должны и усовершенствовать процедуру проверки. Проведем исследование трех случаев: первый случай — весьма частный, когда существует единственное альтернативное истинное значение
. До сих пор альтернативная гипотеза была лишь простым отрицанием нулевой гипотезы. Если, однако, мы можем сформулировать альтернативную гипотезу более конкретно, то мы должны и усовершенствовать процедуру проверки. Проведем исследование трех случаев: первый случай — весьма частный, когда существует единственное альтернативное истинное значение 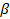 2, которое мы обозначим
2, которое мы обозначим 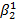 ; второй случай — если
; второй случай — если  , то оно должно быть больше
, то оно должно быть больше  .
.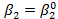 , H1:
, H1: 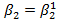
 , H1:
, H1: 
 , без указания какого-либо конкретного значения.
, без указания какого-либо конкретного значения.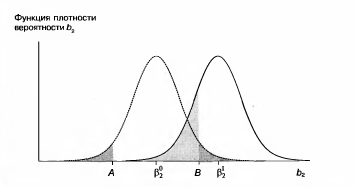 113
113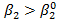 , а следовательно, это будет свидетельствовать в пользу гипотезы H0, а не против нее.Поэтому мы вновь предпочтем односторонний критерий проверки гипотезы двустороннему, рассматривая правый «хвост» распределения как область непринятия гипотезы. Отметим, что, так как
, а следовательно, это будет свидетельствовать в пользу гипотезы H0, а не против нее.Поэтому мы вновь предпочтем односторонний критерий проверки гипотезы двустороннему, рассматривая правый «хвост» распределения как область непринятия гипотезы. Отметим, что, так как 
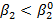 то мы предпочтем проверку, основанную на одностороннем критерии, использующем левый «хвост» распределения в качестве области отклонения гипотезы.
то мы предпочтем проверку, основанную на одностороннем критерии, использующем левый «хвост» распределения в качестве области отклонения гипотезы.


