
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прикладная эконометрика в предпринимательствеСодержание книги
Поиск на нашем сайте
Прикладная эконометрика в предпринимательстве Часть I Учебное пособие для второй ступени высшего образования по специальности: 1-26 81 03 Управление недвижимостью
СОДЕРЖАНИЕ
Введение УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИНЫ…………………….…………………………….4 1. ПАРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ …………………………….……………………9 2. СВОЙСТВА КОЭФФИЦИЕНТОВ РЕГРЕССИИ И ПРОВЕРКА ГИПОТЕЗ ………….…47 3. МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ ………………………………….…72 4. МОДЕЛИРОВАНИЕ И СВОЙСТВА РЕГРЕССИОННЫХ МОДЕЛЕЙ С ВРЕМЕННЫМИ РЯДАМИ ……………………………………………….…………….………………………….93 5. ПРЕОБРАЗОВАНИЯ И СПЕЦИФИКАЦИЯ ПЕРЕМЕННЫХ РЕГРЕССИИ 6. ОЦЕНИВАНИЕ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ 7. НЕСТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ 8. МОДЕЛИ С ПАНЕЛЬНЫМИ ДАННЫМИ Перечень рекомендуемой литературы…………………………………………………….…..99
ПРИЛОЖЕНИЕ. Пример подготовки исследовательского проекта ………………….…….100
Введение В данной дисциплине изучается построение эконометрических моделей, возможности их использования для описания, анализа и прогнозирования реальных экономических задач, связанных с предпринимательской деятельностью. Современные требования к уровню экономического образования предполагают у обучаемых наличие широких математических и статистических знаний, необходимых при решении задач, связанных с использованием моделирования и количественного анализа экономических процессов. Математическая подготовка обычно охватывает математический анализ, методы линейной и нелинейной оптимизации, использование логарифмов и показательных функций, умение работать с формулами, уравнениями и графиками. В статистическую подготовку необходимо включать знакомство со статистическими распределениями, умение измерять основные статистические параметры – среднее значение, стандартное отклонение и коэффициенты корреляций, знание методов регрессионного и корреляционного анализа, методов дисперсионного, факторного и дискриминантного анализа и условия их применения. Дисциплина предусматривает изучение прикладного эконометрического анализа и получение навыков использования знаний по следующим вопросам: линейная модель множественной регрессии; метод наименьших квадратов (МНК); свойства оценок МНК; показатели качества регрессии; линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками; обобщенный метод наименьших квадратов (ОМНК); регрессионные модели с переменной структурой (фиктивные переменные); нелинейные модели регрессии и их линеаризация; характеристики временных рядов; модели стационарных и нестационарных временных рядов, их идентификация; система линейных одновременных уравнений; методы анализа панельных данных.
УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИНЫ ХАРАКТЕРИСТИКА ДИСЦИПЛИНЫ Связь с другими дисциплинами учебного плана Дисциплина «Прикладная эконометрика в предпринимательстве» основана на использования знаний, полученных студентами по высшей математике, микроэкономике, экономике организации (предприятия). В свою очередь, данная дисциплина позволяет получить знания, которые должны стать информационно-методической базой в процессе изучения некоторых дисциплин специализации, например, таких как, «Планирование, организация и управление производством», «Управление недвижимостью» и других. Цели и задачи дисциплины Цель дисциплины – получить глубокие знания и сформировать целостное представление о прикладном эконометрическом анализе в сфере бизнеса, сформировать понимание и умение применять основных эконометрических моделей и методов, умение обосновывать управленческие решения, с использованием результатов эконометрического анализа. Предмет дисциплины – эконометрические методы анализа, построения моделей и оценки их качества. Объект изучения – экономические явления и процессы в предпринимательстве. Основная задача дисциплины – помочь студентам в обучении построению эконометрических моделей, оценке качества моделей, прогнозированию с помощью эконометрических моделей с целью обоснования принимаемых решений, в том числе и в области управления недвижимостью. Место дисциплины в подготовке специалиста Дисциплина «Прикладная эконометрика в предпринимательстве» – одна из важнейших дисциплин, успешное освоение которой помогает решению профессиональных задач. Дисциплина отвечает профилю подготовки на второй ступени высшего образования по специальности «Управление недвижимостью». Особенностью дисциплины является применение современных прикладных программных продуктов для анализа и использование реальных статистических данных, активное использование информации из глобальных компьютерных сетей. Для изучения дисциплины студенты должны владеть следующими навыками: иметь навыки сбора и подготовки информации; иметь навыки работы с прикладными статистическими пакетами; владеть базовыми математическими и статистическими навыками. В процессе изучения данной дисциплины решаются общеобразовательные, практические и теоретические задачи. Требования к освоению дисциплины В результате изучения данной дисциплины студенты должны: знать: - элементы и основные составляющие современное понятие математической статистики; - основные методологические подходы и приемы изучения экономических процессов; - методы статистического анализа; - степень и характер влияния отдельных факторов на экономические показатели. понимать: - основные статистические инструменты, методы и способы их обработки и реализации. - принципы количественного анализа реальных экономических процессов и явлений во времени и в пространстве; уметь: - применять общие и специальные методы экономических и статистических расчетов, - владеть методикой сбора, обработки экономической информации и прогнозировать состояние и развитие экономических процессов. владеть: - знаниями по эмпирическому выводу экономических зависимостей, закономерностей и законов, действующих в настоящее время; - навыками строить и использовать эконометрические модели, а также оценивать их параметры для объяснения поведения исследуемых экономических явлений; - проверять выдвигаемые гипотезы о свойствах экономических показателей и формах их связи; - научиться оценивать и использовать результаты эконометрического анализа для прогноза и принятия обоснованных экономических решений.
ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Тема 1. Предмет дисциплины «прикладная эконометрика в предпринимательстве». Цель, задачи и методы, используемые при ее изучении Предмет и задачи курса. Место дисциплины «Прикладная эконометрика в предпринимательстве» в системе изучаемых дисциплин. Краткая характеристика и логика построения и состава курса, основные рассматриваемые вопросы. Форма контроля освоения курса и приобретения знаний. История создания и развития эконометрики. Основные понятия и особенности эконометрического метода. Связь эконометрики с другими дисциплинами.
Тема 2. Парный регрессионный анализ Модель парной линейной регрессии. Регрессия методом наименьших квадратов. Примеры регрессии методом наименьших квадратов. Регрессия методом наименьших квадратов с одной независимой переменной. Два разложения для зависимой переменной. Интерпретация уравнения регрессии. Качество оценивания. ПАРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ В главе показано, как, используя соответствующие данные, можно получить количественное выражение гипотетического линейного соотношения между двумя переменными. В главе объясняется важный принцип регрессионного анализа — метод наименьших квадратов, а также выводятся формулы, выражающие коэффициенты регрессии. Пример 1
Приведем действительно простой пример всего с двумя наблюдениями для того, чтобы продемонстрировать механику процесса: как показано на рис.1.4, наблюдаемое значение Y равно 3, когда Х равен 1; и Y= 5 при Х= 2. Предположим, что истинная модель имеет вид Yi = β1+ β2Xi + ui (1.6) и оценим коэффициенты b1 и b2 уравнения Ŷi =b1 + b2Xi (1.7) Очевидно, что при наличии всего двух наблюдений мы можем получить точное соответствие, проведя линию регрессии через две точки, однако сделаем вид, что мы этого не понимаем. Вместо этого придем к тому же выводу, используя метод рецессии. Если Х = 1, то Ý = (β1+ β2) в соответствии с уравнением регрессии. Если X=2, то Ý = (β1+ 2β2). Следовательно, мы можем сформировать табл. 1.1. Таким образом, остаток для первого наблюдения (е1), который задается выражением (Y1 - Ý 1), равен (3 - β1 - β2), и е2, заданный выражением (Y2- Ý 2), равен (5 - β1 -β2). Следовательно, RSS = (3 – b1 – b2)2 + (5 – b1 – 2b2)2 = 9 + b12 + b22 - 6b1 – 6b2 + 2b1b2 + 25 + b12 + 4b22 – 10b1 – 20b2 + 4b1b2 = 34 + 2b12 + 5b22 – 16b1 – 26b2 + 6b1b2 (1.8)
Теперь мы хотим выбрать такие значения b1 и b2 чтобы значение RSS было минимальным. Для этого мы используем дифференциальное исчисление и находим значения b1 и b2 удовлетворяющие следующим соотношениям:
Взяв частные производные, получаем
и
Таким образом, мы имеем
и
Решив эти два уравнения, получим b1 = 1 и b2 = 2, следовательно, уравнение регрессии будет иметь следующий вид:
Для того чтобы проверить, что мы пришли к правильному выводу, вычислим остатки:
Таким образом, оба остатка равны нулю, что означает, что линия проходит точно через обе точки. И это мы, разумеется, знали с самого начала. Пример 2 Используем пример, рассмотренный в предыдущем разделе, и добавим третье наблюдение: Y равен 6 при X = 3. Три наблюдения, показанные на рис.1.5, не лежат на одной прямой, поэтому точное соответствие получить
невозможно. В этом случае для вычисления положения прямой мы используем регрессию по методу наименьших квадратов. Начнем с задания стандартного уравнения
Для значений X, равных 1, 2 и 3, расчетные значения Y равны соответственно (
Следовательно,
Условия первого
Решая систему этих двух уравнений, получим b1 = 1,67 и b2 = 1,50. Следовательно, уравнение регрессии имеет следующий вид:
Три наблюдения и линия регрессии представлены на рис. 1.6.
Вывод следствии гипотезы Если гипотеза H0 верна, то значения b2, полученные в ходе регрессионного анализа, будут иметь распределение с математическим ожиданием Персией имеет нормальное распределение. Если это так, то величина b2 будет также нормально распределена, как показано на рис. 2.6. Сокращение «sd» на рисунке соответствует величине стандартного отклонения оценки b2 т.е.
Сначала мы допустим, что знаем величину стандартного отклонения величины b2. Это наиболее нереалистичное допущение, и мы позднее отбросим его. На практике же значение этого отклонения (так же, как и неизвестные значения параметров (β1 и β2) подлежит оценке. Можно, тем не менее, упростить обсуждение, предположив, что точное значение отклонения известно, и, следовательно, у нас есть возможность построить график, показанный на рис. 2.6. Проиллюстрируем это на примере модели связи общей инфляции и инфляции, вызванной ростом заработной платы (2.61). Предположим, что некоторым образом мы знаем, что стандартное отклонение величины b2 составляет 0,1. Тогда, если нулевая гипотеза H0: β 2 = 1 верна, то оценки коэффициентов регрессии будут распределены так, как это показано на рис. 2.7. Из этого рисунка можно видеть, что при справедливости нулевой гипотезы оценки будут находиться приблизительно между 0,8 и 1,2. Примеры В разделе 1.6 была оценена регрессия величины заработка на число лет обучения по данным Всеамериканского опроса молодежи, распечатка для которой приведена в табл. 2.6. В первых двух ее столбцах указаны названия переменных, здесь это S и свободный член (Stata обозначает его как _cons), и оценки их коэффициентов. В третьем столбце приведены соответствующие стандартные ошибки. Предположим, что одна из задач оценивания регрессии состояла в подтверждении нашей догадки о том, что размер заработка зависит от продолжительности полученного образования. Соответственно, мы формируем нулевую гипотезу Н0: β2 = 0, и затем пытаемся опровергнуть ее. Соответствующая t-cтатистика, вычисленная по формуле (2.71), есть оценка коэффициента, деленная на ее стандартную ошибку:
Так как в выборку включено 540 наблюдений, и мы оценили два параметра, то число степеней свободы составляет 538. В табл. А.2 отсутствуют критические значения t для 538 степеней свободы, но мы знаем, что они должны быть меньше, чем соответствующие критические значения для 500 степеней свободы, так как критическое значение есть убывающая функция числа степеней свободы. Критическое значение для 500 степеней свободы при 5%-ном уровне значимости равняется 1,965. Следовательно, мы можем с уверенностью отвергнуть H0, сделав вывод о том, что продолжительность обучения влияет на размер заработка. Если этот критерий описать словами, то верхний и нижний 1.5%-ные «хвосты» t-распределения при 538 степенях свободы начинаются со стандартных отклонений (1,965 вверх и вниз) от его математического ожидания, равного нулю. Коэффициент регрессии, который по оценкам находится в пределах 1,965 стандартного отклонения от гипотетического значения, не приводит к отказу от последнего. В рассматриваемом случае расхождение будет эквивалентно 10,59 стандартного отклонения, и мы приходим к выводу о том, что результат регрессии противоречит нулевой гипотезе. Конечно, поскольку мы используем уровень значимости 5% в качестве основы для проверки гипотезы, существует 5%-ный риск допустить ошибку I рода. В этом случае мы могли бы снизить риск до 1% за счет применения уровня значимости в 1 %. Критическое значение для / при 1 % -ном уровне зна-чимости с 500 степенями свободы составляет 2,586. Поскольку /-статистика превышает это число, мы видим, что можно легко отказаться от нулевой гипотезы также и на этом уровне значимости.
Таблица 2.6
Отметим, что если 5%- и 1 %-ный тесты приводят к одному и тому же выводу, то нет необходимости представлять результаты обоих, и если это сделать, то это может быть расценено как некомпетентность. По этому вопросу прочтите внимательно Вставку 2.5 о представлении результатов оценивания регрессии. Процедура установления взаимосвязи между зависимой и объясняющей переменными путем высказывания, а затем отклонения нулевой гипотезы H0: β2 = 0, используется очень часто. Соответственно все серьезные регрессионные программы автоматически выводят t-статистику для этого специального случая; иными словами, коэффициент делится на его стандартную ошибку. Данное отношение часто обозначается как «t-статистика». В приведенной распечатке результатов значения t-статистики для постоянного члена и коэффициента наклона показаны в среднем столбце. Если, однако, нулевая гипотеза определяет некоторое ненулевое значение величины β2, то необходимо использовать более общее выражение (2.71), Значения р Пятый столбец результатов расчетов в табл. 2.6, озаглавленный Р >\t\, представляет альтернативный подход к описанию значимости коэффициентов регрессии. Числа в этом столбце показывают значения р для каждого коэффициента. Это вероятности получения соответствующих значений t-статистку если нулевая гипотеза Н0: (β2 = 0 верна. Значение p меньшее, чем 0,01, означает, что эта вероятность меньше, чем 1%, что, в свою очередь, означает, чтонулевая гипотеза была бы отклонена при 1%-ном уровне значимости; значение p между 0,01 и 0,05 означает, что нулевая гипотеза была бы отклонена при5%-ном уровне значимости, но не при 1%-ном. Величина p, равная или превышающая 0,05, свидетельствует, что нулевая гипотеза не была бы отклонена при 5%-ном уровне значимости. Подход, основанный на значениях p более информативен, чем подход, основанный на задании с 5%- и 1%-ного уровня значимости, поскольку он дает точную вероятность ошибки I рода, если нулевая гипотеза верна. Например, в табл. 2.6 для функции заработка, приведенной выше, значение р для коэффициента наклона равно 0,0000, что означает, что вероятность получения t-статистики 10,59 или больше составляет здесь менее чем 0,005%. Следовательно мы отвергнем гипотезу о равенстве нулю коэффициента наклона при 1%-н: уровне значимости. В действительности мы отвергли бы здесь ее и при yровне значимости 0,1% (см. следующий подраздел). Выбор между подходом, основанным на значении р, и подходом с заданием уровня значимости 5%(1%) может быть основан на негласном соглашении. Так, в медицинской литературе используются значения p, в то время как в экономической литературе обычно применяются оценки 5%- и 1%-ного уровня значимости. Доверительные интервалы До сих пор мы предполагали, что гипотеза предшествует эмпирическим исследованиям. Однако это необязательно. Очень часто теория и эксперимент взаимодействуют, в этом отношении типичным примером является регрессия для функции заработка. Вначале мы оцениваем регрессию, потому что в соответствии с экономической теорией ожидаем, что продолжительность полученного образования влияет на заработок. Результат оценивания регрессии подтвердил это интуитивное ожидание в том смысле, что мы отвергли нулевую гипотезу β 2 = 0, но после этого возникло ощущение некоторой пустоты поскольку наша теория неспособна выдвинуть предположение о том, что значение (β 2 равняется некоторому конкретному числу. Теперь, однако, мы можем двинуться в противоположном направлении и задаться вопросом о том, какие гипотезы совместимы с результатом оценивания нашей регрессии.
Вполне очевидно, что гипотеза о том, что β 2 = 2,455, будет совместимой, так как гипотеза и результаты эксперимента совпадают. Кроме того, совместимыми будут и гипотезы о том, что β 2 = 2,454 и β2 = 2,456, так как разница между гипотезой и результатом эксперимента будет небольшой. Вопрос состоит в том, насколько сильно гипотетическое значение может отличаться от результата эксперимента, прежде чем они станут несовместимыми и мы должны будем отклонить нулевую гипотезу. Мы можем ответить на этот вопрос, используя предшествующие рассуждения. Из уравнения (2.72) мы можем видеть, что коэффициент регрессии b2 и гипотетическое значение β2 будут несовместимыми, если выполняются условия
т.е. если
что соответствует
Отсюда следует, что гипотетическое значение β2 является совместимым с результатом оценивания регрессии, если одновременно выполнены условия
т.е. если величина β2 удовлетворяет двойному неравенству
Любое гипотетическое значение для β2, которое удовлетворяет соотношению (2.80), будет автоматически совместимо с оценкой b 2, иными словами, не будет опровергаться ею. Множество всех этих значений, определенных как интервал между нижней и верхней границами неравенства, известно как доверительный интервал для величины β2. Отметим, что границы доверительного интервала одинаково отстоят от b 2. Отметим также, что так как значение tкрит зависит от выбора уровня значимости, границы будут также зависеть от этого выбора. Если принимается 5%-ный уровень значимости, то соответствующий доверительный интервал известен как 95%-ный интервал. Если выбирается 1%-ный уровень, то можно получить доверительный интервал с 99% и т.д. Так как t крит будет больше для 1%-ного уровня, чем для 5%-ного (при любом данном числе степеней свободы), то, следовательно, интервал в 99% будет шире интервала в 95%. Он включает все гипотетические значения для β2 в 95%-ном доверительном интервале, а также дополнительные промежутки с той и с другой стороны.
Вставка 2.7. Вторая интерпретаций доверительного интервала Когда вы строите доверительный интервал, числа, которые вы определяете в качестве его верхнего и нижнего пределов, содержат случайные составляющие, которые зависят от значений случайного члена в наблюдениях выборки. Например, неравенство (2.80) включает верхний предел
Как b2, так и с.о.(b2) частично определяются значениями случайного члена. Мы надеемся, что доверительный интервал будет включать истинное значение параметра, но иногда он будет так искажен случайными факторами, что это будет не так. Какова же вероятность того, что доверительный интервал будет включать истинное значение параметра? Легко показать, используя элементарную теорию вероятности, что в случае 95%-ного доверительного интервала данная вероятность составляет 95% при условии, что модель правильно определена и что предпосылки, перечисленные в разделе 2.2 выполнены. Аналогичным образом, в случае 99%-ного доверительного интервала данная вероятность составляет 99%. Оцененный коэффициент (например, b2 в неравенстве (2.80)) обеспечивает точечную оценку рассматриваемого параметра, но при этом вероятность того, что истинное значение будет в точности равно этой оценке, ничтожно мала. Доверительный интервал дает так называемую «интервальную оценку» параметра, т.е. диапазон значений, который будет включать истинное значение с высокой > заранее определенной вероятностью. Именно эта интерпретация и дает название доверительному интервалу. (Более подробно этот вопрос рассматривается в работе Т. Уоннакотга и Р. Уоннакотта (Wannacott, Wannacott, 1990), гл. 8.)
Пример В распечатке для функции заработка, представленной в табл. 2.6, коэффициент при переменной S составил 2,455, его стандартная ошибка равнялась 0,232, а критическое значение t при 5%-ном уровне значимости — примерно 1,965. Отсюда соответствующий 95%-ный доверительный интервал составляет
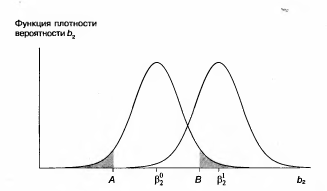
Иными словами, 1,999 < Поэтому мы отвергаем гипотетические значения только свыше 1,999 и ниже 2,911. Любые гипотетические значения внутри этих пределов не будут опровергаться полученным результатом регрессии. Доверительный интервал показан в последнем столбце распечатки программы Stata. Это, однако, не является стандартным свойством регрессионных пакетов, и обычно приходится рассчитывать интервал самостоятельно. Односторонние t-критерии В нашем обсуждении t-критериев мы начали с нулевой гипотезы Н0: H0: В этом случае по каким-то причинам существуют только два возможных истинных значения коэффициента при X, равных Предположим, что мы хотим проверить гипотезу Н0 при 5%-ном уровне значимости и используем для этого обычную процедуру, которая уже рассматривалась в этой главе. Мы находим границы для верхнего и нижнего 2,5%-ных «хвостов» t-распределения, считая, что Н0 верна, обозначив их как А и В на рис. 2.10, и гипотеза H0 отклоняется, если коэффициент регрессии b2 оказывается левее точки А или правее точки В. Далее, если значение b2 находится справа от 5, то оно намного лучше совместимо с гипотезой H1 чем с гипотезой H0; вероятность его нахождения справа от В, если истинна H1 намного больше, чем при истинности гипотезы H0. Здесь у нас не должно быть сомнений в том, чтобы отклонить гипотезу Н0. Следовательно, мы делаем вывод, что гипотеза H1 верна. Если, однако, b2 находится слева от А, то используемая процедура проверки приведет нас к неверному заключению. Последняя требует отклонить гипотезу H0 и, следовательно, принять гипотезу H1 несмотря на то, что при истинности гипотезы Н1 вероятность нахождения b2 слева от А ничтожно мала. Мы даже не построили график функции плотности вероятности, соответствующей гипотезе Н1. Если такое значение b2 получается только раз на миллион случаев при истинности H1 но в 2,5% случаев при истинности H0, то здесь намного логичнее считать, что истинной является гипотеза Н0. Конечно, в од-
Рисунок 2.10. Распределение величины b2 в соответствии с гипотезами Н0 и Н 1 ном случае на миллион вы сделаете ошибку, но в остальных случаях вы будете правы. Следовательно, мы будем отклонять H0, только если b2 оказывается на верхнем 2,5%-ном «хвосте» распределения, т.е. справа от В. Это означает, что теперь мы выполняем проверку гипотезы с односторонним критерием, сократив в результате вероятность допустить ошибку I рода до 2,5%. Поскольку уровень значимости определен как вероятность допустить ошибку I рода, то он теперь также составляет 2,5%. Как уже отмечалось, экономисты обычно предпочитают проверку гипотез с 5%- и 1%-ным уровнями значимости проверкам с 2,5%-ным уровнем значимости. Если вы хотите провести проверку с 5%-ным уровнем значимости, то вы должны переместить точку В влево так, чтобы получить 5% вероятности в «хвосте» распределения и увеличить вероятность допустить ошибку I рода до 5%. (Вопрос: Почему намеренно выбирается увеличение вероятности допустить ошибку I рода? Ответ: потому что одновременно сокращается вероятность допустить ошибку II рода, т.е. вероятность того, что нулевая гипотеза не будет отклонена, когда она является ложной. В большинстве случаев нулевая гипотеза состоит в том, что соответствующий коэффициент равен нулю, и вы пытаетесь опровергнуть это, показав, что рассматриваемая переменная действительно имеет влияние. В такой ситуации при выборе одностороннего критерия вы уменьшаете риск не отвергнуть ложную нулевую гипотезу, в то время как вероятность ошибки I рода сохраняется на 5%-ном уровне.) Если стандартное отклонение величины b2 известно (что практически маловероятно), а распределение нормально, то точка В будет находиться в z стандартных отклонениях вправо от Аналогично, если вы хотите выполнить проверку с уровнем значимости 1%, то вы перемещаете В вправо до той точки, где «хвост» распределения со-
держит 1% вероятности. Если вам пришлось вычислить стандартную ошибку величины b2 на основе выборочных данных, то нужно найти критическое значение для t вколонке, соответствующей 1%. В проведенном обсуждении мы допустили, что Мощность критерия В данном конкретном случае мы можем вычислить вероятность допустить ошибку II рода, т.е. принять ложную гипотезу. Предположим, что мы приняли ложную гипотезу H0: Используя односторонний критерий вместо двустороннего, можно получить большую мощность для любого уровня значимости. Как мы уже видели, при переходе к одностороннему критерию с 5%-ным уровнем значимости точка В на рисунке сдвигается влево и, тем самым, снижается вероятность принятия гипотезы H0, если она ложна. H0:
Мы рассмотрели случай, когда альтернативная гипотеза включала конкретное гипотетическое з
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.19.205 (0.015 с.) |



 и
и  (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11)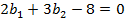 (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14) (1.15)
(1.15) (1.16)
(1.16)
 (1.17)
(1.17) ), (
), ( ) и (bl+3b2), они приведены в табл. 1.2.
) и (bl+3b2), они приведены в табл. 1.2.
 (1.18)
(1.18) (1.19)
(1.19) (1.20)
(1.20) (1.21)
(1.21)
 и дис-
и дис- . Теперь мы вводим допущение, что случайный член и
. Теперь мы вводим допущение, что случайный член и . Учитывая структуру нормального распределения, большинство оценок параметра b2 будет находиться в пределах двух стандартных отклонений от
. Учитывая структуру нормального распределения, большинство оценок параметра b2 будет находиться в пределах двух стандартных отклонений от  (2.73)
(2.73)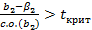 или
или 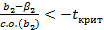 (2.76)
(2.76)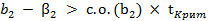 или
или 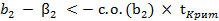 (2.77)
(2.77)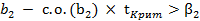 или
или 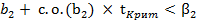 (2.78)
(2.78) и
и 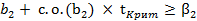 (2.79)
(2.79) (2.80)
(2.80)
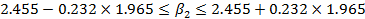 (2.81)
(2.81)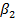 < 2,911. (2.82)
< 2,911. (2.82)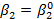 и провели проверку возможности ее отклонения при коэффициенте регрессии, равном b2. Если бы мы отклонили эту гипотезу, то косвенно приняли бы альтернативную гипотезу Н1:
и провели проверку возможности ее отклонения при коэффициенте регрессии, равном b2. Если бы мы отклонили эту гипотезу, то косвенно приняли бы альтернативную гипотезу Н1:  . До сих пор альтернативная гипотеза была лишь простым отрицанием нулевой гипотезы. Если, однако, мы можем сформулировать альтернативную гипотезу более конкретно, то мы должны и усовершенствовать процедуру проверки. Проведем исследование трех случаев: первый случай — весьма частный, когда существует единственное альтернативное истинное значение
. До сих пор альтернативная гипотеза была лишь простым отрицанием нулевой гипотезы. Если, однако, мы можем сформулировать альтернативную гипотезу более конкретно, то мы должны и усовершенствовать процедуру проверки. Проведем исследование трех случаев: первый случай — весьма частный, когда существует единственное альтернативное истинное значение 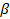 2, которое мы обозначим
2, которое мы обозначим 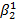 ; второй случай — если
; второй случай — если  .
.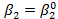 , H1:
, H1: 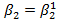
 , H1:
, H1: 



