
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулирование нулевой гипотезыСодержание книги
Поиск на нашем сайте
Начнем с допущения о том, что теория предшествует эксперименту и что вы уже имеете в виду некоторую гипотетическую связь или зависимость. Например, вы можете считать, что темп общей инфляции в экономике (p, в %) зависит от темпа инфляции, вызванной ростом заработной платы (w, в %), и что эта зависимость описывается линейным уравнением:
где p1 и р2 — параметры, а u — случайный член. Далее вы можете построить гипотезу о том, что без учета эффектов, вносимых случайным членом, общая инфляция увеличивается в той же степени, что и инфляция, вызванная ростом заработной платы. В этих условиях вы можете сказать, что гипотеза, которую вы собираетесь проверять, известная как ваша нулевая гипотеза и обозначенная H0, состоит в том, что β2 равняется единице. Мы также определяем альтернативную гипотезу, обозначаемую Н1, которая представляет заключение. которое делается в том случае, если экспериментальная проверка указала на ложность H0. В данном случае эта гипотеза состоит в том, что H0:β2=1; H1:β2≠1. В этом конкретном случае, если мы действительно считаем, что общая инфляция равна инфляции, вызванной ростом заработной платы, мы делаем попытку защитить нулевую гипотезу H0, подвергнув ее максимально строгой проверке и надеясь, что она не будет опровергнута. Однако на практике более обычным является построение нулевой гипотезы, которая затем будет проверяться с помощью альтернативной гипотезы, которая предполагается верной Например, рассмотрим простую функцию заработка:
где EARNINGS — часовой заработок в долларах, a S — число законченных лет обучения. Исходя из вполне разумных теоретических оснований, вы предполагаете, что заработок зависит от продолжительности обучения, но ваша теория недостаточно «сильна», чтобы можно было определить конкретное значение для β2. Тем не менее, вы можете установить наличие зависимости величины заработка от S, используя для этого обратную процедуру, когда в качестве нулевой гипотезы принимается утверждение о том, что величина заработка не зависит от S, т.е. что β2 равняется нулю. Альтернативная гипотеза заключается в том, что величина β2 не равняется нулю, иными словами, что величина S влияет на размер заработка. Если вы можете отвергнуть нулевую гипотезу, то вы таким образом устанавливаете наличие зависимости, по крайней мере вобщих чертах. С использованием введенной системы обозначений, ваши нулевая и альтернативная гипотезы примут вид H0: β2 = 0 и Н1: β2 ≠ 0 соответственно. Последующий анализ касается модели парной регрессии
Он будет относиться только к коэффициенту наклона β2, но точно такие ж с процедуры применимы и к постоянному члену β1 Возьмем общий случай, вкотором в нулевой гипотезе утверждается, что β2 равно некоторому конкретному значению, например Вывод следствии гипотезы Если гипотеза H0 верна, то значения b2, полученные в ходе регрессионного анализа, будут иметь распределение с математическим ожиданием Персией имеет нормальное распределение. Если это так, то величина b2 будет также нормально распределена, как показано на рис. 2.6. Сокращение «sd» на рисунке соответствует величине стандартного отклонения оценки b2 т.е.
Сначала мы допустим, что знаем величину стандартного отклонения величины b2. Это наиболее нереалистичное допущение, и мы позднее отбросим его. На практике же значение этого отклонения (так же, как и неизвестные значения параметров (β1 и β2) подлежит оценке. Можно, тем не менее, упростить обсуждение, предположив, что точное значение отклонения известно, и, следовательно, у нас есть возможность построить график, показанный на рис. 2.6. Проиллюстрируем это на примере модели связи общей инфляции и инфляции, вызванной ростом заработной платы (2.61). Предположим, что некоторым образом мы знаем, что стандартное отклонение величины b2 составляет 0,1. Тогда, если нулевая гипотеза H0: β 2 = 1 верна, то оценки коэффициентов регрессии будут распределены так, как это показано на рис. 2.7. Из этого рисунка можно видеть, что при справедливости нулевой гипотезы оценки будут находиться приблизительно между 0,8 и 1,2.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.55.138 (0.006 с.) |

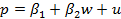 (2.61)
(2.61)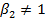 . Две гипотезы сформулированы с использованием следующих обозначений:
. Две гипотезы сформулированы с использованием следующих обозначений: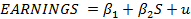 (2.62)
(2.62)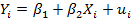 (2.65)
(2.65) , и альтернативная гипотеза состоит в том, что β2 не равно этому значению (H0: β2 =
, и альтернативная гипотеза состоит в том, что β2 не равно этому значению (H0: β2 =  . Теперь мы вводим допущение, что случайный член и
. Теперь мы вводим допущение, что случайный член и . Учитывая структуру нормального распределения, большинство оценок параметра b2 будет находиться в пределах двух стандартных отклонений от
. Учитывая структуру нормального распределения, большинство оценок параметра b2 будет находиться в пределах двух стандартных отклонений от 


