
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сопоставимость, случайность и уровень значимостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теперь приступим к главному. Предположим, что мы взяли фактическую выборку из наблюдений общей инфляции и инфляции, вызванной ростом заработной платы, и построили оценку β2, используя для этого регрессионный анализ. Если оценка близка к единице, то мы должны быть полностью удовлетворены нулевой гипотезой, так как она и результат оценивания для выборки совместимы друг с другом. Предположим, с другой стороны, что оценка значительно отличается от единицы. Допустим, например, что она равна 0,7. Это составит три стандартных отклонения вниз от 1,0. Если нулевая гипотеза верна, то вероятность того, что отличие b2 от среднего достигнет трех стандартных отклонений в положительную или отрицательную сторону, составляет лишь 0,0027, т.е. очень низка.
Рисунок 2.6. Структура нормального распределения оценки b2 в единицах стандартных отклонений от математического ожидания
Рисунок 2.7. Пример распределения величины b2 (модель связи общей инфляции и инфляции, вызванной ростом заработной платы)
Исходя из этого вызывающего беспокойство результата, вы можете прийти к одному из двух выводов: 1. Вы можете продолжать считать, что ваша нулевая гипотеза H0: (β2 = 1 верна и что эксперимент дал случайный результат. Вы допускаете, что вероятность получения такого низкого значения для b2 является очень небольшой. но, тем не менее, она имеет место в 0,27% случаев, и вы допускаете, что это именно тот случай. 2. Вы можете сделать вывод о том, что гипотеза противоречит результат) оценивания регрессии. Вы не удовлетворяетесь объяснением, данным в пункте 1, так как вероятность очень мала, и понимаете, что наиболее правдоподобным объяснением является то, что величина β2 вовсе не равняется единице. Другими словами, вы принимаете альтернативную гипотезу H1: β2≠ 1. Каким образом вы определите, когда необходимо выбрать первый вывод, а когда — второй? Очевидно, что чем меньше вероятность получения регрессии, подобной той, которую вы получили при условии правильности вашей гипотезы, тем больше вероятность вашего отказа от гипотезы и тем очевиднее переход ко второму выводу. Насколько малой должна быть указанная вероятность для выбора второго вывода? На этот вопрос нет и не может быть определенного ответа. В большинстве работ по экономике за критический уровень берется 5 или 1%. Если выбирается уровень 5%, то переключение на второй вывод происходит в том случае. когда при истинности нулевой гипотезы вероятность получения столь экстремального значения для b2 составляет менее 5%. В этом случае говорят, что нулевая гипотеза должна быть отвергнута при 5%-ном уровне значимости. Это происходит в том случае, когда величина b2 отстоит от величины z> 1,96 или z< -1,96, (2.64) где z — число стандартных отклонений между регрессионной оценкой и гипотетическим значением для β2:
Нулевая гипотеза не будет отвергнута, если -1,96 <z< 1,96. (2.66) Это условие можно записать с помощью величин b2 и -1,96 ≤ Умножив все части неравенства на стандартное отклонение величины b2 можно получить -1,96 s.d.(b 2) ≤ b2 - а из этого соотношения можно получить следующее:
Уравнение (2.69) дает множество значений для величины b2, которые не приводят к отказу от конкретной нулевой гипотезы о том, что β2 =
Рисунок 2.8. Область принятия гипотезы для величины Ь2 при 5%-ном уровне значимости Аналогичным образом считается, что нулевая гипотеза должна быть отвергнута при уровне значимости в 1%, если гипотеза подразумевает, что вероятность получения столь экстремального значения для величины b2 составляет менее 1%. Это происходит тогда, когда величина b2 отстоит на более чем 2.58стандартного отклонения вверх или вниз от гипотетического значения величины β2, т.е. когда z > 2,58 или z< -2,58. (2.70) Вставка 2.4. Ошибки I и II рода в повседневной жизни Проблема избежать допущения ошибок I и II рода известна всем. Типичным примером этого является расследование уголовного преступления. Если за нулевую гипотезу принять то, что подсудимый невиновен, то ошибка I рода происходит тогда, когда суд присяжных признает его виновным. Ошибка II рода имеет место в том случае, когда суд присяжных ошибочно оправдывает виновного подсудимого. Опять возвратившись к таблице нормального распределения, вы может видеть, что вероятность того, что величина b2 будет более чем на 2,58 стандартного отклонения отстоять вверх от своего математического ожидания, составляет 0,5%, и та же самая вероятность для нахождения этой величины ниже своего математического ожидания более чем на 2,58 стандартного отклонения. Таким образом, общая вероятность получения столь экстремальных значений составляет 1 %. В нашем примере вы отвергнете нулевую гипотезу о том что β2 = 1, если оценка коэффициента регрессии будет находиться выше 1.258 или ниже 0,742. Можно задаться вопросом, почему исследователи обычно представляют результаты при уровнях значимости 5 и 1%. Почему недостаточно ограничиться только одним уровнем? Причина заключается в том, что обычно делается попытка найти баланс между риском допущения ошибок I и II рода. Ошибка I рода имеет место в том случае, когда вы отвергаете истинную нулевую гипотезу. Ошибка II рода возникает тогда, когда вы не отвергаете ложную гипотезу. Очевидно, что чем ниже критическая вероятность, тем меньше риск получения ошибок I рода. Если вы используете уровень значимости, равный 5%, то вы будете отвергать истинную гипотезу в 5% случаев. Если уровень значимости составляет 1%, то вы будете делать ошибку I рода в 1% случаев. Таким образом, в этом отношении 1%-ный уровень значимости более надежен. Если вы отвергли гипотезу на этом уровне, вы почти наверняка были вправе сделать это. Именно по этой причине 1%-ный уровень значимости описывается как «более высокий» в сравнении с 5%-ным уровнем. В то же время, если нулевая гипотеза ложна, то чем выше ваш уровень значимости, тем шире ваша область принятия гипотезы, тем выше вероятность того, что вы не отвергнете ее, и тем выше риск допущения ошибки II рода. Таким образом, вы оказываетесь перед дилеммой. Если вы будете настаивать на очень высоком уровне значимости, то столкнетесь с относительно высоким риском допущения ошибки II рода, если гипотеза окажется ложной. Если вы выбираете низкий уровень значимости, то оказываетесь перед относительно высоким риском допущения ошибки I рода, если гипотеза истинна. Большинство людей выбирают достаточно простую форму обеспечения гарантий и осуществляют проверку на обоих уровнях значимости, представляя результаты каждой такой проверки. На самом деле часто нет никакой необходимости непосредственно ссылаться на оба результата. Так как величина b2 должна быть более «экстремальной» для гипотезы, отвергаемой при 1 %-ном уровне значимости, чем при 5%-ном, и если вы отклоняете ее при 1 %-ном уровне, то из этого автоматически следует, что вы отклоните ее и при уровне значимости в 5%, и нет необходимости упоминать об этом. Если же вы не отвергаете гипотезу при уровне значимости в 5%, то из этого автоматически следует, что вы не отвергнете ее и при 1 %-ном уровне значимости. Только в одном случае вы должны представить оба результата: если гипотеза отвергается на 5%-ном, но не на 1%-ном уровне значимости. t -ТЕСТЫ До сих пор мы считали, что стандартное отклонение величины b2 известно. Однако на практике это допущение нереально. Это можно показать на примере стандартной ошибки для величины b2 взятой из уравнения (2.44). Это приводит к двум изменениям процедуры проверки гипотез. Во-первых, величина z определяется на основе использования стандартной ошибки с.о.(b 2) вместо стандартного отклонения s.d.(b 2) и носит название t-статистики:
Во-вторых, критические уровни t определяются величиной, имеющей так называемое t -распределение вместо нормального распределения. Мы не будем вдаваться в причины этого или даже описывать t -распределение математически. Достаточно будет сказать, что оно родственно нормальному распределению, а его точная форма зависит от числа степеней свободы в регрессии, и оно все лучше аппроксимируется нормальным распределением по мере увеличения числа степеней свободы. Вы, конечно, уже встречали понятие t- распределения во вводном курсе статистики. В табл. А.2 Приложения А представлены критические значения для t, сгруппированных по уровням значимости и числу степеней свободы. Оценивание каждого параметра в уравнении регрессии поглощает одну степень свободы в выборке. Отсюда число степеней свободы равняется числу наблюдений в выборке минус число оцениваемых параметров. Параметрами являются постоянный член (при условии, что он введен в модель регрессии) и коэффициенты при независимых переменных. В рассматриваемом случае парной регрессии оцениваются только два параметра β1 и β2, поэтому число степеней свободы составляет (п - 2). Следует подчеркнуть, что когда мы перейдем к множественному регрессионному анализу, потребуется более общее выражение. Критическое значение для t, которое мы обозначим как tкрит, заменит число 1,96 в уравнении (2.67). Задача t-теста состоит в том, чтобы сравнить t-статистику и t крит. Таким образом, условие того, что оценка регрессии не должна приводить к отказу от нулевой гипотезы HQ: β2 =
Следовательно, мы имеем правило для принятия решения: H0 отвергается, если
Примеры В разделе 1.6 была оценена регрессия величины заработка на число лет обучения по данным Всеамериканского опроса молодежи, распечатка для которой приведена в табл. 2.6. В первых двух ее столбцах указаны названия переменных, здесь это S и свободный член (Stata обозначает его как _cons), и оценки их коэффициентов. В третьем столбце приведены соответствующие стандартные ошибки. Предположим, что одна из задач оценивания регрессии состояла в подтверждении нашей догадки о том, что размер заработка зависит от продолжительности полученного образования. Соответственно, мы формируем нулевую гипотезу Н0: β2 = 0, и затем пытаемся опровергнуть ее. Соответствующая t-cтатистика, вычисленная по формуле (2.71), есть оценка коэффициента, деленная на ее стандартную ошибку:
Так как в выборку включено 540 наблюдений, и мы оценили два параметра, то число степеней свободы составляет 538. В табл. А.2 отсутствуют критические значения t для 538 степеней свободы, но мы знаем, что они должны быть меньше, чем соответствующие критические значения для 500 степеней свободы, так как критическое значение есть убывающая функция числа степеней свободы. Критическое значение для 500 степеней свободы при 5%-ном уровне значимости равняется 1,965. Следовательно, мы можем с уверенностью отвергнуть H0, сделав вывод о том, что продолжительность обучения влияет на размер заработка. Если этот критерий описать словами, то верхний и нижний 1.5%-ные «хвосты» t-распределения при 538 степенях свободы начинаются со стандартных отклонений (1,965 вверх и вниз) от его математического ожидания, равного нулю. Коэффициент регрессии, который по оценкам находится в пределах 1,965 стандартного отклонения от гипотетического значения, не приводит к отказу от последнего. В рассматриваемом случае расхождение будет эквивалентно 10,59 стандартного отклонения, и мы приходим к выводу о том, что результат регрессии противоречит нулевой гипотезе. Конечно, поскольку мы используем уровень значимости 5% в качестве основы для проверки гипотезы, существует 5%-ный риск допустить ошибку I рода. В этом случае мы могли бы снизить риск до 1% за счет применения уровня значимости в 1 %. Критическое значение для / при 1 % -ном уровне зна-чимости с 500 степенями свободы составляет 2,586. Поскольку /-статистика превышает это число, мы видим, что можно легко отказаться от нулевой гипотезы также и на этом уровне значимости.
Таблица 2.6
Отметим, что если 5%- и 1 %-ный тесты приводят к одному и тому же выводу, то нет необходимости представлять результаты обоих, и если это сделать, то это может быть расценено как некомпетентность. По этому вопросу прочтите внимательно Вставку 2.5 о представлении результатов оценивания регрессии. Процедура установления взаимосвязи между зависимой и объясняющей переменными путем высказывания, а затем отклонения нулевой гипотезы H0: β2 = 0, используется очень часто. Соответственно все серьезные регрессионные программы автоматически выводят t-статистику для этого специального случая; иными словами, коэффициент делится на его стандартную ошибку. Данное отношение часто обозначается как «t-статистика». В приведенной распечатке результатов значения t-статистики для постоянного члена и коэффициента наклона показаны в среднем столбце. Если, однако, нулевая гипотеза определяет некоторое ненулевое значение величины β2, то необходимо использовать более общее выражение (2.71),
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.008 с.) |



 более чем на 1,96 стандартного отклонения. Если вы посмотрите на таблицу нормального распределения (табл. А.1 в Приложении А), то вы увидите, что вероятность того, что величина b2 будет превосходить среднее значение на более чем 1,96 стандартного отклонения, составляет 2,5%, и, аналогичным образом, вероятность того, что эта величина будет более чем на 1,96 стандартного отклонения ниже среднего значения, также составляет 2,5%. Общая вероятность того, что данная величина отстоит от математического ожидания более чем на 1,96 стандартного отклонения, составляет, таким образом, 5%. Мы можем обобщить это решающее правило в математической форме, полагая, что нулевая гипотеза отвергается, если:
более чем на 1,96 стандартного отклонения. Если вы посмотрите на таблицу нормального распределения (табл. А.1 в Приложении А), то вы увидите, что вероятность того, что величина b2 будет превосходить среднее значение на более чем 1,96 стандартного отклонения, составляет 2,5%, и, аналогичным образом, вероятность того, что эта величина будет более чем на 1,96 стандартного отклонения ниже среднего значения, также составляет 2,5%. Общая вероятность того, что данная величина отстоит от математического ожидания более чем на 1,96 стандартного отклонения, составляет, таким образом, 5%. Мы можем обобщить это решающее правило в математической форме, полагая, что нулевая гипотеза отвергается, если: (2,65)
(2,65) ≤ 1,96. (2.67)
≤ 1,96. (2.67) . Это множество значений получило название области принятия гипотезы для b2 при 5%-ном уровне значимости. В нашем примере модели связи общей инфляции и инфляции, вызванной ростом заработной платы, где s.d.(b2) равняется 0,1, можно отвергнуть гипотезу при уровне значимости в 5%, если величина b2 находится выше или ниже гипотетического среднего значения на величину более 0,196, т.е. выше 1,196 или ниже 0,804. Таким образом, область принятия гипотезы включает значения величины b2 от 0,804 до 1,196. Это показано не-затененной областью на рис. 2.8
. Это множество значений получило название области принятия гипотезы для b2 при 5%-ном уровне значимости. В нашем примере модели связи общей инфляции и инфляции, вызванной ростом заработной платы, где s.d.(b2) равняется 0,1, можно отвергнуть гипотезу при уровне значимости в 5%, если величина b2 находится выше или ниже гипотетического среднего значения на величину более 0,196, т.е. выше 1,196 или ниже 0,804. Таким образом, область принятия гипотезы включает значения величины b2 от 0,804 до 1,196. Это показано не-затененной областью на рис. 2.8
 (2.71)
(2.71)
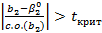 , и она не отвергается, если
, и она не отвергается, если  , где
, где  - абсолютная величина (модуль) значения t.
- абсолютная величина (модуль) значения t. (2.73)
(2.73)


