
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация уровней статистической значимости (р-уровней)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В данной классификации уровней значимости имеется произвол и это является всего лишь неформальным соглашением, принятым на основе практического опыта. Имея серию экспериментов (множество анализов), мы всегда можем выбирать те результаты, которые подтверждают нашу гипотезу. Многие методы исследований (особенно простые) не используют специальную корректировку, или поправку, на общее число сравнений и многие способы не предполагают какого-то либо способа решения этой проблемы, поэтому мы в своих исследованиях в области СГМ должны с осторожностью оценивать надежность неожиданных находок. И необходимо помнить о том, что чем меньше объем выборки, тем более вероятно появление ложных результатов. Сравнение двух групп. Критерий Стьюдента или t-критерий. В. Госсет – английский статистик, известный под псевдонимом Стьюдент придумал t-критерий для сравнения двух средних. Парный двухвыборочный t-тест для средних Стьюдента используется для проверки гипотезы о равенстве средних для двух выборок из одной генеральной совокупности. При этом равенство дисперсий не предполагается. При такой организации выборок возможна корреляционная зависимость выборочных случайных величин X и Y. Для оценки этих случайных величин рассчитывают выборочный коэффициент корреляции. Берутся две группы (два столбца) цифр. Как разумно сравнить эти две группы? Подход состоит в том, чтобы сравнить описательные статистики, средние двух групп (выявляется различие между средними двух выборок). Нормируется разность средних двух выборок (групп данных) и делится на корень квадратный из вариации. Обобщение t-критерияна три и более групп данных приводит к дисперсионному анализу (в английской терминологии АNOVA – сокращение от Analysis of Variation – Дисперсионный анализ) и многомерному отклику (MANOVA). Таким образом, методы дисперсионного анализа позволяют разумным образом сравнить групповые средние, если количество групп больше двух. Т-критерий для независимых выборок. Чтобы применить t- критерий для независимых выборок, требуется, по крайней мере, одна независимая (группирующая) переменная и одна зависимая переменная (например, тестовое значение некоторого показателя, которое сравнивается в двух группах). Применение t- критерия неоправданно, если значения двух переменных несопоставимы. Цифры должны быть сопоставимыми (если они несопоставимы, то высокозначимые значения t- критерия могут быть получены искусственно, за счет изменения единиц измерения; аналогично не имеет смысла сравнивать цифры, такие, например, как доходы в рублях от применения целевых программ При сравнении средних можно применять такие графики, как, например, категоризованная диаграмма размаха. Если условия применимости t- критерия не выполнены, то можно оценить различие между двумя группами данных с помощью подходящей непараметрической альтернативы t-критерию. Формальное определение t-критерия. Формально в случае двух групп (k=2) статистика имеет вид:
где
Если гипотеза: «средние в двух группах равны» - верна, то статистика Большие по абсолютной величине значения статистики С помощью вероятностного калькулятора STATISTICA найдем 100 α/2%- ю точку распределения Стьюдента с Обозначим найденную точку через t (α/2). Если Большие абсолютные значения статистики Стьюдента Статистический критерий равенства или однородности дисперсии двух нормальных выборок основан на статистике:
которая при гипотезе: «дисперсии в двух группах равны» имеет распределение Зададимся уровнем значимости С помощью вероятностного калькулятора вычислим 100 (1- Если Т-критерий для зависимых выборок. Степень различия между средними в двух группах зависит от внутригрупповой вариации (дисперсии) переменных. В зависимости от того, насколько различны эти значения для каждой группы, «грубая разность» между групповыми средними показывает более сильную или более слабую степень зависимости между независимой (группирующей) и зависимой переменными. Т-критерий для зависимых выборок имеет преимущества отсеивать дублируемую информацию. Какие можно решить вопросы с помощью Т-критерия для зависимых выборок? Например, различается ли коэффициент общей смертности у мужчин и женщин или на различных территориях? Изучение результатов. Самым быстрым способом изучения таблицы результатов является просмотр столбца, содержащего р -уровни и определение того, какие из р -значений меньше установленного уровня значимости 0,05. Множественные сравнения. Критерий Стьюдента может быть использован для проверки гипотезы о различии средних только для двух групп. Методы множественного сравнения позволяют провести сравнение большего количества групп. Среди параметрических критериев этой группы наиболее известны дисперсионный анализ, критерий Стьюдента для множественных сравнений, критерий Ньюмена-Кейлса, критерий Тьюкки, критерий Шеффе, критерий Даннета, а среди непараметрических – критерии знаков или парного теста Вилкоксона, критерий Краскела-Уоллиса, медианный критерий. К применению этих критериев нужно обращаться в том случае, если дисперсионный анализ показал наличие значимых различий между сравниваемыми значениями выборок. Можно также использовать и другие критерии, такие, как критерий Колмогорова-Смирнова, ранговые критерии Манна-Уитни, Вальда-Вольфовица. Помимо непарметрических критериев различия к непараметрическим методам относятся методы вычисления непараметрических коэффициентов взаимосвязи - коэффициентов ранговой корреляции Спирмена и Кендэла. Непараметрические методы позволяют охарактеризовать одну совокупность, доказать существенность различий двух каких-либо совокупностей, а также исследовать связь между двумя какими-либо признаками. Важной особенностью их является то, что они могут быть использованы при анализе качественных данных. Дисперсионный анализ – это статистический метод, предназначенный для выявления влияния отдельных факторов на результат эксперимента. Он применяется, когда необходимо оценить степень воздействия изучаемых факторов на измеряемые данные, понять, существенно оно или нет. Основной целью дисперсионного анализа является проверка статистической значимости различия между средними двух и более выборок данных. Если вы просто сравниваете средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий. Проверка статистической значимости различия проводится с помощью разбиения суммы квадратов на компоненты, т.е. с помощью разбиения общей дисперсии (вариации) на части, одна из которых обусловлена случайной ошибкой (то есть внутригрупповой изменчивостью), а вторая связана с различием средних значений. Дисперсия – это мера изменчивости признаков: D = Наиболее часто в медицинских исследованиях применяется однофакторный дисперсионный анализ, позволяющий сравнивать между собой несколько независимых выборок. При этом проверяется возможность объединения групп наблюдений, сделанных на различных объектах, в одну общую совокупность. Существуют и другие методы дисперсионного анализа, оценивающего влияние трех, четырех факторов, их совместное влияние (взаимодействие) и т.д. Применение многофакторного дисперсионного анализа позволяет учесть влияние отдельных факторов и их совместное действие как результирующий признак (синергизм, антагонизм). Корреляционный анализ. Научное информационно - аналитическое обеспечение для разрабатываемой системы мероприятий по охране среды обитания и здоровья населения является многоступенчатым процессом, в котором корреляционный анализ занимает одно из ключевых звеньев. Однако, считая, что такой анализ является только лишь инструментом для логических построений и выводов, понимая всю условность математических корреляционных связей между дискретными показателями временных динамических рядов, берутся только те из них, которые обладали высокой степенью достоверности. От английского correlation – согласование, связь, взаимосвязь, соотношение, взаимозависимость, термин впервые введен Гальтоном (Galton) в 1888 г. Корреляция описывает связь между переменными. Корреляционная зависимость отличается по форме, направлению и силе связи. Парная корреляция – между парой переменных. Если исследуется зависимость между двумя переменными, измеренными в интервальной шкале, наиболее подходящим коэффициентом будет коэффициент корреляции Пирсона r (Pearson, 1986), называемый также линейной корреляцией, так как он отражает степень линейных связей между переменными. Сила связи определяется степенью корреляции (таблица № 8). Коэффициент парной корреляции изменяется в пределах от –1 до +1. Крайние значения имеют особенный смысл. Значение –1 означает полную отрицательную зависимость, значение +1 означает полную положительную зависимость, иными словами, между наблюдаемыми переменными имеется точная линейная зависимость с отрицательным или положительным коэффициентом: Таблица № 8 Определение степени корреляционных зависимостей
Значение 0,00 интерпретируется, как отсутствие корреляции. Корреляция определяет степень, с которой значения двух переменных пропорциональны друг другу. Это можно проследить, анализируя графики. Чем ближе коэффициент корреляции к крайнему значению 1, тем теснее группируются данные вокруг прямой. При отрицательных значениях корреляции наклон прямой, вокруг которой группируются значения переменных – отрицательный. При значении коэффициента корреляции, равном ± 1 точки ложатся на прямую линию, а это значит, что между данными имеется точная линейная зависимость. Говорят, что две переменные положительно коррелированы, если при увеличении значений одной переменной увеличиваются значения другой переменной. Две переменные отрицательно коррелированы, если при увеличении одной переменной другая переменная уменьшается. Корреляция высокая, если на графике зависимость между переменными можно с большой точностью представить прямой линией (с положительным или отрицательным наклоном). Если коэффициент корреляции равен 0, то отсуствует четкая тенденция в совместном поведении двух переменных, точки располагаются хаотически вокруг прямой линии. Коэффициент корреляции - безразмерная величина и не зависит от масштаба измерения. Проведенная прямая, вокруг которой группируются значения переменных, называется прямой регрессии, или прямой, построенной методом наименьших квадратов. Формально коэффициент корреляции
R12 = r (Yı, Y₂) =
где Если требуется измерить связи между списками переменных, используются следующие типы корреляции: - множественные корреляции: измерение зависимости между одной переменной и несколькими переменными; - каноническая корреляция: измерение зависимостей между двумя множествами переменных; - частные корреляции. Если вычисляется корреляция между одной переменной, сдвинутой на некоторый лаг, то говорят об автокорреляции. Перспективность применения корреляционного анализа в СГМ заключается в том, что он позволяет устанавливать подобие санитарно-гигиенических ситуаций в динамике, определять степень схожести в этой области знаний и узнавать ситуации по комплексу показателей. Корреляционно-регрессионный анализ. Идея коэффициента Спирмена проста. Анализируемые переменные ранжируются. Затем вместо самих значений берутся ранги и рассчитывается коэффициент ранговой корреляции Спирмена. Если анализируемые признаки взаимосвязаны, изменения их числовых значений в большую или меньшую сторону будут совпадать, соответственно разность их рангов будет минимальна и наоборот. Коэффициенты корреляции рангов применяются для оценки связи между подобного рода признаками. Применение коэффициентов ранговой корреляции может быть рекомендовано в случаях: необходимости быстро ориентировочно определить связь между какими-то признаками; определить связь между качественными или количественными признаками или только между качественными признаками; когда распределение значений учетных признаков не соответствует нормальному распределению или распределение неизвестно, при небольшом числе наблюдений сравниваемых пар признаков. Существует несколько вариантов вычисления коэффициентов ранговой корреляции. Коэффициент корреляции Спирмена (rs) может рассчитываться по формуле:
где d – разность между рангами по двум переменным; N – число сопоставляемых пар. Оценка надежности коэффициента корреляции рангов Спирмена проводится с помощью критерия t. Критерий Краскала-Уоллиса используется для оценки различий одновременно между более чем двумя выборками по уровню какого либо признака. Данный критерий позволяет установить, что уровень признака изменяется при переходе от группы к группе, но не указывает на направление этих изменений. Он рассматривается как непараметрический аналог метода дисперсионного однофакторного анализа для несвязанных выборок. Данный метод может быть представлен формулой:
n – количество испытуемых с оцениваемым признаком в каждой группе. Дескриминантный анализ – это раздел многомерного статистического анализа, занимающийся решением задач классификации (распознавания образов) и внесением объектов с определенным набором признаков (симптомов) к одному из известных классов. При дискриминантом анализе определяют, к какой из нескольких возможных генеральных совокупностей принадлежит объект, случайно взятый из одной среди них. При решении задач медицинской диагностики дискриминантный анализ выполняется в 3 этапа. Первый этап – формируется обучающая выборка. Каждый объект характеризуется множеством признаков (показатели качества воды) и достоверно установленным фактом принадлежности к одному из дифференцируемых слагающих (например, одна территория). Второй этап – вырабатываются решающие правила и дается оценка их информативности. Третий этап – отнесение объекта к определенному классу, группе. Кластерный анализ. Термин кластерный анализ в действительности включает в себя набор различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры. В общем, всякий раз, когда необходимо классифицировать "горы" информации к пригодным для дальнейшей обработки группам, кластерный анализ оказывается весьма полезным и эффективным. Цель алгоритма объединения объектов исследования при классификации состоит в объединении объектов (например, административных округов города) в достаточно большие кластеры, используя некоторую меру сходства или расстояние между объектами. Типичным результатом такой кластеризации является иерархическое дерево. Ранг и персентиль. Используется для вывода таблицы, содержащей порядковый и процентный ранги для каждого значения в наборе данных. Данный инструмент располагает исходные данные в порядке возрастания рангов. При этом наибольшему значению присваивается первый ранг, следующему – второй и т.д. Указывается также порядковый номер точки в исходных данных. Для каждого значения исходных данных рассчитывается процент, при этом наибольшему значению (первому рангу) соответствует 100%, а наименьшему значению (наибольшему рангу) соответствует 0%. Скользящее среднее. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее - начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
где yi – фактическое значение i -го уровня; m – число уровней, входящих в интервал сглаживания (m=2p+l); yt - текущий уровень ряда динамики; i – порядковый номер уровня в интервале сглаживания; p - при нечетном m
Интервал сглаживания, т.е. число входящих в него уровней m определяют, используя следующее правило: если необходимо сгладить мелкие, беспорядочные колебания, то интервал сглаживания берется по возможности большим; если же нужно сократить более мелкие волны и освободиться от периодически повторяющихся колебаний – интервал сглаживания уменьшают. В пакете Анализ данных инструмент Скользящее среднее использовалось для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного из предшествующих периодов. Работа пакета анализа по определению скользящей средней ряда динамики включал себя нижеследующее. В категории Входные данные указывались значения параметра Интервал (число уровней m, входящих в интервал сглаживания).
∆ t+2p =
Сортировка (по убыванию и возрастанию). Преимущества метода сортировки в программе Statistica 6.0 перед методом распределения «ранги и персентили» в пр. Excel: - можно обрабатывать данные сплошного массива за многолетние периоды; за 2-3 и сколь угодно многолетних периода или группам территорий и пр. в сравнении; - быстрота и удобство. Экспоненциальное сглаживание. Э кспоненциальное сглаживание используется для выравнивания временных рядов. Его особенность заключается в том, что в процедуре нахождения сглаженного уровня используются значения только предшествующих уровней ряда, взятые с определенным весом, причем вес наблюдения уменьшается по мере удаления его от момента времени, для которого определяется сглаженное уровня ряда. Если для исходного временного ряда y1, y2….., yn соответствующие сглаженные значения уровней обозначить S1, t=1, 2, …., n, то экспоненциальное сглаживание осуществляется по формуле
Величина параметра сглаживания бралась в интервале от 0,1 до 0,3. Однако, можно определять величину α исходя из длины сглаживаемого ряда: α Что касается начального параметра S1, то в конкретных задачах его берут или равным значению первого уровня ряда y1, или равным средней арифметической нескольких первых членов ряда, например S1= Указанный порядок выбора величины S1 обеспечивает хорошее согласование сглаженного и исходного рядов для первых уровней. Если при подходе к правому концу временного ряда сглаженные этим методом значения при выбранном параметре α начинают значительно отличаться от соответствующих значений исходного ряда, необходимо перейти к другому параметру сглаживания. При этом методе сглаживания не теряются ни начальные, ни конечные уровни сглаживаемого временного ряда. При необходимости рассчитываются стандартные погрешности сглаживаемого ряда. Искусственные нейронные сети (нейрокомпьютинг). Под искусственной нейронной сетью (ИНС) понимается система обработки информации, основанная на моделировании функций мозга. Основополагающий принцип, положенный в основу ИНС – это сходство их строения и функционирования с биологическим прототипом – нервной системой живых организмов [ 6 ].. Основным структурным элементом ИНС является искусственный нейрон, выходной сигнал которого вычисляется, как пороговая или сигмоидная функция от взвешенной суммы входных сигналов Главной качественной особенностью ИНС является то, что они могут быть настроены на некоторое правило обработки информации без явного его задания, но путем обучения по эталонам типа «входной сигнал - выходной сигнал», «ситуация - действие». В исследовании, с помощью универсального пакета нейросетевого анализа Statistica Neural Networks фирмы StatSoft (США), может быть использована общая структура нейросетевой модели (НС-модели) в виде 3-слойной нейронной сети (многослойный персептрон), эмулируемой на персональном компьютере. ИНС параметризована двумя матрицами весовых коэффициентов: A – размерами p
где Х – вектор входных сигналов.
Рисунок № 5. Строение нейронной сети. АВС-логистический анализ
С помощью такого анализа в программе Exel можно проводить рейтинговое распределение показателей [3, 5, 9].Например, рейтинговое распределение территорий по показателям общей смертности и общей заболеваемости населения. Методика АВС-логистического анализа строится по следующей схеме действий: 1) определяется сумма всех показателей (в нашем случае - сумма коэффициентов смертности или заболеваемости в перерасчете абсолютных цифр на 1000 и 100000, соответственно); 2) каждый отдельный показатель делим на полученную сумму и получаем процентный ранг (сумму вклада); 3) через «окно данных» сортируем вклад (каждого показателя) по мере убывания; 4) делаем нарастающую сумму рангов (предыдущий результат плюс последующий); 5) для наглядности введем 10 рейтингов - 100-90% = 10 рейтинг - наивысший неблагоприятный среди территорий; 90-80% = 9 рейтинг - высший неблагоприятный; 80-70% = 8 рейтинг - высший неблагоприятный; 70-60% = 7 рейтинг - неблагоприятный; 60-50% = 6 рейтинг – неблагоприятный; 50-40% = 5 рейтинг – неблагоприятный; 40-30% = 4 рейтинг – ниже неблагоприятного; 30-20% = 3 рейтинг – значительно ниже неблагоприятного; 20-10% - 2 рейтинг – значительно ниже неблагоприятного; 10-0% - 1 рейтинг – благоприятный среди территорий. Результаты исследований можно оформить графически, по суммарным рейтингам – сумме коэффициентов по отдельным территориям за все годы. Существует несколько разновидностей АВС-анализа. В частности, такой логистический метод, как предварительное составление графика системы профилактических мероприятий по результатам исследований. При этом все мероприятия по приоритетности предварительно целесообразно разбить на 3 группы. Группа А – наиболее ценные, на их долю приходится около 80% стоимости всей системы. Группа В – средние по стоимости и значимости (примерно 10 – 15%). Группа С – наименее значимые (5 – 10%). Анализ кривой АВС показывает, что группа мероприятий А должна находиться под строгим контролем и учетом, эти мероприятия – основные. Мероприятия, относящиеся к группе В, требуют обычного контроля, налаженного учета и постоянного внимания. Мероприятия, относящиеся к группе С, нуждаются в обычном контроле (периодические проверки).
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 2423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.017 с.) |

 ,
, и
и  - выборочные средние первой и второй выборки,
- выборочные средние первой и второй выборки,  - оценка дисперсии, составленная из оценок дисперсий для каждой группы данных:
- оценка дисперсии, составленная из оценок дисперсий для каждой группы данных: ;
;
 имеет распределение Стьюдента с
имеет распределение Стьюдента с  степенями свободы.
степенями свободы. степенями свободы.
степенями свободы. , то гипотеза отвергается.
, то гипотеза отвергается. могут возникнуть как из-за значимого различия дисперсий сравниваемых групп.
могут возникнуть как из-за значимого различия дисперсий сравниваемых групп. ,
, .
.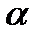 .
. / 2)% и 100 (1-
/ 2)% и 100 (1-  , то гипотеза об однородности дисперсии не отвергается.
, то гипотеза об однородности дисперсии не отвергается. . Под вариацией здесь понимают сумму квадратов отклонений относительно выбранного среднего значения:
. Под вариацией здесь понимают сумму квадратов отклонений относительно выбранного среднего значения:  .
. Пирсона между переменными Yı, Y₂вычисляется следующим образом:
Пирсона между переменными Yı, Y₂вычисляется следующим образом: ,
, - среднее переменной
- среднее переменной  ,
,  - среднее переменной
- среднее переменной  .
.


 .
. Вывод графика и вывод Стандартных погрешностей в программе Excel, которые рассчитываются по формуле:
Вывод графика и вывод Стандартных погрешностей в программе Excel, которые рассчитываются по формуле: .
. .
. .
. , где
, где  - весовые коэффициенты, x – входные сигналы. Из подобных структурных элементов, искусственных нейронов, сгруппированных по слоям, состоит нейронная сеть (рисунок № 5).
- весовые коэффициенты, x – входные сигналы. Из подобных структурных элементов, искусственных нейронов, сгруппированных по слоям, состоит нейронная сеть (рисунок № 5). (n+1) и B – размерами k
(n+1) и B – размерами k  ,
,  ,
,  ,
,  ,
, – логистическая функция
– логистическая функция  ;
;


