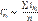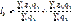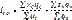Понятие о статистической сводке и группировке. Виды статистических группировок.

Понятие и виды средних величин

Средняя величина - обобщающая характеристика изучаемого признака в исследуемой совокупности, отражающая его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.

Существует две категории средних величин:

1) степенные средние;

2)структурные средние.

Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.

Простая средняя рассчитывается по несгруппированным данным.

Взвешенная средняя рассчитывается по сгруппированным данным.

m – показатель степенной средней, x_i – варианты, f_i – частоты.

В зависимости от того, какое значение принимает показатель степени (m) различают следующие виды степенных средних:

Вид степенной средней	Показатель степени	Формула расчета
Простая	Взвешенная
Гармоническая	-1
Геометри- ческая
Арифметическая
Квадратическая

 

Средняя арифметическая: сущность, свойства, методика расчета

Под средней арифм. понимается такое знач. признака,которое имела бы каждая единица совокупности, если бы общий итог всех знач.признака был распределен равномерно между всеми единицами совокупности.

В интервальных рядах распределения для расчета средней прежде всего определяют середины интервалов, они и будут значениями х.

Свойства средней арифметической:

1) средняя арифм. постоянной величины равна этой постоянной;

2) произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты;

3) сумма отклонений индивидуальных значений признака от средней арифметической равна нулю;

4) сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины А;

5) если все осредняемые варианты увеличить или уменьшить на постоянное число А, то средняя арифметическая соответственно увеличится или уменьшится на ту же величину.

На изложенных свойствах средней арифметической базируется один из методов ее расчета – способ моментов

∑(х_i-x₀) *f_i

h

m₁= --------------

∑f_i

h – величина интервала, х₀ – значение середины интервала, находящегося в центре ряда

Средняя гармоническая: сущность методика расчетов

Средняя гармоническая является преобразованной формой средней арифметиче-ской и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений при-знака, скрытые в весах средней гармонической.

Если в исходных данных имеются значения осредняемого признака (х) и объем ос-редняемого признака (w), то для расчета средней применяется гармоническая взвешен-ная. Среднюю гармоническую применяют, когда в качестве весов применяются не еди-ницы совокупности, а произведения этих единиц на значения признака.

Понятие о выборочном наблюдении и определение ошибок выборк

Выборочным -наблюд, при кот. хар-ка всей сов-ти единиц дается по некоторой их части, отобранной в случайном порядке.

Вся сов.единиц наз-ся генеральной сов-тью(N). Отобранная из ген.совокупности часть единиц, подвергающаяся обследованию, называется выборочной сов., или выборкой (ее численность обозначается n).Задача выб.наблюд.-получить правильное представление о показателях всей ген.сов-ти на основе изучения выборочной совокупности.

Сред.значение призн. в ген.совокупности может быть определено:

Среднее значение признака в выборочной совокупности определяется:

Дисперсия признака определяется:

- генеральная дисперсия

- выборочная дисперсия

Дисперсия доли:

- генеральная дисперсия доли

- выборочная дисперсия доли

Определение ошибок выборки

О.в.-возможные пределы отклонений выборочных характеристик от генеральных характеристик.

Различают систематические и случайные ошибки репрезентативности.

Различают среднюю и предельные ошибки выборки, к-ые связаны след. соотношением: ∆ = t*μ

В завис-ти от метода (повторного или бесповторного) средняя ошибка рассчит-ся

Конечная цель выборочного наблюдения состоит в определении генеральной характеристики средней доли на основе расчета выборочных характеристик и ошибки выборки поскольку между ними существует следующая зависимость:

Изучение сезонных колебаний

Сезонными колебаниями-более или менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений.

При статистическом изучении сезонных колебаний решаются две взаимосвязанные задачи:

1) выявление специфики развития во внутригодовой динамике;

2) измерение сезонных колебаний изучаемого явления с построением модели сезонной волны.

Для выявления сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за несколько лет.

Измерение сезонных колебаний осуществляется с помощью расчета индексов сезонности, которые показывают, во сколько раз фактический уровень ряда в момент или интервал времени t больше среднего уровня либо уровня, вычисляемого по уравнению тенденции.

Вычисленные средние индексы сезонности свободны от влияния основной тенденции развития и случайных отклонений.

В зав-ти от характера тренда формула принимает следующий вид:

1) для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития

Измерение сезонных колебаний на базе переменных уровней тренда называется способом переменной средней;

2) для рядов внутригодовой динамики, в которых повышающийся (снижающийся) тренд отсутствует или он незначителен

Поскольку для всех эмпирических уровней анализируемого ряда динамики этот общий средний уровень является постоянной величиной, то применение формулы называется способом постоянной средней.

Индекс Ласпейреса

При сравнении числителя и знаменателя формулы определяется показатель прироста товарооборота при продаже товаров в базисном периоде по цена текущего периода:

Средние индексы

Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов.

Средние общие индексы получают путем преобразования агрегатных индексов. Агрегатный индекс может быть преобразован в средний арифметический или средний гармонический. Форму средней нужно выбрать таким образом, чтобы полученный средний индекс был тождественен исходному агрегатному индексу. Средний арифметический индекс тождественен агрегатному индексу если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Средний гармонический индекс тождественен агрегатному, если весами индивидуальных индексов будут слагаемые числителя агрегатного индекса.

Средние индексы применяют, если не известны значения отдельных и индексируемых явлений и их весов в отчетном или базовом периодах, но известны их изменения, которые могут быть представлены в виде индивидуальных индексов. Таким образом, если анализируется изменение объема, то пользуются обычно среднеарифметическим взвешенным индексом, например:

Если анализируется изменение качественного показателя, то обычно используется среднегармонический индекс, например, индекс себестоимости:

Индексы средних величин

При анализе изменения средних уровней пользуются индексами переменного, постоянного состава и структурных сдвигов. Например:

- индекс переменного состава (индекс средней себестоимости):

- индекс постоянного состава (индекс изменения себестоимости отдельных элементов совокупности):

- индекс структурных сдвигов:

24. Виды и формы взаимосвязи между явлениями

Связи между признаками и явлениями классифицируются по ряду оснований:

1) по степени зависимости одного явления от другого различают функциональную и стохастическую связь.

Функциональной называется связь, при которой определенному значению фактор-ного признака соответствует одно строго определенное значение результативного при-знака. Наиболее часто функциональные связи проявляются в естественных науках, на-пример, в механике функциональной является зависимость расстояния, пройденного объектом, от скорости его движения.

Стохастической называется связь, при которой каждому значению признака х со-ответствует множество значений признака y. Статистическая связь проявляется лишь «в общем и среднем» при большом числе наблюдений за явлением.

Корреляционной является статистическая связь между признаками, при которой изменение значений независимой переменной X приводит к закономерному изменению математического ожидания случайной величины Y.

2) по направлению различают прямую и обратную связь.

Прямой называется связь, при которой с ростом значений факторного признака возрастают значения результативного признака.

При обратной связи с увеличением значения одного признака величина другого признака, зависящего от него, уменьшается.

3) по аналитическому выражению различают линейные и нелинейные связи.

Линейная – связь, которая может быть аналитически выражена уравнением пря-мой линии.

Нелинейная (криволинейная) – связь, которая может быть выражена уравнением какой-либо кривой.

25. Способы выявления и хар-ки взаимосвязей

Для выявления наличия связи, ее характера и направления в статистике использу-ются следующие методы:

1)метод сопоставления параллельных рядов. При этом методе данные сопоставля-ются обычно в табличной форме в виде параллельно расположенных стат. рядов. Значе-ние факторного признака располагается в возрастающем порядке, параллельно записыв-ся значения результативного признака и путем сопоставления выявляют нали-чие/отсутствие связи.

2)балансовый метод. Данные взаимосвязанных показателей излагаются в виде таб-лиц, в которых итоги отд. частей должны быть равны м/у собой. Этот метод использ-ся для выявления взаимосвязей м/у производством и реализацией использования ресурсов предприятия Он+П=Р+Ок

3)метод аналитических группировок позволяет установить наличие м/у двумя и более признаками взаимосвязь, а также ее направление

4)метод дисперсионного факторного анализа дает возм-ть определить значение систематической и случайной вариацией

5)индексный метод факторного анализа отражает компонентные связи

6)по графическому методу можно определить наличие, направление, форму и силу связи.

7)метод таблиц сопряженности основан на построении таблиц, в к-ых дается ком-бинационное распределение единиц совокупности по 2-м альтернативным признакам.

Оценка существенности связи

Поскольку исходные данные, по которым устанавливается взаимосвязь признаков, являются определенной выборкой из некоей генеральной совокупности объектов, то ис-численные по этим данным парные коэффициенты корреляции будут выборочными. Ес-ли исходные данные точно отражают структуру и закономерности генеральной совокуп-ности, то и исчисленный по ним коэффициент корреляции будет показывать реальную связь, присущую в действительности всей исследуемой совокупности объектов.

Проверка адекватности моделей, построенных на основе уравнений регрессии, на-чинается с проверки значимости каждого коэффициента регрессии. Значимость коэффи-циентов регрессии осуществляется с помощью t-критерия Стьюдента.

Параметр модели признается значимым, если расчетное значение t-критерия боль-ше критического, которое определяют по таблице Стьюдента.

Кроме этого показ-ля может быть рассчитана средняя ошибка аппроксимации. Значение средней ошибки не должно превышать 12-15%.

Стат. изучение рынка труда

Рынок труда– сфера экономики, для которой предметом являются отношения купли-продажи рабочей силы.

Объектом изучения на рынке труда выступают трудоспособное население и трудо-вые ресурсы.

Трудоспособное нас.–совокупность людей, способных к труду по возрасту и сост.здоровья. В соответствии с зак.трудоспособным считается возраст для мужчин – от 16 до 59 лет и для женщин – от 16 до 54 лет включительно.

Нас.в труд.возрасте состоит из трудоспособного населения и на-селения, нетрудоспособного по состоянию здоровья. В последнюю группу включаются неработающие инвалиды 1 и 2 групп рабочего возраста, а также неработающие пенсио-неры трудоспособного возраста, получающие пенсию по возрасту на льготных условиях.

Трудовые ресурсы - часть населения страны, которая фактически занята в экономи-ке или же не занята, но способна к труду по возрасту и состоянию здоровья.

К трудовым ресурсам относятся:

1)трудоспособное население в трудоспособном возрасте;

2)фактически работающие подростки моложе 16 лет;

3)фактически работающие лица старше трудоспособного возраста.

Методы расчета численности трудовых ресурсов:

1)демографический (по источникам формирования)

2)экономический (по фактической занятости)

Естественное пополнение трудовых ресурсов (ПТРе) происходит за счет вступле-ния в трудоспособный возраст подростков, а также за счет привлечения к общественно-му труду пенсионеров и лиц в возрасте до 16 лет.

Естественное выбытие (ВТРе) трудовых ресурсов происходит за счет смертно-сти, перехода на пенсию или инвалидность, прекращения работать лицами нетрудоспо-собного возраста.

Естественный прирост трудовых ресурсов – это разность между естественным пополнением и естественным выбытием трудовых ресурсов.

Под механическим движением трудовых ресурсов понимается изменение их чис-ленности за счет миграции.

Баланс трудовых ресурсов – это система показателей, отражающих численность и состав трудовых ресурсов и их распределение на экономически активное (по отраслям экономики и формам собственности) и экономически неактивное население.

Баланс трудовых ресурсов состоит из двух разделов. В первом разделе показыва-ются источники формирования трудовых ресурсов, во втором – их распределение на за-нятое и незанятое население. В настоящее время баланс трудовых ресурсов составляется по среднегодовым данным.

Понятие о статистической сводке и группировке. Виды статистических группировок.

Сводка представляет собой систематизацию материала о единицах статистической совокупности, собранного и зарегистрированного в ходе статистического наблюдения. Цель сводки - получение обобщающих статистических показателей, характеризующих совокупность в целом.

Различают простую и сложную сводку. Простая сводка предполагает сведение полученных данных в статистические таблицы, подведение общих итогов по совокупности в целом. Сложная сводка осуществляется с применение метода группировок по определенной программе

Группировка – расчленение множества единиц изучаемой совокупности на группы, однородные по какому-либо признаку и характеристика таких групп с помощью системы показателей.

В зависимости от решаемых задач статистические группировки делятся на:

1)типологическая группировка - это разделение исследуемой качественно разнородной совокупности на классы, социально-экономические типы;

2)структурная - группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-либо варьирующему признаку;

3)аналитическая - группировка, производимая с целью выявления взаимосвязей между изучаемыми явлениями и их признаками.

Признаки подразделяются на две группы: факторные и результативные.

Факторные - признаки, под воздействием которых изменяются другие признаки. Зависимый признак называется результативным.

5. Понятие о рядах распределения

Результаты группировки собранных стат.данных представляются в виде радов распределения.

Стат.ряд распред.-это упорядоченное расположение единиц совокупности по варьирующему признаку. Он характеризует состав (структуру) изучаемого явления, позволяет судить об однородности совокупности, границах ее изменения, закономерностях развития изучаемого объекта.

типы рядов распределения:

1)атрибутивные - ряды распред., построенные по качественным признакам;

2)вариационные – ряды распред., построенные по количественному признаку.

Вариационный ряд состоит из двух элементов: вариант и частот.

Варианта – знач., кот. может принимать признак у единиц совокупности.

Частота – кол-во единиц наблюд., обладающих данным значением признака.

Сумма частот всегда равна объему совокупности. Иногда вместо частот рассчитывают частости – это частоты, выраженные било в долях единицы, либо в процентах к объему совокупности.

Вариационные ряды бывают дискретными и интервальными. У дискретных рядов варианты выражены конкретными числами, чаще всего целыми. В интервальных рядах значения показателя задаются в виде интервалов.

Интервалы имеют две границы: нижнюю и верхнюю.

Если признак принимает ограниченное число значений, обычно не больше 10, строят дискретные ряды распределения. Если вариант больше, то дискретный ряд теряет свою наглядность; в этом случае целесообразно использовать интервальную форму вариационного ряда.

Представленные без какой-либо систематизации данные образуют первичный ряд. Ранжированный ряд предполагает расположение всех вариантов ряда в возрастающем (или убывающем) порядке.

6. Понятие абсолютных величин. Единицы измерения абсолютных величин.

Абсолютные показатели отражают физические размеры изучаемых статистикой процессов и явлений, а также могут представлять объем совокупности.

Сводные объемные показатели, получаемые в результате сводки и группировки, характеризуют объем признака или объем совокупности как в целом по изучаемому объекту, так и по какой-либо его части.

В зависимости от социально-экономической сущности исследуемых явлений, их физических свойств они выражаются в натуральных, стоимостных или трудовых единицах измерения.

Натуральные единицы измерения могут быть:

а) простые;(кг,м,м2,м3)

б) комбинированные (сложные);(т/кг, квт/ч)

в)условно-натуральные единицы применяются при характеристике потребления различных видов топлива в пересчете на условное топливо.

Стоимостные единицы измерения используются при обобщении учетных данных. Они дают денежную оценку социально-экономическим явлениям и процессам.

Трудовые единицы измерения позволяют учитывать общие затраты труда на предприятии, а также трудоемкость отдельных операций технологического процесса.

 

7. Относительные величины, их сущность и формы выражения. Виды относительных величин, методы расчета.

Относительная величина - величина, полученная в резуль.деления одного абсолютного показателя на др.и выражающая соотношение между количественными характеристиками социально-экономических явлений и процессов.

Виды относительных величин:

1. От.величина выполнения плана –отнош.фактически достигнутого уровня (У₁) к запланированному на тот же период (У_пл):

2. Отн. величина планового задания-отношение уровня запланированного на предстоящий период (У_пл) к уровню показателя фактически достигнутого в предыдущем периоде (У₀):

3. Отн.и величинами динамики показатели, выражающие степень изменения явлений во времени. ОВД=ОВПЗ*ОВВП

4. От.величины структуры (ОВС) представляют собой отношение размеров частей и целого.

ОВС= y_i/∑y_i

5. От.величинами координации называют соотношение частей целого между собой.

ОВК=y_i/y_j

6. От. величинами интенсивности (ОВИ) называют относительные величины, характеризующие распространение, развитие какого-либо явления в определенной средe.

ОВИ = показ-ль, харак-щий явл-е А

показ-ль, харак-щий среду распростр-я явл-я А

7. От.показатель сравнения (ОПСр) опред.соотношение одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, фирмы, края, области страны и т.д.).

ОВС= показ-ль, харак-щий объект А

показ-ль, харак-щий объект В