
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Статистическое изучение связи между явлениямиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Справочные материалы Виды и формы связей, различаемые в статистике. При исследовании социально-экономических явлений часто приходится иметь дело с взаимосвязанными показателями. Типы взаимосвязей по характеру зависимости, различаемые в статистике, представлены на схеме 8.1.
Схема 8.1.Типы взаимосвязей по характеру зависимости
Взаимосвязи можно классифицировать также следующим образом (схема 8.2):
Схема 8.2. Классификация связей
Для анализа статистических зависимостей на начальной стадии применяются методы, представленные на схеме 8.3.
Схема 8.3. Начальная стадия анализа статистических зависимостей
Пример 8. 1. Имеются данные о выпуске продукции на 6 однотипных предприятиях (х) и потреблении на них электричества (у) (таблица 8.1.): Таблица 8.1. Зависимость потребления электричества от объема выпуска продукции
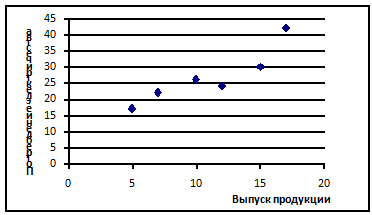
Сделать вывод о наличии, характере и форме связи. Решение: Поле корреляции построено на рис. 8.1.
Рисунок 8.1. Зависимость потребления электричества от выпуска продукции Таблица и рисунок демонстрируют, что с увеличением факторного признака х увеличивается результативный признак у, следовательно связь между ними можно считать прямой.
Пример 8. 2. Метод аналитических группировок продемонстрируем на примере таблицы 8.2.: Таблица 8.2. Характеристика зависимости прибыли малых предприятий от оборачиваемости оборотных средств за 2003 год
Графический метод демонстрируется на рисунке 8.2. Построив график, можно судить о форме связи, ее направлении, а по разбросу точек – о тесноте связи (отсутствие связи будет характеризоваться разбросанностью точек по всему графику).
Рис. 8.2. Графики поля корреляции Измерение тесноты связи в случае корреляционной зависимости. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (при изучении множественных зависимостей) факторных признаков.
Простейший показатель тесноты связи - показатель Фехнера.
где C – совпадения знаков отклонений Н – несовпадения знаков отклонений
Мера совместной вариации признаков - коэффициент ковариации.
Показатель интенсивности линейной связи – линейный коэффициент парной корреляции Пирсона (коэффициент корреляции).
Путем ряда преобразований можно получить следующие аналитические выражения для расчета линейного коэффициента корреляции.
где
Показатель Фехнера и коэффициент корреляции Пирсона изменяются в пределах [-1;+1].
Пример 8.3. Измерим тесноту связи с использованием формул (8.1) - (8.3) по данным примера 8.1. Решение: 1) Расчет показателя Фехнера Рассчитаем средние значения для х и у:
Показатель Фехнера 2) Расчет коэффициента ковариации
3) Расчет линейного коэффициента корреляции: С учетом того, что Полученные значения показателя Фехнера и коэффициента корреляции свидетельствуют о достаточно сильной прямой связи.
На прямую или обратную связь указывает знак коэффициента («+» или «–» соответственно). О тесноте связи свидетельствует абсолютная величина коэффициента. Для качественной оценки тесноты связи используется таблица Чэддока (табл. 8.3.) Таблица 8.3. Критерии оценки тесноты связи (шкала Чеддока)
Оценка достоверности коэффициента корреляции. Для более наглядного представления об оценке достоверности (значимости) коэффициента корреляции построена таблица 8.4.
Таблица 8.4. Оценка достоверности (значимости) коэффициента корреляции
Доверительные границы коэффициента корреляции рассчитываются как:
где ρ – генеральное значение коэффициента корреляции; tp – заданный уровень вероятности.
Пример 8.4. Проверить значимость коэффициента корреляции, рассчитанного по данным примера 8.1. Решение:
Ранговая корреляция. В анализе социально-экономических явлений широко используются ранговые коэффициенты корреляции (коэффициенты корреляции рангов), когда коррелируют не непосредственные значения X и Y, а их ранги, т.е. номера их мест, занимаемых в каждом ряду значений по возрастанию или убыванию. К таким непараметрическим коэффициентам относятся коэффициенты рангов Спирмена и Кендэлла. Коэффициент ранговой корреляции Спирмена:
Значимость коэффициента ранговой корреляции Спирмена:
Коэффициент корреляции Спирмена считается статистически значимым, если
Пример 8.5. Имеются данные о затратах на рекламу продукции и объеме выручки от реализации продукции (табл. 8.5.; графы А и Б). Таблица 8.5. Зависимость затрат на рекламу продукции и объема выручки от реализации продукции
Вычислить коэффициент Спирмена. Решение: Определив ранги значений X и Y и их разность (табл. 8.5.; графы 1, 2, 3, 4), получаем При условии, что ранги не повторяются, коэффициент ранговой корреляции Кендэлла рассчитывается как:
где S – фактическая сумма рангов При этом соблюдаем следующую последовательность действий: 1. Значения Х ранжируются в порядке возрастания или убывания. 2. Значения У располагаются в порядке соответствующем значениям Х. 3. Для каждого ранга У определяется число следующих за ним значений рангов, превышающих его величину. Результат записывается в столбец «+», суммируется и обозначается Р. 4. Для каждого ранга У определяется число следующих за ним меньших значений рангов. Результат записывается в столбец «–», суммируется и обозначается Q. 5. Определяется общая сумма S = P+Q.
Интерпретация коэффициентов Спирмена и Кендэлла аналогична интерпретации коэффициента корреляции Пирсона.
Пример 8.6. Рассчитаем значение коэффициента Кендэлла на основании данных примера 8.5 Решение:
5-й шаг: S=P+Q=32+(-13)=19, тогда
Существенность коэффициента корреляции рангов Кэндэлла проверяется по формуле:
где
Коэффициент Кендэлла всегда меньше по значению, чем коэффициент Спирмена, точнее
Если отдельные значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяются. Данные ранги называются связанными (или повторяющимися). Для случая связанных рангов есть особые скорректированные формулы для коэффициентов Спирмена и Кендэлла, однако на практике часто пользуются формулами приведенными выше.
Корреляция альтернативных признаков
Для исследования степени тесноты связи между качественными признаками могут быть использованы коэффициенты контингенции Пирсона, ассоциации Юла и взаимной сопряженности Пирсона. В том случае, когда качественные признаки представлены в виде альтернативных (дихотомических), рассчитываются коэффициенты контингенции и ассоциации на основе четырехклеточных таблиц следующего вида:
Коэффициент контингенции:
Коэффициент ассоциации:
Значимость коэффициента ассоциации проверяется следующим образом:
Коэффициент ассоциации считается статистически значимым, если
Пример 8.7. В результате обследования работников предприятия получены следующие данные (чел.)
Требуется оценить тесноту взаимосвязи между уровнем образования и удовлетворенностью работой с помощью коэффициентов контингенции и ассоциации. Решение:
Коэффициенты контингенции и ассоциации изменяются в пределах [-1;+1], но величина коэффициента контингенции для тех же данных по абсолютной величине меньше величины коэффициента ассоциации, т.е
В случае если каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи используют коэффициент взаимной сопряженности Пирсона. Информация для оценки этой связи группируется в виде таблицы (mij – частоты взаимного сочетания двух качественных признаков).
Коэффициент взаимной сопряженности Пирсона определяется по формуле:
где
Интерпретация коэффициентов контингенции, ассоциации и взаимной сопряженности Пирсона аналогична интерпретации коэффициента корреляции Пирсона.
Пример 8.8. Для изучения влияния условий труда на взаимоотношения в коллективе было проведено выборочное обследование 250 работников предприятия, ответы которых распределились следующим образом:
Рассчитать коэффициент взаимной сопряженности Пирсона. Решение:
Множественная корреляция. Изменение экономических явлений происходит под влиянием не одного, а большого числа различных факторов. Для измерения тесноты корреляционной связи между результативным признаком и несколькими факторными признаками при линейной форме связи рассчитывается коэффициент множественной корреляции. Коэффициент множественной корреляции, для случая двух факторных признаков x1 и x2 рассчитывается по формуле:
Множественный коэффициент корреляции изменяется в пределах [0;1] и численно не может быть меньше, чем любой из образующих его парных коэффициентов. Приближение R к единице свидетельствует о сильной зависимости между признаками. Средняя квадратическая ошибка коэффициента множественной корреляции определяется по формуле:
Тогда, если
Проверка значимости коэффициента множественной корреляции осуществляется так же по F-критерию Фишера. Для случая двух факторных признаков х1 и х2 он имеет вид:
Коэффициент множественной корреляции считается статистически значимым, если В ходе изучения множественной корреляции рассчитывают также частные коэффициенты корреляции. Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками при фиксированном значении всех остальных. Для случая двух факторных признаков x1 и x2 формулы будут иметь вид:
В первом случае исключено влияние факторного признака х2, а во втором х1. Значения парного и частного коэффициентов корреляции отличаются друг от друга, т.к. парный коэффициент характеризует связь между двумя признаками без учета влияния других признаков, а частный учитывает наличие и влияние других факторов.
Проверка значимости и расчет доверительных интервалов для частных коэффициентов корреляции аналогичны, как и для парных коэффициентов корреляции, с тем лишь отличием. Что число степеней свободы n определяется так: n = n - k., где k – порядок коэффициента частной корреляции.
8.2. Домашнее задание к теме 8 1. По следующим данным рассчитайте коэффициент корреляции Пирсона и сделайте выводы:
2. Следующая таблица представляет значения премий, выплаченных десятью страховыми обществами (Х), и их резервы для выплаты непредъявленных премий (Y).
Оценить тесноту связи между выплачиваемыми премиями и резервами страховых обществ.
3. По группе акционерных коммерческих банков региона имеются следующие данные:
Оценить тесноту связи между прибылью и активами банков.
4. По данным аудиторского отчета о деятельности 12 коммерческих банков построена следующая таблица:
Оценить степень тесноты связи между размером кредитной ставки и доходностью кредитных операций.
5. По однородным предприятиям имеются данные о количестве рабочих с профессиональной подготовкой и количестве бракованной продукции:
Рассчитайте линейный коэффициент корреляции и проверьте его значимость.
6. У 8 учащихся колледжа зафиксировано следующее количество баллов, полученных за самостоятельные работы по математике (х) и по гуманитарным предметам (y).
Оценить степень тесноты связи между успеваемостью по математике и гуманитарным предметам.
7. По результатам ранжирования стран по уровню эффективности экономики и степени политического риска, определите коэффициенты ранговой корреляции и сделайте выводы.
8. С помощью ранговых коэффициентов определите, существует ли связь между намерениями учащихся после окончания учебного года в зависимости от пола и от места проживания.
Рассчитайте коэффициенты ранговой корреляции для данных, представленных в таблице. Сделайте выводы.
9. Экзаменационная сессия студентов-заочников по специальным дисциплинам характеризуется следующими данными:
10. Оценка студентами профессиональных качеств преподавателей представлена в следующей таблице:
Рассчитайте коэффициент взаимной сопряженности К. Пирсона. . ПЕРЕЧЕНЬ ВОПРОСОВ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
1. Предмет статистической науки, основные задачи. 2. Возникновение и понятие статистики как науки. 3. Предмет статистического анализа и его основные черты. 4. Роль статистики в анализе социально-экономических явлений. Статистическая методология. 5. Основные принципы организации и задачи статистики в РФ. 6. Основные формы статистической отчетности и методы обработки первичной информации в РФ. 7. Понятие и основные этапы статистического исследования. 8. Статистическое наблюдение. Организационные формы статистического наблюдения. 9. План статистического наблюдения, его составные части. 10. Виды статистического наблюдения. 11. Ошибки статистического наблюдения и методы их контроля. 12. Проблемы организации статистического наблюдения. 13. Задачи и основные содержание сводки статистических данных. 14. Группировка как основа научной обработки статистических данных. Виды группировок. 15. Задачи группировок и их значение в статистическом исследовании. 16. Проблема выбора группировочных признаков, определение числа групп и величины интервалов. 17. Статистические таблицы, их элементы и виды. 18. Правила построения статистических таблиц. 19. Ряды распределения, их виды и характеристики. 20. Графический метод в статистике. Виды графиков и принципы их построения. 21. Абсолютные статистические величины и их виды. 22. Относительные статистические величины и их виды. Связь между абсолютными и относительными величинами. 23. Средине величины в статистике, их сущность и определение. 24. Степенные средние, их виды. Общая формула средней степенной. Правило мажорантности средних. 25. Средняя арифметическая величина. Вычисление средней арифметической, сфера применения. 26. Средняя гармоническая величина, ее вычисление, сфера применения. 27. Средняя геометрическая величина, ее вычисление, сфера применения. 28. Структурные средние и их виды. 29. Мода, ее вычисление, сфера применения. 30. Медиана, ее вычисление, сфера применения. 31. Квартили, децили, перцентили, их вычисление, сфера применения. 32. Понятие вариации. Показатели вариации, их классификация и роль в статистическом анализе. 33. Абсолютные показатели вариации, способы их вычисления. 34. Относительные показатели вариации способы их вычисления. 35. Дисперсия альтернативного признака. 36. Правило сложения дисперсий. 37. Индексы, их виды и роль в анализе сложных социально-экономических явлений. 38. Индивидуальные и общие индексы. Агрегатный индекс как основная форма общего индекса. 39. Средний арифметический и средний гармонический индексы. 40. Ряды цепных и базисных индексов с постоянной и переменной базой. 41. Общие принципы построения индексов: цен, физического объема продукции, товарооборота, себестоимости и производительности труда. 42. Индексный метод выявления роли отдельных факторов. 43. Ряды динамики, их элементы и виды. 44. Показатели ряда динамики. 45. Методы преобразования рядов динамики. 46. Выявление и характеристика основной тенденции развития при помощи скользящей средней. 47. Выявление и характеристика основной тенденции развития при помощи метода аналитического выравнивания. 48. Изучение и измерение сезонных колебаний. 49. Интерполяция и экстраполяция рядов динамики. 50. Понятие о статистической и корреляционной связи. 51. Задачи корреляционно-регрессионного анализа и моделирования. 52. Условия применения и ограничения корреляционно-регрессионного метода. 53. Коэффициент корреляции рангов. 54. Понятие о стохастических и функциональных связях. 55. Сущность линии регрессии и основные модели корреляционной связи. 56. Регрессионные модели: этапы построения и анализа. 57. Применение корреляционно-регрессионных моделей в анализе и прогнозе. 58. Метод аналитических группировок. 59. Оценка тесноты связи. 60. Измерение тесноты связи между явлениями. Коэффициенты детерминации.
ЛИТЕРАТУРА
1. Статистика: Учебник/Под ред. И.И. Елисеевой. – М.: Высшее образование, 2009. 2. Статистика: Учебник/Под ред. В.С. Мхитаряна. – М. Экономистъ, 2009. 3. Теория статистики: Учебник/Р.А. Шмойлова. – М.: Финансы и статистика, 2008. 4. Ниворожкина Л.И., Чернова Т.В. Теория статистики (с задачами и примерами по региональной экономике).- Ростов н/Д: «Мини Тайп», «Феникс», 2005. 5. Ниворожкина Л.И., Рудяга А.А., Федосова О.Н. Теория статистики: Справочные материалы, контрольные вопросы и задания. Учебно-метод. пособие/ Рост. гос. эконом. универ. «РИНХ» – Ростов-н/Д., 2005. – 186 с. 6. Курс социально-экономической статистики: Учебник для вузов /Под ред. проф. М.Г. Назарова. – М.: Финстатинформ, 2002. 7. Громыко Г.Л. Общая теория статистики: Учебник. – М.: Финансы и статистика, 2001. 8. Гусаров В.М. Статистика: Учебное пособие для вузов – М.: ИНФРА-М, 1999. 9. Елисеева И.И., Юзбашев В.М. Общая теория статистики: Учебник. – М.: ЮНИТИ-ДАНА, 2001. 10. Ефимова М.Р., Рябцев В.М. Общая теория статистики: – М.: Финансы и статистика, 1991. 11. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: – М.: Финансы и статистика, Инфра-М, 2001. 12. Кожухарь Л.И. Основы общей теории статистки. – М.: Финансы и статистика, 1999. 13. Общая теория статистики. Статистическая методология в изучении коммерческой деятельности/Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2001. 14. Октябрьский П.Л. Статистика: Учебное пособие. – СПб.: 2001. 15. Практикум по статистике: Учебное пособие/Под ред. проф. В.М. Симчеры. – М.: ЗАО «Финстатинформ», 1999. 16. Практикум по теории статистики: Учебное пособие/Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2008. 17. Статистика: Учебное пособие (серия «Вопрос-ответ»)/Под ред. проф. М.Р. Ефимовой. – М.: ИНФРА-М, 2000. 18. Теория статистики: Учебник/Под ред. проф. Г.Л. Громыко. – М.: ИНФРА-М, 2000. 19. Экономическая статистика. Учебник./Под ред. Ю.Н. Иванова. М.: ИНФРА-М, 1998.
[1] Медиана обладает свойством: сумма абсолютных величин отклонений вариантов от медианы меньше, чем от любой другой величины, т.е. åïхi - Меï = min. [2] Квантили не всегда совпадают с определенными вариантами. Квантиль – это либо вариант ряда, либо промежуточное значение между двумя соседними вариантами. [3] Использование коэффициента вариации имеет смысл при изучении вариации признака, принимающего только положительные значения. Совершенно неправильно пользоваться V в случае измерения колеблемости признака, принимающего как положительные, так и отрицательные значения. Не имеет смысла, например, V, вычисленный для изучения колеблемости среднегодовой температуры воздуха, что особенно ясно при среднегодовой температуре близкой к нулю. [4] Существует много других аналитических выражений коэффициента Джини, но в целях экономии места мы остановимся на одном.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.122.145 (0.013 с.) |






 , (8.1)
, (8.1)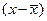 и
и 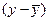 ;
;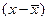 и
и 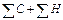 – общее количество парных отклонений.
– общее количество парных отклонений.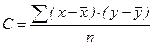 (8.2)
(8.2)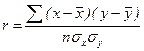 (8.3)
(8.3)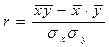 , (8.4)
, (8.4)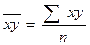
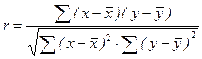 (8.5)
(8.5)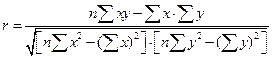 (8.6)
(8.6)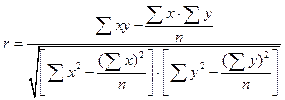 (8.7)
(8.7)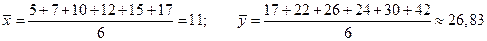 .
.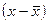
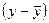
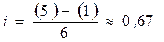
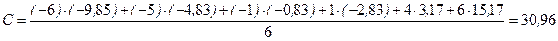
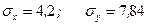 ,
, 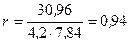
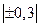
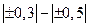
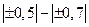
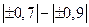
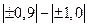

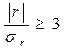
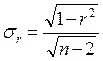
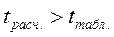 , где
, где 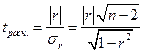
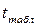 находится по таблице распределения Стьюдента с параметрами
находится по таблице распределения Стьюдента с параметрами 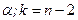
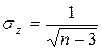
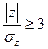 , где
, где 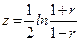 z – преобразование Фишера
z – преобразование Фишера
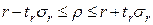 , (8.8)
, (8.8)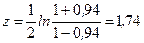 ,
, 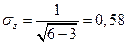 , тогда
, тогда 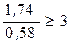 , что указывает на значимость коэффициента корреляции.
, что указывает на значимость коэффициента корреляции.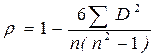 (8.9)
(8.9)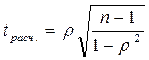 (8.10)
(8.10) , где
, где 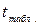 находится по таблице распределения Стьюдента с параметрами
находится по таблице распределения Стьюдента с параметрами 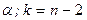 .
.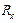
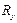
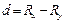
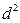
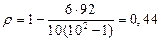 .
.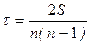 , (8.11)
, (8.11)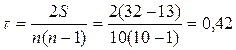
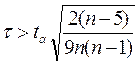 , (8.12)
, (8.12)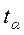 - коэффициент, определяемый по таблице нормальгого распределения для выбранного уровня значимости
- коэффициент, определяемый по таблице нормальгого распределения для выбранного уровня значимости 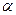 при больших п.
при больших п.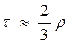 . Это соотношение выполняется при большом числе наблюдений, т.е п>30, и слабых либо умеренно тесных связях.
. Это соотношение выполняется при большом числе наблюдений, т.е п>30, и слабых либо умеренно тесных связях.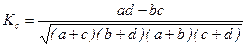 (8.13)
(8.13)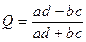 (8.14)
(8.14)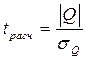 , где (8.15)
, где (8.15)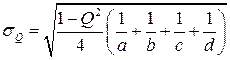 (8.16)
(8.16)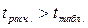 , где
, где 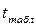 находится по таблице функции Лапласа при уровне значимости ά (обычно берется на уровне 5%).
находится по таблице функции Лапласа при уровне значимости ά (обычно берется на уровне 5%).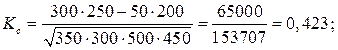
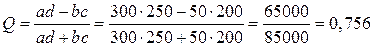 .
.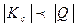 .
.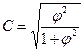 (8.17)
(8.17)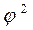 - показатель средней квадратической сопряженности, рассчитываемый как
- показатель средней квадратической сопряженности, рассчитываемый как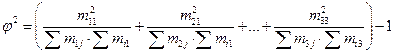 (8.18)
(8.18)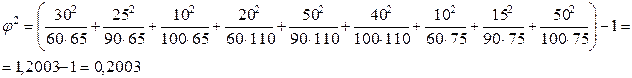
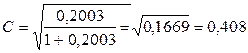 .
. (8.19)
(8.19)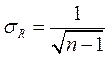 (8.20)
(8.20)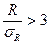 , то с вероятностью близкой к 0,99 можно считать коэффициент множественной корреляции значимым.
, то с вероятностью близкой к 0,99 можно считать коэффициент множественной корреляции значимым.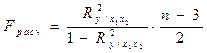 (8.21)
(8.21)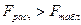 , где
, где 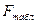 находится по таблице распределения Фишера с параметрами (а; 2; n – 3).
находится по таблице распределения Фишера с параметрами (а; 2; n – 3).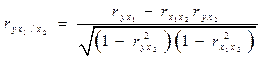 (8.22)
(8.22)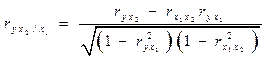 (8.23)
(8.23)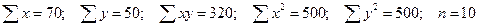 .
.


