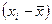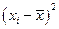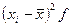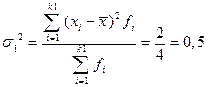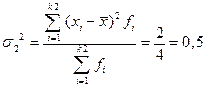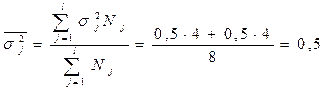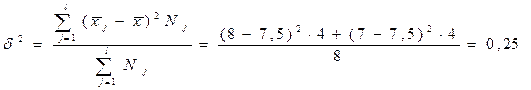Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Справочные материалы (Средние величины)Содержание книги Поиск на нашем сайте
Наиболее распространенными статистическими показателями являются статистические показатели в форме средних величин. Средняя величина – это обобщающая мера варьирующего признака, характеризующая его уровень в расчете на единицу совокупности. Условиями применения средних величин являются: наличие качественно однородной совокупности и достаточно большой ее объем. Определить среднюю во многих случаях можно через исходное соотношение средней или её логическую формулу:
Числитель исходного соотношения средней представляет собой определяющий показатель. Различают две основных формы средних: Степенные средние Структурные средние
Общая формула степенной средней простой записывается следующим образом:
Общая формула степенной средней взвешенной записывается следующим образом:
Изменение показателя степени k приводит в каждом отдельном случае к определенному виду средней:
Степенные средние, исчисленные для одной и той же совокупности, имеют различные количественные значения. Это отражено в правиле мажорантности средних:
Пример 4.11. Рассмотрим следующие данные о реализации продукта одного вида на трех рынках:
Требуется рассчитать среднюю цену, по которой продавался товар. Исходное соотношение средней или ее логическая формула выглядит следующим образом:
Пусть, мы располагаем только данными о ценах на трех рынках и о количестве товара, проданного на каждом их них. При этом цены на отдельных рынках выступают в качестве вариантов, а количество проданного товара – в качестве весов. Тогда средняя цена определится по средней арифметической взвешенной, то есть
Теперь предположим, что количество проданного товара неизвестно, а известны цены и выручка от продажи. В этом случае расчет следует записать в форме средней гармонической взвешенной, т.е.
Результат, как и следовало ожидать получился тот же. Пример 4.12. Предположим, что произведены инвестиции, приносящие ежегодный доход. Процент доходности меняется из года в год. Например, в течение 5 лет получен % дохода i1 - в первый год, i2 - во второй год, i3 - в третий год, i4 - в четвертый год, i5 - в пятый год. Доход на инвестиции начисляется один раз в год. Это значит, что после первого года сумма, равная процентному приросту i1, добавляется к первоначальной сумме счета. Если необходимо найти средний уровень дохода за пять лет, то можно сложить i1, i2, i3, i4, i5 и разделить на 5. Полученная величина будет арифметической средней уровня дохода за 5 лет. С другой стороны, если первоначальная сумма инвестиций - Р, то после первого года мы имеем Р(1+i1). В конце второго года эта сумма составит Р.(1+i1)(1+i2) и т.д. После истечения пяти лет получим: F=Р.(1+i1)(1+i2)(1+i3)(1+i4)(1+i5). Если необходимо определить средний процент дохода i, который даст сумму дохода F по истечении пяти лет, при прибавлении ежегодного накопленного прироста к сумме вклада, то это должна быть геометрическая средняя процента по вкладу. Уровень процента i есть средняя из i1, i2, i3, i4,i5 в мультипликативном смысле. Это коэффициент, который находится из следующего уравнения: (i+1)5=(1+i1).(1+i2).(1+i3).(1+i4).(1+i5). Решение этого уравнения находится по формуле:
где (i+1) - геометрическая средняя из (1+i1),(1+i2),(1+i3),(1+i4),(1+i5). Например, предположим, что n = 2 года, i1 = 0,10 и i2 = 0,05. Геометрическая средняя от (1+i1) и (1+i2) есть:
Эта средняя дает процентный рост по вкладу за два года - 0.0747 или 7,47%. Если использовать среднюю арифметическую, то x = (0,10+0,05)/2 = 0,075, что несколько отличается от геометрической средней. Разница в данном примере невелика, но расчет по формуле средней геометрической более верен. Пример 4.13. Максимальный выигрыш в лотерее равен 1000000 рублей, а минимальный – 100 рублей. Какую величину можно считать средней между миллионом и сотней? Арифметическая средняя, равная 500050 руб., здесь непригодна, т.к. это, как и миллион, крупный, а никак не средний выигрыш. Геометрическая средняя в этом случае дает наиболее правильный с точки зрения экономики и логики ответ:
При изучении статистической совокупности применяются такие ее характеристики, которые описывают количественно ее структуру, строение. Квантили – это варианты, занимающие определенное место в ранжированной совокупности. К числу квантилей, наиболее часто используемых в статистическом анализе, относят перцентили, квартили, децили и медиану, которые характеризуют структуру совокупности. Перцентиль – это значение признака в определенной позиции ранжированного ряда, мера относительной позиции варианта в ряду. Р-тый перцентиль – это значение признака, слева от которого лежит Р% вариантов ряда. Позиция Р-го перцентиля задается как (n+1)Р/100, где n-число вариантов ряда. В статистике наиболее часто применяются квантили, которые делят ряд на четыре равные части – квартили (от латинского слова quarta - четверть). Первый квартиль (25-й перцентиль) – это значение признака, слева от которого лежит 1/4 (или 25%) всех вариантов. Второй квартиль – это 50 перцентиль или медиана. Медиана – значение признака, относительно которого совокупность делится на две равные по числу вариантов части.[1] Третий квартиль - это точка, слева от которой находится 3/4 или 75% вариантов ряда. 25-й перцентиль называют – нижним квартилем (Q1,), 50-й перцентиль (медиану) – средним квартилем (Q2), 75-й перцентиль – верхним квартилем (Q3). В статистическом анализе также часто применяют квантили, которые делят совокупность на десять равных частей – децили. Их значения определяются соответственно как 10, 20,..., 90 перцентили. В общем случае квантили интервального вариационного ряда определяются по формуле:
где хQp(min) – нижняя граница интервала, в котором находится квантиль; k – величина квантильного интервала (интервальная разность); VQp-1 – накопленная частота или частость интервала, предшествующего квантильному; Р – доля признаков, находящихся левее квантиля (например, для верхнего квартиля -0,25, для медианы -0,5, для седьмого дециля - 0,7); Σfi – сумма всех частот; fQp – частота квантильного интервала.
Для расчета значения медианы в интервальном вариационном ряду вначале находят интервал, содержащий медиану. Медианному интервалу соответствует первая из накопленных частот или частостей, превышающая половину всего объема совокупности. Внутри медианного интервала расчет значения медианы производится по формуле:
где k – величина медианного интервала;
Мода – это значение признака, наиболее часто встречающееся в совокупности. В интервальном вариационном ряду мода рассчитывается по следующей формуле:
где k – величина модального интервала;
Пример 4.14. Правительство развивающейся страны объявило конкурс для зарубежных инвесторов на заключение контракта по строительству нового морского порта. В ответ были получены следующие предложения цены (млрд. долл.): 2, 3, 2, 4, 3, 5, 1, 1, 6, 4, 7, 2, 5, 1, 6. Построить вариационный ряд, найти среднюю арифметическую, квартили и 65-ый перцентиль.
Решение: Строим вариационный ряд
Рассчитаем среднюю арифметическую взвешенную:
Определим первый квартиль или 25-ый перцентиль. Позиция этого перцентиля: (15+1)*0,25=4. Четвертое по порядку значение равно 2, т.е. Q1=2. Определим второй квартиль или 50-ый перцентиль, т.е. медиану. Позиция этого перцентиля: (15+1)*0,5=8. Восьмое по порядку значение равно 3, т.е. Q2=Ме=3. Определим третий квартиль или 75-ый перцентиль. Позиция этого перцентиля: (15+1)*0,75=12. Двенадцатое значение признака равно 5, т.е. Q3=5. Позиция 65-го перцентиля: (15+1)*0,65=10,4. Десятый по порядку вариант равен 4, а одиннадцатый равен 5. Значение 65-го перцентиля находится в точке, которая делит расстояние десятым и одиннадцатым признаком в отношении 0,4 к 1. Следовательно, Р65=4+0,4(5-4)=4,4.[2] Среднюю арифметическую, медиану и моду часто называют мерами центральной тенденции. Что характеризуют эти три меры и каковы их достоинства и недостатки? Средняя суммирует всю информацию и является центром массы. Медиана – это значение признака в центре набора данных. Одна половина значений признака лежит левее этой точки, другая – правее. Точное местонахождение любой точки не существенно при определении медианы; важно только ее положение относительно центрального значения, т.е. медиана устойчива по отношению к крайним значениям ряда. Средняя арифметическая напротив чувствительна к положению крайних значений ряда. Тем не менее, средняя арифметическая имеет существенные преимущества перед другими мерами центральной тенденции. Средняя арифметическая основывается на информации, содержащей все значения ряда, в то время как медиана базируется только на значении, лежащем «в середине ряда». Если же необходимо предотвратить влияние нескольких наблюдений, лежащих далеко от центра ряда, то надо использовать и медиану. Например, если изучается распределение доходов и имеет место высокая степень неравенства, т.е. присутствует некоторое число единиц наблюдения как с очень высокими, так и с очень низкими доходами, то логичнее рассчитывать не средний доход, а медианный. В такой ситуации он более адекватно отразит типичное значение дохода. Мода не так популярна в статистическом анализе как средняя арифметическая и медиана. В одном ряду может быть несколько мод. Моде отдается предпочтение при изучении цен на рынке, спроса населения на отдельные продукты питания, одежду и обувь определенных размеров. Если средняя арифметическая близка к моде и медиане, то она типична. Вычисление моды особенно существенно в несимметричных рядах, когда она сильно отличается от медианы и средней арифметической.
4.6. Домашнее задание к теме 4 1. Имеются следующие данные о численности экономически активного населения России по состоянию на начало 2001 г. (в млн. чел.):
Исчислить, сколько безработных приходится на 1000 занятых в экономике России
2. Имеются следующие данные о розничном товарообороте Российской Федерации за 2001 – 2002 гг. (в млрд. руб.):
Вычислите относительные показатели структуры розничного товарооборота и показатели координации. Сделайте сравнительный анализ изменения структуры.
3. По данным о пассажирообороте всех видов транспорта (в млрд. пассажиров) вычислите относительные показатели структуры пассажирооборота за 1995 и 2000 гг.:
Результаты представьте в виде таблицы и проанализируйте полученные данные.
4. По данным нижеследующей таблицы определите отдельно для мужчин и женщин относительные показатели, характеризующие: а) долю безработных, получающих пособие по безработице; б) долю безработных, проходящих профессиональное переобучение.
Проведите сравнительный анализ рассчитанных долей. Определите долю женщин среди безработных, получающих пособие, и среди безработных, проходящих профессиональное переобучение. Сделайте выводы.
5. На основе данных о распределении населения региона по возрасту и виду поселения определите относительные показатели, характеризующие: а) структуру городского и сельского населения по признаку трудоспособности, проведите сравнительный анализ структур; б) соотношение населения трудоспособного и нетрудоспособного возраста в городах и селах; в) структуру населения по виду поколений; г) соотношение городского и сельского населения.
Среднегодовая численность населения Российской Федерации в 1999 г. составила 148,6 млн. чел., число родившихся – 1796,6 тыс. чел., число умерших – 1690,7 тыс. чел.; в 2002 г. – соответственно 147,7 млн., 1304,6 тыс., 2082,2 тыс. чел. Определите показатели интенсивности естественного движения населения Российской Федерации за 1999 и 2002 гг.
6. Имеются данные о розничном товарообороте области за 2000 г. (в млрд. руб.):
Определите показатели структуры розничного товарооборота по формам собственности и показатели координации. 7. Имеются следующие данные о внешнеторговом обороте со странами дальнего зарубежья и СНГ, млн. долл.:
Вычислите относительные показатели структуры и координации.
8. Численность врачей в РФ характеризуется следующими данными (на начало года, тыс. чел.):
Проведите анализ изменения обеспеченности населения врачами, если известно, что численность постоянного населения на начало 1981 г. составляла 139,0 млн. чел., в т.ч. в возрасте до 14 лет – 30,1 млн. чел., а на начало 1995 г. – соответственно 147,9 и 31,8 млн. чел.
9. Имеются следующие данные об объемах производства продукции черной металлургии в РФ, тыс.т:
Охарактеризуйте уровень экономического развития с учетом численности населения РФ, которая составляла на начало года, млн. чел.: в 1993 г. – 148,7; в 1994 г. – 148,3 и в 1996 г. – 148,2.
10. По региону имеются следующие данные о вводе в эксплуатацию жилой площади:
Определить: 1) динамику ввода в эксплуатацию жилой площади по каждому виду жилых домов и в целом по региону; 2) структуру введенной в эксплуатацию жилой площади в прошлом и отчетном годах. 11. Просроченная задолженность по кредитам акционерным обществ (АО) за отчетным период характеризуется следующими данными:
Определить средний процент просроченной задолженности акционерного общества.
12. Доходы банков в отчетном году характеризуется следующими показателями:
Определить среднюю процентную ставку.
13. Результаты работы страховых организаций в Ι полугодии характеризуется следующими данными:
Определить: 1) средний коэффициент выплат; 2) абсолютную сумму дохода страховых операций; 3) относительную доходность. 14. Рентабельность активов акционерного общества характеризуется следующими данными:
Определить рентабельность активов по АО в целом.
15. За первый год производительность труда выросла на 10%, за второй упала на 5%, а за третий выросла на 4%. Чему равен среднегодовой прирост производительности труда? 16. Имеются данные об итогах торгов на российских валютных биржах за 6.02.1995 г.
Вычислите средний курс доллара по результатам биржевых торгов?
17. Продукция, производимая малым предприятием, имеет разный уровень рентабельности реализации. В декабре этот показатель составил:
Определите средний уровень рентабельности реализации продукции. Обоснуйте выбор средней.
18. Финансирование инвестиций в основные средства за счет собственных средств по предприятиям акционерного общества за отчетный период характеризуется следующими данными:
Необходимо определить средний удельный вес собственных средств в общем объеме инвестиций в основные средства по АО.
19. В будние дни на протяжении торговой недели цена изделия оставалась на уровне 246 руб. «Распродажная» цена в субботу и в воскресенье была ниже на 20%. Определить среднюю цену изделия за неделю.
20. Имеются данные о финансовых показателях фирм, тыс. руб.:
Определите средний процент рентабельности акционерного капитала фирм, используя показатели: а) гр.1 и 2; б) гр. 2 и 3; в) гр. 1 и 3; г) гр. 3 и 4.
21. Имеются следующие данные об оплате труда работников малых предприятий:
Определите среднюю заработную плату работников предприятий, используя показатели: а) гр. 1 и 2; б) гр. 2 и 3; в) гр. 1 и 3; г) гр. 3 и 4.
22. Банк имеет данные о работе трех обменных пунктов валюты за день:
Определите средний взвешенный курс доллара по трем обменным пунктам банка, используя показатели: а) гр. 1 и 2; б) гр. 1 и 3; в) гр. 2 и 3.
23. Выработка тканей по цехам фабрики характеризуется следующими показателями:
Вычислите выработку ткани на одного рабочего в среднем по фабрике за март и за апрель. В каком месяце и на сколько средняя выработка выше? Укажите, какие виды средних применяли.
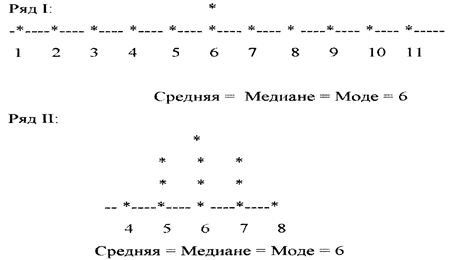
24. Следующие данные представляют число пассажиров компании «Аэрофлот-Дон» на рейсах Ростов – Москва за январь месяц: 133, 114, 119, 120, 127, 125, 123, 109, 116, 121, 123, 128, 131, 136, 132, 110, 118 121, 128, 123, 130, 129, 128, 132, 136, 134, 129, 134, 128, 136, 134. Чему равно среднее число пассажиров на рейсах? Найдите квартили, 10, 15 и 65 перцентили. Тема 5. Измерение вариации Справочные материалы Пример 5.1. Рассмотрим два вариационных ряда: Ряд I: 1, 2, 3, 4, 5, 6, 6, 7, 8, 9, 10, 11. Ряд II: 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8. В чем отличие между рядами, если
Рис.6.1. Сравнение вариации рядов I и II Рисунок 6.1. графически изображает ряд I и ряд II. Ряд I более вариабелен, чем ряд II. В статистике используется ряд мер вариабельности (колеблемости). Интерквартильный размах определяют как разницу между третьим и первым квартилями.
Другая подобная мера – размах вариации – разность между наибольшим и наименьшим значениями признака ряда.
По данным примера 5.1 имеем IQRI = 5,5; IQRII = 2; RI = 10; RII = 4.
Существуют и другие более часто используемые меры вариации. Это: среднее линейное отклонение, дисперсия и стандартное отклонение (или среднее квадратическое отклонение), определяющие вариацию как меру отклонений значений признаков вариационного ряда от центра ряда распределения – средней арифметической. Среднее линейное отклонение есть средняя арифметическая абсолютных значений отклонений значений признаков ряда от их средней арифметической. - простое:
- взвешенное:
Дисперсия вариационного ряда есть средняя арифметическая квадрата отклонения (средний квадрат отклонения) значений признаков ряда от их средней арифметической. - простая:
- взвешенная:
Стандартное (среднее квадратическое) отклонение вариационного ряда есть арифметическое значение корня квадратного из дисперсии.
- простое:
- взвешенное:
Для ручного счета лучше пользоваться формулой дисперсии следующего вида.
Для оценки интенсивности вариации и сравнения ее в разных совокупностях и различных признаков применяются относительные показатели вариации, которые вычисляются как отношение абсолютных показателей силы вариации к средней арифметической. Существуют следующие показатели, выраженные в процентах: относительный размах вариации, относительное линейное отклонение и коэффициент вариации. Относительный размах вариации (коэффициент осцилляции) отражает относительную меру колеблемости крайних значений признака вокруг средней.
Относительное линейное отклонение отражает долю усредненного значения абсолютных отклонений от средней величины.
Коэффициент вариации позволяет представить дисперсию как долю от средней величины.
Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее средняя.[3] Для более ясного представления и использования в экономико-статистическом анализе показатели вариации представлены на схеме 6.1. При изучении вариации для сгруппированных данных выделяют три вида дисперсий: общую дисперсию, внутригрупповую (частную) дисперсию, межгрупповую дисперсию. Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов.
Схема 5.1. Статистическое изучение вариации
Внутригрупповая (частная) дисперсия измеряет вариацию признака внутри группы.
где xi – значения признаков внутри j-й группы;
fi – частоты вариантов в j-й группе;
Средняя из внутригрупповых (частных) дисперсий.
где Nj – объем j-й группы, j=1,2,…, l (l – число групп),
Межгрупповая дисперсия измеряет колеблемость групповых средних вокруг общей средней и отражает вариацию, обусловленную признаком, положенным в основу группировки.
где
Существует закон (правило сложения дисперсий), связывающий три вида дисперсии. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий.
Зная любые два вида дисперсий, всегда можно найти или проверить правильность расчета третьего вида.
Правило сложения дисперсий позволяет оценить степень влияния группировочного признака на результативный признак и количественно измерить степень этого влияния. Для этого применяется коэффициент детерминации, который показывает степень колеблемости в процентах результативного признака в зависимости от степени колеблемости факторного и рассчитывается как отношение факторной дисперсии к общей дисперсии результативного признака.
Корень квадратный из коэффициента детерминации называют эмпирическим корреляционным отношением (ЭКО), которое показывает степень тесноты связи.
Это показатель принимает значения в интервале [0,1]. Если связь отсутствует, то h=0. В этом случае дисперсия групповых средних равна нулю (
Пример 5.2. Опрос 8 биржевых брокеров дал следующие результаты:
Среднее число контрактов, заключенных брокерами:
В данном примере переподготовка – факторный признак, а число заключаемых контрактов – результативный. Сгруппируем эти данные по признаку переобучения и рассчитаем средние по каждой группе.
Или по формуле для взвешенных вариант
Или по формуле для взвешенных вариант
Рассчитаем дисперсии в каждой группе. Дисперсия числа заключенных контрактов у брокеров, прошедших переобучение:
Дисперсия числа заключенных контрактов у брокеров, не прошедших переобучение:
Рассчитаем среднюю из внутригрупповых дисперсий:
Этот показатель характеризует влияние на результативный признак всех прочих факторных признаков за исключением признака, положенного в основу группировки. Очевидно, что различие в числе заключенных контрактов в двух группах вызвано тем, что брокеры первой группы прошли переобучение, а брокеры второй группы не прошли. Найдем дисперсию между группами (межгрупповую дисперсию).
Этот показатель характеризует влияние на результативный признак факторного признака, положенного в основу группировки. Рассчитаем общую дисперсию числа заключенных контрактов.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

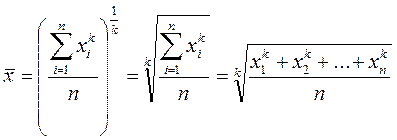
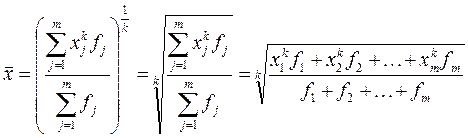
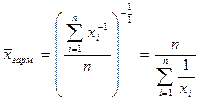
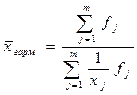
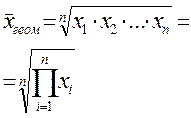
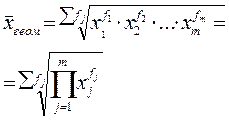
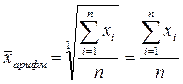
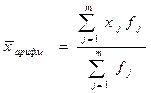
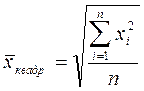
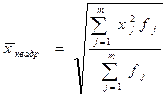

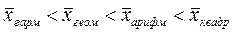
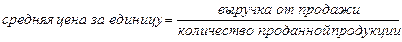
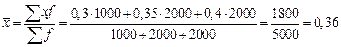 .
.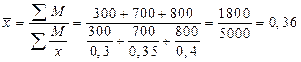 .
.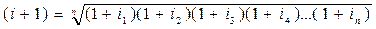
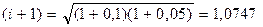
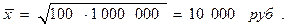
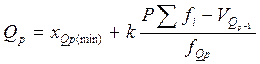 ,
,
 ,
,
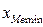 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;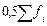 - половина суммы всех частот (или частостей);
- половина суммы всех частот (или частостей);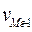 - накопленная частота или частость интервала, предшествующего медианному;
- накопленная частота или частость интервала, предшествующего медианному;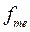 - частота медианного интервала.
- частота медианного интервала.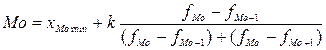 ,
,
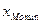 - нижняя граница модального интервала;
- нижняя граница модального интервала;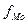 - частота модального интервала;
- частота модального интервала;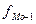 - частота интервала предшествующего модальному;
- частота интервала предшествующего модальному;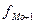 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.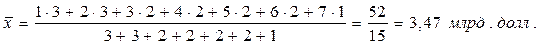
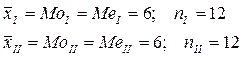
 (5.1)
(5.1)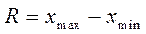 (6.2)
(6.2)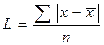 (5.3)
(5.3)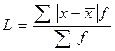 (5.4)
(5.4)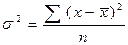 (5.5)
(5.5)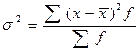 (5.6)
(5.6)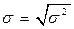 5.7)
5.7)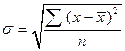 (5.7а)
(5.7а)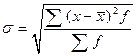 (5.7б)
(5.7б)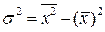 (5.8)
(5.8)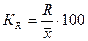 (5.9)
(5.9)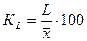 (5.10)
(5.10)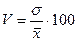 (5.11)
(5.11)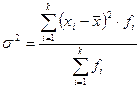 (5.12)
(5.12)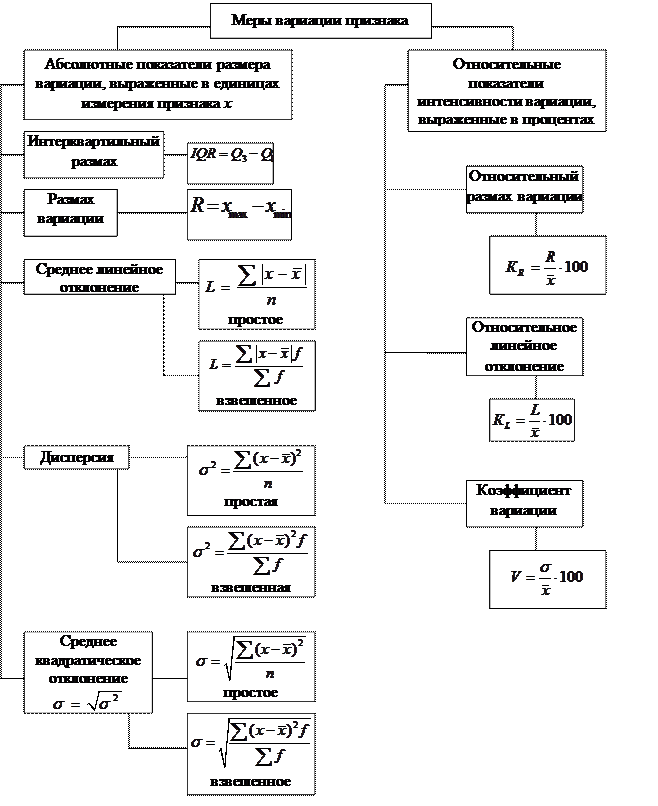
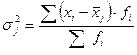 (5.13)
(5.13)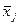 – средняя арифметическая j-й группы;
– средняя арифметическая j-й группы;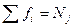 – объем j-й группы. Суммирование и в числителе, и в знаменателе осуществляется только по тем признакам, которые попали в j-ю группу.
– объем j-й группы. Суммирование и в числителе, и в знаменателе осуществляется только по тем признакам, которые попали в j-ю группу.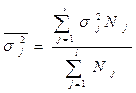 (5.14)
(5.14)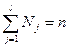 - общее число признаков ряда.
- общее число признаков ряда.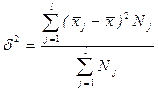 (5.15)
(5.15)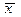 - общая средняя вариационного ряда.
- общая средняя вариационного ряда.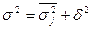 (5.16)
(5.16)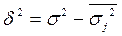 (5.16а)
(5.16а)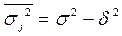 (5.16б)
(5.16б)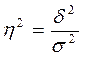 (5.17)
(5.17)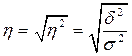 (5.18)
(5.18)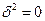 ), то есть все групповые средние равны между собой и межгрупповой вариации нет. Если связь функциональная, то h=1. В этом случае дисперсия групповых средних равна общей дисперсии (
), то есть все групповые средние равны между собой и межгрупповой вариации нет. Если связь функциональная, то h=1. В этом случае дисперсия групповых средних равна общей дисперсии (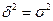 ). Промежуточные значения h оцениваются по степени их близости к предельным.
). Промежуточные значения h оцениваются по степени их близости к предельным.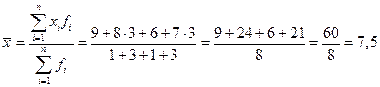 .
.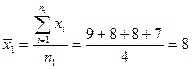 , где n1 – число признаков в первой группе.
, где n1 – число признаков в первой группе.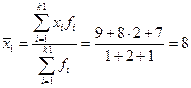 , где fi – частоты ряда.
, где fi – частоты ряда.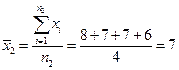 , где n2 – число признаков во второй группе.
, где n2 – число признаков во второй группе.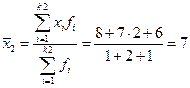 , где fi – частоты ряда.
, где fi – частоты ряда.