
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Статистическое наблюдениеСодержание книги Поиск на нашем сайте
ОГЛАВЛЕНИЕ Методические указания к темам курса.. 4 Тема 1. Статистическое наблюдение. 4 Тема 2. Сводка и группировка статистических материалов. Статистические таблицы 4 Тема 3. Абсолютные и относительные величины.. 5 Тема 4. Средние величины.. 6 Тема 5. Распределение признака в совокупности. 8 Тема 6. Ряды динамики. 9 Тема 7. Индексы.. 11 Тема 8. Выборочное наблюдение. 14 Тема 9. Методы статистического изучения взаимосвязи. 16 Контрольные задания.. 17 Сводка и группировка статистических материалов. 18 Относительные величины.. 22 Средние величины и показатели вариации. 24 Ряды динамики. 28 Индексы.. 30 Методы статистического изучения взаимосвязей. 33 Выборочные наблюдения. 35 Библиографический список.. 38
Тема 1. Статистическое наблюдение Изучив тему, студент должен уяснить значение статистического наблюдения как первого этапа статистического исследования иисточника всех статистических данных. Знать, что от качества выполнения статистического наблюдения зависят качество результатов последующих этапов исследования и конечные выводы. Уяснив основные понятия статистического наблюдения, можно переходить к изучению вопроса о видах статистического наблюдения, формах организации собирания статистических сведений и способах получения сведений в результате применения каждой формы статистического наблюдения. Особое внимание должно быть уделено вопросам организации статистического учета и отчетности. Надо усвоить принципы организации отчетности; иметь четкое представление об отчетной единице, видах первичного учета и взаимосвязи первичного учета и отчетности. Заключительными вопросами темы являются вопросы о неточности данных (ошибках) наблюдения и мерах по их устранению, а также контроле собранных данных статистического наблюдения. Тема 2. Сводка и группировка статистических материалов. Тема включает вопросы о содержании сводки и группировках, об их задачах и значении, о видах и принципах группировок; о статистических таблицах как форме изложения результатов сводки; об организации и технике сводки. Группировка, сводка и составление статистических таблиц являются связанными элементами в работе по обобщению и систематизации данных статистического наблюдения. В статистике группировки широко применяются для анализа производственной деятельности предприятий и организаций. Студент должен иметь представление об основных группировках – типологических, структурных и аналитических. С важнейшими группировками статистики можно ознакомиться по данным статистического ежегодника Госкомстата России. В результате изучения вопроса о статистических таблицах студенту следует уяснить значение таблицы как основной формы выражения статистического суждения об изучаемом явлении; ознакомиться с элементами таблицы (заголовок, подлежащее, сказуемое), видами статистических таблиц (простые, групповые, комбинационные); ознакомиться с приемами чтения и анализа таблиц; необходимо научиться не только хорошо строить и оформлять таблицу, но и формулировать выводы на основе содержащихся в таблице данных. Тема 3. Абсолютные и относительные величины При статистической сводке данных получают абсолютные величины, которые характеризуют размеры явления. Для того чтобы сделать выводы из данных сводки, необходимо произвести вычисление относительных величин. Относительные величины выражаются в форме коэффициентов, в процентах и промилле. Получают их путем сравнения (деления) абсолютных величин. Различают шесть видов относительных величин. 1. Относительные величины динамики характеризуют изменение уровней одноименных явлений во времени. Основными из относительных величин этого вида являются темпы роста и прироста. Темпы роста получают путем деления уровня какого-либо явления за последующий период на уровень за предшествующий период. Темпы роста выражаются в процентах. Темпы прироста получают путем деления абсолютного прироста уровня явления в последующем периоде на уровень явления в предшествующем периоде. Темпы прироста выражаются так же, как и темпы роста, в процентах. 2. Относительные величины планового задания и выполнения плана Величины выполнения плана характеризуют степень выполнения планового задания и получаются путем деления отчетной абсолютной величины на плановую. Относительные величины планового задания подсчитывают путем деления абсолютной величины планового задания на уровень данного явления, достигнутый в предшествующем (базисном) периоде. Обычно относительные величины планового задания или выполнения плана выражаются в процентах. 3. Относительные величины структуры характеризуют удельные веса составляющих частей целого. 4. Относительные величины интенсивности характеризуют степень распространения или развития данного явления в определенной среде. Они исчисляются как отношение двух разноименных, но взаимосвязанных величин. 5. Относительные величины координации характеризуют отношения отдельных частей совокупности к одной из них, взятой за базу сравнения. Эти величины позволяют контролировать соблюдение необходимых пропорций между отдельными частями целого. 6. Относительные величины сравнения характеризует сравнительные размеры одноименных явлений, относящихся к одному и тому же периоду, но к различным объектам или территориям. Тема 4. Средние величины Изучение темы начинается с вопросов о роли и значении средних величин (далее просто средних) в научном исследовании и об условиях их правильного применения. Правильное применение средних возможно лишь на основе предварительной группировки: выделения качественно однородных совокупностей и расчленения явления на части в зависимости от различия условий, под влиянием которых явление складывается. Под средней величиной в статистике понимают показатель, который характеризует типичный уровень изменяющегося признака в расчете на единицу однородной совокупности в конкретных условиях места и времени. При изучении отдельных видов средних величин рекомендуется четко представлять методику их расчета и область применения. Наиболее распространенной формой средних величин является средняя арифметическая, расчет которой производится путем деления суммы всех значений изучаемого признака на их количество. Формула расчета:
где
Если какое-то значение признака повторяется у нескольких единиц, то в этом случае формула расчета средней арифметической имеет такой вид:
где Расчет средней по формуле (5.1) называется способом простой средней арифметической, а по формуле (5.2) – средней арифметической взвешенной. Средняя хронологическая используется в тех случаях, когда имеются данные наблюдения на определенные моменты времени; ее расчетная формула имеет вид:
Средняя геометрическая используется для анализа темпов роста явлений и вычисляется по следующим формулам:
где
Взвешенные средние широко применяются при обработке данных текущего наблюдения по производственным участкам и цехам предприятия, обобщении материалов отчетности предприятий и организаций. Студент должен хорошо знать способы вычисления этих средних, принципы выбора весов и условия, при которых применяются взвешенная средняя арифметическая или гармоническая. Особого рода средними, используемыми в экономическом анализе для изучения структуры вариационного ряда, являются мода и медиана. Медиана – это значение признака у той единицы совокупности, которая расположена в середине упорядоченного ряда. По данным интервального вариационного ряда, который предварительно ранжирован, медиану определяют по формуле:
где
Если ряд дискретный, то медианой является срединное значение признака, и применение формулы не требуется. Мода – это наиболее часто встречающееся значение признака. В интервальном вариационном ряду ее определяют по формуле:
где
В дискретном ряду мода – это вариант признака, имеющий наибольшую частоту. Тема 6. Ряды динамики Задача темы – изучение методов построения статистических показателей, характеризующих изменение явлений во времени. В процессе изучения темы надо представить сущность рядов динамики и усвоить правила их построения, соблюдение которых обеспечивает сопоставимость статистических рядов динамики и позволяет осуществить их научный анализ. В процессе анализа используются аналитические и обобщающие показатели рядов динамики: уровень ряда, абсолютный прирост, темпы роста и прироста, значение одного процента прироста, коэффициенты опережения и ускорения. Абсолютный прирост: · базисный · цепной Темп роста: · базисный · цепной Темп прироста: · базисный · цепной где
При рассмотрении приемов обработки и анализа данных ряда динамики следует использовать знание принципов взаимосвязи между показателями ряда динамики: · произведение ряда последовательных цепных коэффициентов роста равно соответствующему базисному коэффициенту роста; · частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту; · темп прироста может быть рассчитан путем вычитания ста (процентов) из соответствующего значения показателя темпа роста:
· абсолютное значение 1 %прироста составляет 0,01 предшествующего уровня ряда динамики. Для получения аналитических характеристик ряда динамики исчисляются и средние показатели. Средний уровень периодического ряда динамики и средний абсолютный прирост определяют по формуле средней арифметической. Средний уровень моментного ряда исчисляется по формуле средней хронологической. Средний темп роста определяется по формуле средней геометрической, а средний темп прироста равняется соответствующему среднему темпу роста минус 100:
Особое внимание следует уделить изучению закономерностей изменения ряда в целом: сглаживанию и выравниванию рядов динамики, интерполяции и экстраполяции. Тема 7. Индексы При изучении содержания темы студент должен составить представление об индексе как показателе сравнения двух величин; элементах, входящих в построение индексов; различиях индексов индивидуальных и агрегатных, индексов объемных и качественных показателей. Основное внимание должно быть уделено агрегатным индексам – показателям сравнения характеристик сложных явлений, состоящих из непосредственно не суммируемых элементов. Надо усвоить методику построения агрегатных индексов физического объема продукции. Следует иметь в виду, что основной проблемой при построении этих индексов является проблема выбора показателей-соизмерителей, обеспечивающих сопоставимость числителя и знаменателя индекса. Индексируемые показатели, а также явления, выступающие в роли соизмерителей, могут быть качественными и количественными (объемными). Количественные показатели представляют собой численность тех или иных единиц или общий объем какого-либо признака. Качественные характеризуют уровень явления в расчете на ту или иную единицу совокупности. При построении агрегатных индексов качественных показателей в роли соизмерителей выступают количественные показатели и фиксируются на уровне отчетного периода. При построении агрегатных индексов количественных показателей в роли соизмерителей выступают качественные показатели и фиксируются на уровне базисного периода. Индивидуальные индексы не требуют соизмерителей, т.к. при их расчете сравниваются абсолютно однородные явления:
где q – количество единиц продукции одного вида (шт., т, л,...); p – цена единицы определенного вида продукции (руб.); z – себестоимость единицы определенного вида продукции (руб.); w – производительность труда одного человека (шт., т, л,...). Средние индексы (арифметический, гармонический) студент изучает в связи с агрегатными. Агрегатные индексы качественных показателей применяются в двух формах: в форме индексов переменного состава и в форме индексов фиксированного состава. Индекс среднего уровня может быть представлен как произведение аналитических индексов-сомножителей, каждый из которых отражает изменение только одного фактора, и тем самым – влияние этого изменения на динамику среднего уровня. Первый индекс носит название индекса фиксированного состава, второй – индекса структурных сдвигов.
Например, для анализа динамики среднемесячной производительности труда (w) по группе работников индекс переменного состава определяется по формуле:
(7.3) где
где Индексы, приведенные в формуле (7.4), являются индексами фиксированного состава, т.к. в каждом из них индексируется только одна величина; напротив, индексы, приведенные в формуле (7.3), характеризуют изменение и качественных величин (w), и структуры количественных (T). Эта структура может быть выражена в виде относительных величин:
В дальнейшем, для отражения отличия структуры показателя Т (либо других количественных показателей) в разных условиях, будет применяться обозначение Индексные методы широко применяются для анализа факторов изменения сложных показателей, полученных на основе соизмерения абсолютных величин. В связи с этим необходимо изучить вопрос о способах построения взаимосвязанных индексов и способах расчета абсолютного изменения сложной величины за счет влияющих факторов. Индекс результативного показателя связан с индексами показателей-факторов так же, как абсолютные величины этих показателей:
где
Такая взаимосвязь может быть использована не только для выявления относительного изменения уровня изучаемого явления за счет отдельных факторов, но и для определения размера абсолютного изменения уровня сложного явления в связи с влиянием исследуемых факторов:
Среди наиболее часто используемых в экономических расчетах индексов необходимо отметить: индексы объема
индексы цен
индексы себестоимости
Индексы производительности труда могут иметь три формы: натуральные
стоимостные
трудовые
где t – трудоемкость изготовления единицы продукции. Индексы заработной платы также имеют две формы (индивидуальный индекс и сводный индекс), т.к. заработная плата – это сумма, начисленная в счет оплаты за работу одного человека, т.е. показатель качественный:
где Ф – фонд заработной платы всех работников на исследуемом объекте, f – заработная плата одного работника. В выше приведенных формулах использованы условные обозначения любого учебника «Общей теории статистики». Завершая изучение темы, следует обратить внимание на наличие взаимосвязей между следующими группами индексов: - индивидуальными и сводными; - индексами базисными и цепными; - индексами переменного и фиксированного состава; - индексами взаимосвязанных явлений. Задача 1 Имеются следующие данные о работе промышленных предприятий одной отрасли за год:
Произведите группировку предприятий по стоимости основных средств, образовав следующие группы (в млн руб.): до 500, от 501 до 1000, от 1001 до 1500, от 1501 до 2500, свыше 2500. Для каждой группы подсчитайте: число предприятий, стоимость основных средств, выпуск продукции по плану и фактически в среднем на одно предприятие, а также проценты выполнения плана. Задача 2 По исходным данным к задаче № 1 произведите группировку предприятий по фактическому выпуску продукции, образовав следующие группы (в млн руб.): до 600, от 601 до 1200, от 1201 до 2000, от 2001 до 2800, от 2801 до 3800, свыше 3800. Для каждой группы подсчитайте: число предприятий, стоимость основных средств, выпуск продукции по плану, фактически в среднем на одно предприятие и процент выполнения плана, а также фактическую стоимость выпущенной продукции на один рубль основных средств. Вычислите удельный вес отдельных групп по числу предприятий. Результаты группировки изложите в табличной форме и сделайте краткие выводы, назовите вычисленные в таблице относительные величины. Задача 3 Имеются следующие данные за год по заводам одной промышленной компании:
На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три. Задача 4 На основании данных, приведенных в задаче 3, составьте по группам таблицу зависимости выпуска продукции от величины заводов по размеру основных фондов. Каждая группа должна характеризоваться средним выпуском продукции на один завод, на один миллион рублей основных фондов и на одного рабочего. Задача 5 Требуется произвести разделение предприятий, расположенных в одном из регионов, на две группы: производящие продукцию промышленного назначения и потребительские товары. Внутри каждой группы произвести дополнительную группировку предприятий по уровню динамики (темпам роста) объема производства продукции. Результаты представить в виде комбинационной таблицы и проанализировать.
Задача 6 Имеются следующие данные о выплавке чугуна (в пересчете на передельный):
Произведите группировку доменных печей по полезному объему, образовав следующие группы: до 600 м3, от 601 до 900, от 901 до 1250, свыше 1250 м3. Для каждой группы подсчитайте: число доменных печей, выплавку чугуна, метро-сутки и коэффициент использования полезного объема доменных печей. Подсчитайте удельный вес каждой группы в общей численности печей и общем итоге выплавки чугуна. Какие виды относительных величин подсчитаны? Результаты расчета изложите в табличной форме и сделайте краткие выводы. Примечание: коэффициент использования полезного объема доменных печей по номинальному времени определяется путем деления количества номинальных метро-суток на количество выплавленного чугуна в переводе на передельный. Номинальные метро-сутки (последняя графа условия задачи) получены путем умножения полезного объема доменных печей на календарные сутки октября (31 день). Задача 7 Имеются следующие данные о работе мартеновских печей за I квартал:
Произведите группировку мартеновских печей по выплавке стали, образовав 4-5 групп с равновеликими интервалами. По каждой группе вычислите: число мартеновских печей, выплавку стали, метро-сутки и среднесуточный съем стали с 1 кв. метра площади пода. Примечание. Среднесуточный съем стали с 1 кв. метра площади пода мартеновских печей по фактическому времени определяется путем деления количества выплавленной стали на фактические метро-сутки. Результаты изложите в табличной форме и сделайте краткие выводы. Относительные величины Задача 8 Поставки молока и молочных продуктов в торговую сеть города за отчетный период характеризуются следующими данными:
Определить выполнение плана поставки: 1) по каждому продукту; 2) по всем продуктам в условно-натуральном измерении (в пересчете на молоко). Задача 9 Численность населения и студентов в отдельных странах в первой половине 80-х годов характеризовалась следующими данными:
Определите численность студентов, приходившихся на 10000 человек населения в различных странах. Какую относительную величину вы вычислили? Прокомментируйте полученные результаты. Задача 10 Планом промышленного предприятия предусматривалось снижение затрат на 1 рубль товарной продукции на 4 %, фактически затраты возросли на 2 %. Вычислите относительную величину выполнения плана. Задача 11 Имеются следующие данные о составе и численности промышленно-производственного персонала предприятия по годам:
Определите изменение общей численности всего персонала по годам в процентах (на постоянной и переменной базах сравнения); удельный вес отдельных групп персонала по годам; сколько учеников, специалистов, служащих, руководителей приходится на 1000 рабочих. Объясните, какие виды относительных величин вычислены. Адача 12 Выпуск продукции на заводе в 2002 г. составил 160 млн руб. По плану на 2003 г. предусматривалось выпустить продукции на 168 млн руб., фактически же выпуск составил 171,36 млн руб. Вычислите относительные величины планового задания и выполнения плана. Задача 13 Вычислите относительные величины сравнения по данным о производстве важнейших видов промышленной продукции в отдельных странах:
Задача 14 Производство товарной продукции на заводе в 2002 г. составило 1500 млн руб. По плану на 2003 г. предусматривался прирост объема выпуска продукции на 60 млн руб., фактически же выпуск товарной продукции составил в 2003 г. – 1575,6 млн руб. Вычислите относительные величины планового задания и выполнения плана. Задача 15 Определите установленную среднюю продолжительность трудового дня производственного рабочего по заводу в целом:
Задача 16 Имеются следующие данные о выполнении месячного плана производства продукции металлургическими предприятиями:
Определите по пяти предприятиям средний процент выполнения плана. Задача 17 Вычислите среднемесячный процент брака по заводу за второй квартал по следующим данным:
Задача 18 По четырем заводам промышленной компании имеются следующие отчетные данные за первое полугодие:
Определите план выпуска продукции по каждому заводу на первое полугодие, средний процент выполнения плана за полугодие по промышленной компании в целом, средний процент брака в первом полугодии. Задача 19 Имеются следующие показатели по пяти заводам промышленной компании:
Определите средний процент выполнения плана в каждом квартале и за первое полугодие в целом; средний
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.127.63 (0.01 с.) |

 , (4.1)
, (4.1) – среднее значение изучаемого признака;
– среднее значение изучаемого признака;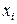 – конкретное значение этого признака;
– конкретное значение этого признака; – число единиц, значение признака которых изучается.
– число единиц, значение признака которых изучается. , (4.2)
, (4.2) – частота повторения отдельных вариантов признака.
– частота повторения отдельных вариантов признака. . (4.3)
. (4.3) , (4.4)
, (4.4)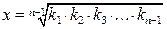 , (4.5)
, (4.5)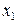 – первый (базисный) уровень ряда динамики;
– первый (базисный) уровень ряда динамики;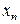 – последний уровень ряда динамики;
– последний уровень ряда динамики;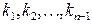 – цепные коэффициенты роста данного ряда динамики.
– цепные коэффициенты роста данного ряда динамики.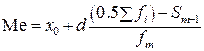 , (4.6)
, (4.6)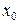 – нижняя граница медианного интервала;
– нижняя граница медианного интервала; – величина медианного интервала;
– величина медианного интервала;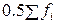 – полусумма частот всех интервалов;
– полусумма частот всех интервалов;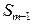 – сумма частот до медианного интервала;
– сумма частот до медианного интервала;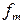 – частота медианного интервала.
– частота медианного интервала. , (4.7)
, (4.7)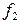 – частота модального интервала;
– частота модального интервала; – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;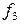 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.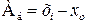 (6.1)
(6.1)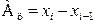 (6.2)
(6.2)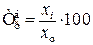 (6.3)
(6.3)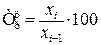 (6.4)
(6.4)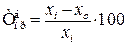 (6.5)
(6.5)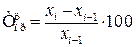 , (6.6)
, (6.6)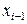 – предшествующий текущему уровень ряда динамики;
– предшествующий текущему уровень ряда динамики;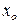 – базисный (начальный) уровень ряда динамики.
– базисный (начальный) уровень ряда динамики.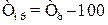 ; (6.7)
; (6.7)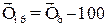 . (6.8)
. (6.8)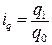 ,
, 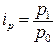 ,
, 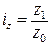 ,
, 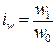 и т.п., (7.1)
и т.п., (7.1)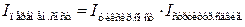 (7.2)
(7.2)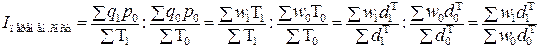 ,
,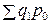 ,
, 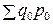 – стоимость произведенной продукции в отчетном и базисном периодах в сопоставимых ценах;
– стоимость произведенной продукции в отчетном и базисном периодах в сопоставимых ценах;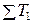 ,
, 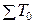 – численность работников в отчетном и базисном периодах. Индекс фиксированного состава:
– численность работников в отчетном и базисном периодах. Индекс фиксированного состава: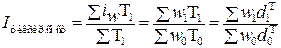 , (7.4)
, (7.4)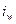 – индивидуальные индексы производительности труда.
– индивидуальные индексы производительности труда.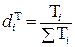 (7.5)
(7.5)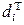 . В других индексах могут использоваться показатели
. В других индексах могут использоваться показатели 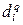 ,
, 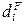 и т.д.
и т.д.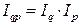 , (7.6)
, (7.6)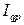 – индекс стоимости продукции;
– индекс стоимости продукции;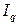 – индекс физического объема продукции в базисных ценах;
– индекс физического объема продукции в базисных ценах;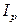 – индекс цен.
– индекс цен.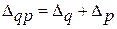 . (7.6а)
. (7.6а)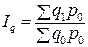 ; (7.7)
; (7.7)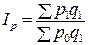 ; (7.8)
; (7.8)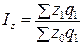 . (7.9)
. (7.9)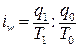 ,
, 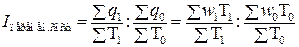 ; (7.10)
; (7.10)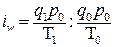 ,
, 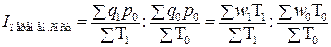 ,
,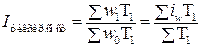 ; (7.11)
; (7.11)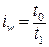 ,
, 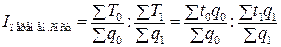 ,
, , (7.12)
, (7.12)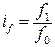 ,
, 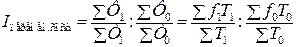 ,
,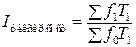 , (7.13)
, (7.13)


