
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Распределение признака в совокупностиСодержание книги
Поиск на нашем сайте
Приступая к изучению темы, необходимо прежде всего составить себе представление о происхождении различия в величине количественного признака у отдельных единиц изучаемого явления в пределах однородной совокупности. Далее следует усвоить приемы построения ряда распределения при изучении вариации дискретных и непрерывно изменяющихся признаков. Для измерения вариации (колеблемости) признака могут быть использованы следующие показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и коэффициент вариации. Три последних показателя обладают преимуществами, обусловленными их математическими свойствами, перед первыми двумя. размах вариации
среднее линейное отклонение
Дисперсией называется средний квадрат отклонений вариантов от их средней величины. Формула расчета:
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии, т.е.
Этот показатель измеряет абсолютный размер колеблемости признака и выражается в тех же единицах измерения, что и значения признака. Коэффициент вариации позволяет сравнивать колеблемость (вариацию) различных, но взаимосвязанных явлений (или их признаков), а также колеблемость одноименных признаков, но действующих в различных условиях места или времени. Формула расчета:
При рассмотрении показателя дисперсии необходимо обратить внимание на правило сложения дисперсий. Тема 6. Ряды динамики Задача темы – изучение методов построения статистических показателей, характеризующих изменение явлений во времени. В процессе изучения темы надо представить сущность рядов динамики и усвоить правила их построения, соблюдение которых обеспечивает сопоставимость статистических рядов динамики и позволяет осуществить их научный анализ. В процессе анализа используются аналитические и обобщающие показатели рядов динамики: уровень ряда, абсолютный прирост, темпы роста и прироста, значение одного процента прироста, коэффициенты опережения и ускорения. Абсолютный прирост: · базисный · цепной Темп роста: · базисный · цепной Темп прироста: · базисный · цепной где
При рассмотрении приемов обработки и анализа данных ряда динамики следует использовать знание принципов взаимосвязи между показателями ряда динамики: · произведение ряда последовательных цепных коэффициентов роста равно соответствующему базисному коэффициенту роста; · частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту; · темп прироста может быть рассчитан путем вычитания ста (процентов) из соответствующего значения показателя темпа роста:
· абсолютное значение 1 %прироста составляет 0,01 предшествующего уровня ряда динамики. Для получения аналитических характеристик ряда динамики исчисляются и средние показатели. Средний уровень периодического ряда динамики и средний абсолютный прирост определяют по формуле средней арифметической. Средний уровень моментного ряда исчисляется по формуле средней хронологической. Средний темп роста определяется по формуле средней геометрической, а средний темп прироста равняется соответствующему среднему темпу роста минус 100:
Особое внимание следует уделить изучению закономерностей изменения ряда в целом: сглаживанию и выравниванию рядов динамики, интерполяции и экстраполяции. Тема 7. Индексы При изучении содержания темы студент должен составить представление об индексе как показателе сравнения двух величин; элементах, входящих в построение индексов; различиях индексов индивидуальных и агрегатных, индексов объемных и качественных показателей. Основное внимание должно быть уделено агрегатным индексам – показателям сравнения характеристик сложных явлений, состоящих из непосредственно не суммируемых элементов. Надо усвоить методику построения агрегатных индексов физического объема продукции. Следует иметь в виду, что основной проблемой при построении этих индексов является проблема выбора показателей-соизмерителей, обеспечивающих сопоставимость числителя и знаменателя индекса. Индексируемые показатели, а также явления, выступающие в роли соизмерителей, могут быть качественными и количественными (объемными). Количественные показатели представляют собой численность тех или иных единиц или общий объем какого-либо признака. Качественные характеризуют уровень явления в расчете на ту или иную единицу совокупности. При построении агрегатных индексов качественных показателей в роли соизмерителей выступают количественные показатели и фиксируются на уровне отчетного периода. При построении агрегатных индексов количественных показателей в роли соизмерителей выступают качественные показатели и фиксируются на уровне базисного периода. Индивидуальные индексы не требуют соизмерителей, т.к. при их расчете сравниваются абсолютно однородные явления:
где q – количество единиц продукции одного вида (шт., т, л,...); p – цена единицы определенного вида продукции (руб.); z – себестоимость единицы определенного вида продукции (руб.); w – производительность труда одного человека (шт., т, л,...). Средние индексы (арифметический, гармонический) студент изучает в связи с агрегатными. Агрегатные индексы качественных показателей применяются в двух формах: в форме индексов переменного состава и в форме индексов фиксированного состава. Индекс среднего уровня может быть представлен как произведение аналитических индексов-сомножителей, каждый из которых отражает изменение только одного фактора, и тем самым – влияние этого изменения на динамику среднего уровня. Первый индекс носит название индекса фиксированного состава, второй – индекса структурных сдвигов.
Например, для анализа динамики среднемесячной производительности труда (w) по группе работников индекс переменного состава определяется по формуле:
(7.3) где
где Индексы, приведенные в формуле (7.4), являются индексами фиксированного состава, т.к. в каждом из них индексируется только одна величина; напротив, индексы, приведенные в формуле (7.3), характеризуют изменение и качественных величин (w), и структуры количественных (T). Эта структура может быть выражена в виде относительных величин:
В дальнейшем, для отражения отличия структуры показателя Т (либо других количественных показателей) в разных условиях, будет применяться обозначение Индексные методы широко применяются для анализа факторов изменения сложных показателей, полученных на основе соизмерения абсолютных величин. В связи с этим необходимо изучить вопрос о способах построения взаимосвязанных индексов и способах расчета абсолютного изменения сложной величины за счет влияющих факторов. Индекс результативного показателя связан с индексами показателей-факторов так же, как абсолютные величины этих показателей:
где
Такая взаимосвязь может быть использована не только для выявления относительного изменения уровня изучаемого явления за счет отдельных факторов, но и для определения размера абсолютного изменения уровня сложного явления в связи с влиянием исследуемых факторов:
Среди наиболее часто используемых в экономических расчетах индексов необходимо отметить: индексы объема
индексы цен
индексы себестоимости
Индексы производительности труда могут иметь три формы: натуральные
стоимостные
трудовые
где t – трудоемкость изготовления единицы продукции. Индексы заработной платы также имеют две формы (индивидуальный индекс и сводный индекс), т.к. заработная плата – это сумма, начисленная в счет оплаты за работу одного человека, т.е. показатель качественный:
где Ф – фонд заработной платы всех работников на исследуемом объекте, f – заработная плата одного работника. В выше приведенных формулах использованы условные обозначения любого учебника «Общей теории статистики». Завершая изучение темы, следует обратить внимание на наличие взаимосвязей между следующими группами индексов: - индивидуальными и сводными; - индексами базисными и цепными; - индексами переменного и фиксированного состава; - индексами взаимосвязанных явлений.
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.125.86 (0.01 с.) |

 , (5.1)
, (5.1) . (5.2)
. (5.2) . (5.3)
. (5.3) . (5.4)
. (5.4) . (5.5)
. (5.5)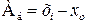 (6.1)
(6.1)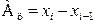 (6.2)
(6.2)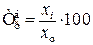 (6.3)
(6.3)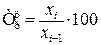 (6.4)
(6.4)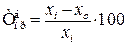 (6.5)
(6.5)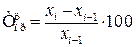 , (6.6)
, (6.6)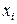 – текущий уровень ряда динамики;
– текущий уровень ряда динамики;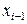 – предшествующий текущему уровень ряда динамики;
– предшествующий текущему уровень ряда динамики;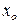 – базисный (начальный) уровень ряда динамики.
– базисный (начальный) уровень ряда динамики.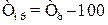 ; (6.7)
; (6.7)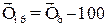 . (6.8)
. (6.8)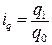 ,
, 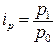 ,
, 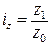 ,
, 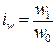 и т.п., (7.1)
и т.п., (7.1)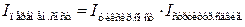 (7.2)
(7.2)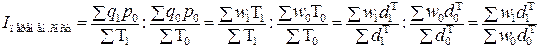 ,
,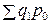 ,
, 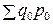 – стоимость произведенной продукции в отчетном и базисном периодах в сопоставимых ценах;
– стоимость произведенной продукции в отчетном и базисном периодах в сопоставимых ценах;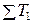 ,
, 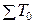 – численность работников в отчетном и базисном периодах. Индекс фиксированного состава:
– численность работников в отчетном и базисном периодах. Индекс фиксированного состава: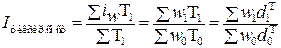 , (7.4)
, (7.4)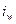 – индивидуальные индексы производительности труда.
– индивидуальные индексы производительности труда.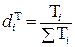 (7.5)
(7.5)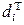 . В других индексах могут использоваться показатели
. В других индексах могут использоваться показатели 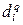 ,
, 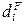 и т.д.
и т.д.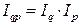 , (7.6)
, (7.6)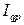 – индекс стоимости продукции;
– индекс стоимости продукции;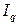 – индекс физического объема продукции в базисных ценах;
– индекс физического объема продукции в базисных ценах;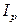 – индекс цен.
– индекс цен.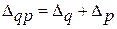 . (7.6а)
. (7.6а)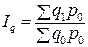 ; (7.7)
; (7.7)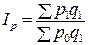 ; (7.8)
; (7.8)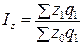 . (7.9)
. (7.9)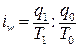 ,
, 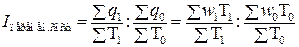 ; (7.10)
; (7.10)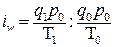 ,
, 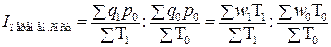 ,
,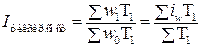 ; (7.11)
; (7.11)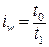 ,
, 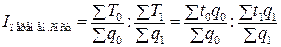 ,
, , (7.12)
, (7.12)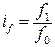 ,
, 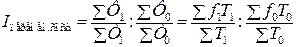 ,
,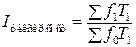 , (7.13)
, (7.13)


