
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения о корреляционной связиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте И ее статистическом изучении Часто в практике производства одежды при работе с текстильными материалами приходится судить об их свойствах по уже известным свойствам, либо характеристикам структуры. Очень важно знать и уметь оценить такую взаимосвязь. Исследовать закономерности связей между явлениями (процессами), которые зависят от многих факторов, позволяет корреляционный анализ. Корреляция изучается на основании экспериментальных данных, представляющих собой измеренные значения Корреляционный анализ, как и другие статистические методы, основан на использовании вероятностных моделей, описывающих поведение исследуемых признаков в некоторой генеральной совокупности, из которой получены экспериментальные значения При исследовании корреляции между количественными признаками, значения которых можно точно измерить в единицах метрических шкал (метры, секунды, килограммы и т. д.), то часто принимается модель двухмерной нормально распределенной генеральной совокупности. Такая модель отображает зависимость между переменными величинами Существует три вида корреляции – линейная, нелинейная и множественная. При линейной корреляции линия регрессии аппроксимируется уравнением прямой, при нелинейной – уравнением кривой. Если измеряются связи между двумя признаками – парная корреляция, между тремя и более – множественная корреляция. Наиболее распространенной является линейная корреляция. Наиболее важным является коэффициент корреляции. Коэффициент парной корреляции
где Значение коэффициента корреляции всегда меньше или равно единице (рис.6.1):
Значения
Рис. 6.1. Значение коэффициента корреляции Значение
Оценка производится путем сравнения полученной величины Обычно считают тесноту связи удовлетворительной при Пример вычисления и статистической оценки Существенности параметров парной линейной корреляции
Пусть необходимо оценить взаимосвязь между линейной плотностью нитей и разрывной нагрузкой по основе пальтовых тканей, показатели которых представлены в табл. 6.1. [3] Таблица 6.1 Показатели структуры и свойств пальтовых тканей
Чтобы предварительно определить наличие такой связи, необходимо построить график точек, соответствующих сочетанию показателей свойств – корреляционное поле точек (рис. 6.2). По тесноте группирования точек можно судить о наличии корреляционной связи. Если нанести на корреляционном поле средние значения
Рис. 6.2. Корреляционное поле точек
Критерием близости корреляционной зависимости Коэффициент корреляции рассчитываем по формуле (6.1).
Для упрощения промежуточных вычислений и расчета коэффициента используем табл. 6.2. Таблица 6.2 Расчеты для определения коэффициента корреляции
Для контроля существования корреляционной зависимости рассчитываем критерий Стьюдента
Полученное значение Значение коэффициента корреляции
Практическая работа № 6 Тема работы: определение корреляционной зависимости между параметрами технологического процесса Цель работы: ознакомиться с методикой определения коэффициента линейной корреляции и оценить взаимосвязь между свойствами тканей в соответствии с заданием. Методика и порядок выполнения: 1. В соответствии с полученным заданием (табл. 6.3) выбрать из табл. 6.4 значения показателей свойств материалов, оформив данные в виде табл. 6.1. Таблица 6.3 Задания к практической работе 6
2. Провести предварительный анализ на наличие и вид связи между заданными переменными, нанеся точки на график и построив корреляционное поле. 3. Рассчитать коэффициент парной корреляции 4. Провести контроль существования корреляционной зависимости по критерию Стьюдента 5. Оценить тесноту связи между свойствами.
Значения показателей свойств материалов
Содержание отчета 1. Данные показателей свойств, выбранные в соответствии с вариантом задания в виде табл. 6.1. 2. График с построенным корреляционным полем для заданных свойств материалов с предварительным анализом наличия связи между ними. 3. Результаты расчета коэффициента корреляции 4. Расчет критерия Стьюдента 5. Вывод о тесноте связи между рассматриваемыми свойствами. Корреляционная зависимость, являясь частным случаем статистической зависимости, характеризует взаимосвязь значений одних случайных величин со средним значением других. Корреляционный анализ позволяет установить направление и форму связи между признаками, измерить ее тесноту и оценить достоверность выборочных показателей корреляции. Контрольные вопросы 1. Что такое корреляционный анализ? 2. Дать определение корреляционной связи (корреляции) признаков. 3. Какие виды корреляции вам известны? 2. Приведите примеры корреляционной зависимости. 3. Как проводится контроль существования корреляционной зависимости? 4. Что характеризует коэффициент корреляции и как он определяется? 5. Каким показателем характеризуется теснота связи? 6. Как проводится статистическая оценка надежности коэффициента парной линейной корреляции?
ЭКСПЕРТНЫ Е МЕТОДЫ ОЦЕНКИ КАЧЕСТВА ПРОДУКЦИИ В настоящее время значение величины технологических и качественных показателей швейных изделий могут быть определены методами технических и эвристическ их (эвристика – система логических приемов и методических правил теоретического исследования) измерений. Оба эти метода нашли широкое применение при разработке новых материалов, конструкций, технологических решений в швейной промышленности. Определяющими факторами при выборе метода измерения являются количество и достоверность информации об объекте, а также простота, надежность и доступность самого метода [1, с. 183–196].
Методы измерения при оценке
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

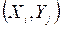 двух признаков.
двух признаков. и
и  .
. характеризует тесноту связи между двумя случайными величинами в случае линейной корреляции между ними, и рассчитывается по формуле:
характеризует тесноту связи между двумя случайными величинами в случае линейной корреляции между ними, и рассчитывается по формуле: , (6.1)
, (6.1) – значения переменных величин;
– значения переменных величин; 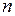 – количество измерений.
– количество измерений.


 указывают на строгую функциональную – положительную или отрицательную – линейную связь. При положительном значении
указывают на строгую функциональную – положительную или отрицательную – линейную связь. При положительном значении  одна из величин возрастает – когда возрастает другая, и убывает – когда убывает другая. Если
одна из величин возрастает – когда возрастает другая, и убывает – когда убывает другая. Если 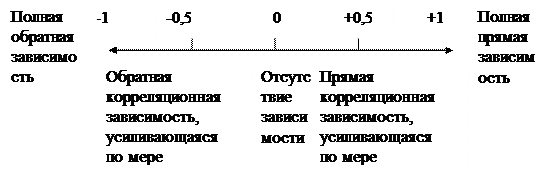
 указывает на отсутствие линейной корреляции между величинами. Для значений коэффициента корреляции, находящихся между 0 и –1 или +1 нужно дополнительное исследование. Существование корреляционной зависимости контролируют по критерию Стьюдента (
указывает на отсутствие линейной корреляции между величинами. Для значений коэффициента корреляции, находящихся между 0 и –1 или +1 нужно дополнительное исследование. Существование корреляционной зависимости контролируют по критерию Стьюдента ( -распределение):
-распределение): . (6.2)
. (6.2)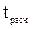 с табличным значением
с табличным значением  (прил. 2). Если рассчитанная величина
(прил. 2). Если рассчитанная величина  , хорошей при
, хорошей при  .
.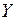 , то проведенная линия будет являться линией регрессии. На рисунке видна определённая связь между переменными
, то проведенная линия будет являться линией регрессии. На рисунке видна определённая связь между переменными 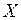 и
и 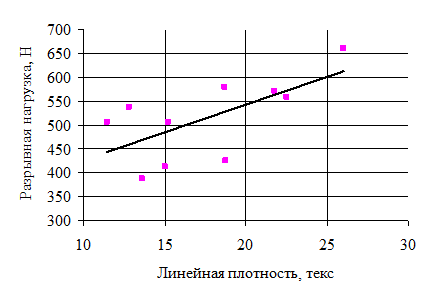
 .
.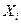



 по формуле (6.2).
по формуле (6.2). .
. больше табличного значения
больше табличного значения  (прил. 2) при числе степеней свободы равном
(прил. 2) при числе степеней свободы равном 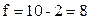 и доверительной вероятности 0.95, что свидетельствует о существовании корреляционной зависимости между рассматриваемыми параметрами.
и доверительной вероятности 0.95, что свидетельствует о существовании корреляционной зависимости между рассматриваемыми параметрами.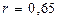 , при значении критерия
, при значении критерия  по формуле (6.1), представив расчеты в виде табл. 6.2.
по формуле (6.1), представив расчеты в виде табл. 6.2. по формуле (6.2).
по формуле (6.2). Таблица 6.4
Таблица 6.4



