
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение двухмерных сечений поверхности откликаСодержание книги
Поиск на нашем сайте
На практике, как правило, большинство задач связано с учетом большого числа факторов ( Знание двухмерных сечений поверхности отклика дает возможность получить наглядное представление о законах изменения критерия отклика при варьировании факторов, облегчает интерпретацию результатов эксперимента, способствующих решению компромиссных задач графическим методом. Для построения двухмерных сечений поверхности используют адекватные математические модели объекта исследований, при этом в известное уравнение регрессии подставляют значение всех факторов, кроме двух (факторы, которые фиксируются, рекомендуется брать на оптимальных уровнях). В результате для выбранной пары факторов получают обычно уравнение типа:
С помощью этих уравнений находят графические зависимости путем построения в области эксперимента линий равных значений отклика, относящихся к рассматриваемому сечению поверхности отклика. Построение двухмерных сечений поверхности отклика состоит из нескольких этапов. 1. Определение координат нового центра. Координаты нового центра в старых осях координат (xis, xjs) получают дифференцированием уравнения регрессии по каждой независимой переменной и приравниванием частных производных к нулю:
Вычисляют определитель системы:
Решая систему уравнений (5.8), определяют координаты нового центра S в старых осях координат xis и xjs. Подставив значения xis и xjs в уравнение регрессии, находят значение параметра оптимизации (ys) в новом центре. Не меняя направления осей координат, переносят начало координат в точку
Получают уравнение кривой в новой системе координат (
2. Определение угла поворота осей координат в новом центре. Для исключения парного взаимодействия факторов определяют угол поворота осей координат в точке
где 3. Определение коэффициентов уравнения регрессии в канонической форме. Коэффициенты уравнения регрессии в канонической форме рассчитывают с помощью следующих уравнений:
В результате канонического преобразования получают стандартное уравнение вида:
Правильность расчетов при каноническом преобразовании оценивают сравнением суммы коэффициентов при квадратичных членах в уравнении регрессии и в каноническом уравнении:
4. Определение вида поверхности отклика. По уравнению (5.16) определяют, к какому типу относится геометрический образ изучаемой функции отклика. 5. Построение сечений поверхности отклика. Уравнение (5.16) приводят к каноническому уравнению линии равного значения отклика соответствующей стандартной поверхности. Подставляя в уравнение (5.16) различные значения параметра оптимизации, задаваемые в пределах области эксперимента через равные промежутки, получают уравнения, по которым строят контурные кривые. Результаты расчетов сводят в табл. 5.1.
Таблица 5.1 Данные для построения контурных кривых
Рассмотрим пример построения двухмерного сечения в виде эллипса. При исследовании процесса получения сварных соединений найдено уравнение регрессии второго порядка для
Так как трудно представить геометрический образ для всех трех факторов, исследование проводится с помощью двух факторов, например, Подставив в уравнение (5.18) значение
Определяют координаты нового центра. Для этого уравнение дифференцируют это по

Вычисляют определитель системы:
Определитель не равен нулю, следовательно, исследуемая поверхность имеет центр.
Решают систему уравнений (4.19) методом подстановки, вычисляют координаты нового центра в старых осях координат: Подставляя в уравнение (5.19) вместо
Переносим начало системы координат После переноса начала координат в новый центр уравнение примет вид:
Для исключения парного взаимодействия факторов определяют угол поворота осей координат в точке:
Далее определяют коэффициенты регрессии в канонической форме.
В результате получается уравнение в канонической форме
Практика подтверждает точность расчетов (4.16):
Проводятся старые оси координат
где
Координаты нового центра в старых осях координат в точке S(4,58; 0,81). Производится поворот осей координат в точке 0 на величину угла Построение линий равного значения отклика осуществляется в новой системе координат При
Преобразуем это уравнение в стандартную форму:
Оба коэффициента уравнения положительны, центр фигуры является максимумом, а вытянут эллипс вдоль оси
Рис. 5.2. Контуры кривых с равными значениями параметра оптимизации – эллипса Таблица 5.2 Данные для построения контурных кривых поверхности отклика
После построения кривых поверхности отклика проводится их анализ, и определяются значения факторов, соответствующие оптимальным значениям параметра оптимизации.
Практическая работа № 5
Тема работы: Построение геометрическойповерхности отклика по результатам исследования технологического процесса. Цель работы: Ознакомится с методикой построения сечений поверхности отклика, и определить закономерность измерения критерия оптимизации при варьировании факторов. Методика и порядок выполнения: 1. Ознакомиться с методом построения двухмерных сечений поверхностей отклика. 2. Получить задание на вид математической модели процесса (объекта), полученной после реализации матрицы планирования и расчета коэффициентов регрессии (табл. 5.3). Представленные математические модели найдены в результате исследования технологического процесса сварки с использованием центрального композиционного ротатабельного планирования второго порядка. Выявлена зависимость прочности и жесткости сварных соединений от параметров режима сварки (давление электродов на материал, времени сварки и напряженности электрического поля, характеризуемой силой анодного тока) (табл. 5.4) [16, с. 113–124].
Таблица 5.3 Задания для построения поверхности отклика
Таблица 5.4 Интервалы и уровни варьирования факторов для сварки материалов
3. Определить координаты нового центра 4. Определить угол поворота осей координат в новом центре 5. Определить коэффициенты уравнения регрессии в канонической форме (5.13)–(5.15) и записать стандартное уравнение вида (5.16). 6. Определить вид поверхности отклика. 7. Построить сечения поверхности отклика.
8. В выводах делается анализ поверхности отклика, указываются оптимальные значения факторов.
Содержание отчета по практической работе № 5 1. Интервалы и уровни варьирования факторов для заданного варианта (табл. 4.3), уравнение регрессии. 2. Расчет координат нового центра и угла поворота осей координат в новом центре. 3. Уравнение регрессии в канонической форме. 4. Характеристика вида поверхности отклика. 5. Расчет данных для построения контурных кривых поверхности отклика, представленный в виде табл. 5.1. 6. Рисунок с построением сечений поверхности отклика. 7. Выводы по работе. Знание двухмерных сечений поверхностей отклика позволяет судить о закономерностях изменения критерия оптимизации при варьировании факторов, облегчает интерпретацию результатов эксперимента, способствует решению компромиссных задач графическим методом. Контрольные вопросы 1. С какой целью выполняется каноническое преобразование уравнений? 2. В чем заключается каноническое преобразование уравнений второй степени? 3. Как определяют положение нового центра в старых осях координат? 4. Как производится поворот осей координат? 5. Как определяют вид поверхности отклика? 6. Какова последовательность построения двухмерных сечений? 7. Какую информацию дает анализ семейства кривых?
В промышленности и научных исследованиях проводятся опыты, с тем чтобы посредством изменений в технологии повысить качество производимого продукта. При этом исходят из предположения, что изменение независимого признака ( Корреляционное исчисление применяется только там, где переменные не подвергаются влиянию со стороны эксперимента, и представляют, следовательно, случайные переменные, в то время как регрессивное исчисление применяется там, где одна переменная
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 863; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.223.185 (0.013 с.) |

 ), поэтому полученные при этом канонические уравнения громоздки, их анализ затруднен. Кроме того, их построение связано с вычислениями, которые требуют значительных затрат времени. В связи с этим при решении практических задач целесообразно изучать геометрические поверхности, соответствующие найденным математическим моделям с помощью двухмерных сечений указанных поверхностей.
), поэтому полученные при этом канонические уравнения громоздки, их анализ затруднен. Кроме того, их построение связано с вычислениями, которые требуют значительных затрат времени. В связи с этим при решении практических задач целесообразно изучать геометрические поверхности, соответствующие найденным математическим моделям с помощью двухмерных сечений указанных поверхностей. (5.7)
(5.7) (5.8)
(5.8)
 . (5.9)
. (5.9)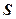 , используя соотношения
, используя соотношения и
и  (5.10)
(5.10) )
) . (5.11)
. (5.11) по формуле
по формуле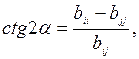 (5.12)
(5.12)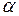 – угол поворота осей координат (знак «+» – поворот осей координат от оси
– угол поворота осей координат (знак «+» – поворот осей координат от оси  вверх, знак «–» – вниз).
вверх, знак «–» – вниз). (5.13)
(5.13) (5.14)
(5.14) (5.15)
(5.15) (5.16)
(5.16) (5.17)
(5.17)
 , являющееся адекватной математической моделью:
, являющееся адекватной математической моделью: (5.18)
(5.18)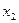 и
и  . Фиксирование значения третьего фактора осуществляется на нулевом уровне, т.е.
. Фиксирование значения третьего фактора осуществляется на нулевом уровне, т.е. 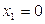 .
. (5.19)
(5.19)
 .
. ,
,  .
. и
и  координаты центра
координаты центра  и
и  , получают значение параметра оптимизации
, получают значение параметра оптимизации 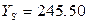 в центре поверхности отклика:
в центре поверхности отклика:
 в центр фигуры. При параллельном переносе системы координат в центр фигуры в исходном уравнении исчезают члены, содержащие линейные эффекты, и изменяется свободный член. Коэффициенты других членов не изменяются. В новой системе координат свободный член уравнения равен значению параметра оптимизации
в центр фигуры. При параллельном переносе системы координат в центр фигуры в исходном уравнении исчезают члены, содержащие линейные эффекты, и изменяется свободный член. Коэффициенты других членов не изменяются. В новой системе координат свободный член уравнения равен значению параметра оптимизации 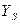 в центре фигуры.
в центре фигуры. (5.21)
(5.21)


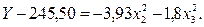 (5.22)
(5.22)
 и
и  (5.23)
(5.23) – натуральное значение
– натуральное значение  -го фактора;
-го фактора;  – натуральное значение основного уравнения
– натуральное значение основного уравнения  – интервал варьирования
– интервал варьирования 



 , а затем параллельный перенос осей координат в новый центр (точку
, а затем параллельный перенос осей координат в новый центр (точку  ).
).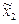
 . Значения параметра оптимизации выбираются через равные промежутки с учетом величин параметра оптимизации в области эксперимента.
. Значения параметра оптимизации выбираются через равные промежутки с учетом величин параметра оптимизации в области эксперимента. уравнение (5.21) принимает вид:
уравнение (5.21) принимает вид: .
. или
или  .
.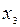 (величина этого коэффициента минимальна).Эллипс пересекается осью
(величина этого коэффициента минимальна).Эллипс пересекается осью  в двух точках А(
в двух точках А( ), а с осью
), а с осью  – В(
– В( ). От точки
). От точки  по оси
по оси 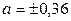 ; затем по оси
; затем по оси 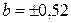 в кодированных величинах. Полученные точки соединяют плавной кривой. Для более точного построения можно найти еще несколько промежуточных точек, например, задаемся значением
в кодированных величинах. Полученные точки соединяют плавной кривой. Для более точного построения можно найти еще несколько промежуточных точек, например, задаемся значением  и получаем точку С(
и получаем точку С( ) и т.д. Аналогично строят другие контурные линии. Основой для построения служат данные табл. 5.2, получаемые подстановкой различных значений параметра оптимизации в уравнение (5.22). Кривые с равными значениями параметра оптимизации – эллипса приведены на рис. 5.2.
) и т.д. Аналогично строят другие контурные линии. Основой для построения служат данные табл. 5.2, получаемые подстановкой различных значений параметра оптимизации в уравнение (5.22). Кривые с равными значениями параметра оптимизации – эллипса приведены на рис. 5.2.
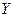

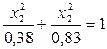







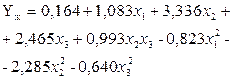





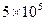





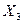
 ,
,  ) в результате решения системы уравнений (5.8); вычислить значение параметра оптимизации (
) в результате решения системы уравнений (5.8); вычислить значение параметра оптимизации (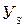 ) в новом центре.
) в новом центре. 6. корреляционный анализ
6. корреляционный анализ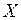 ) влияет на зависимый от него признак (
) влияет на зависимый от него признак (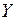 ), и проверяют правильность этого предположения по результатам испытания. Результаты испытаний, если предполагается линейная зависимость, находятся не на прямой. Из-за погрешностей в технологии они рассеиваются вокруг этой прямой, т. е. представляют собой так называемое облако. В этом случае часто бывает трудно визуально решить, можно ли говорить о зависимости между различными признаками или нет, тем более что из-за неподходящего выбора масштабов по осям координат имеющиеся зависимости могут затушевываться, а не имеющиеся – казаться существующими. Математико-статистическим критерием оценки доказательства таких зависимостей является корреляционно-регрес-сивное исчисление.
), и проверяют правильность этого предположения по результатам испытания. Результаты испытаний, если предполагается линейная зависимость, находятся не на прямой. Из-за погрешностей в технологии они рассеиваются вокруг этой прямой, т. е. представляют собой так называемое облако. В этом случае часто бывает трудно визуально решить, можно ли говорить о зависимости между различными признаками или нет, тем более что из-за неподходящего выбора масштабов по осям координат имеющиеся зависимости могут затушевываться, а не имеющиеся – казаться существующими. Математико-статистическим критерием оценки доказательства таких зависимостей является корреляционно-регрес-сивное исчисление.


