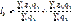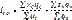Агрегатный индекс как исходная форма индексов

А.и.-сложный относительный показатель, характеризующий среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов.

В числителе и знаменателе а.и.содержатся соединенные наборы элементов изучаемых совокупностей. Достижение в сложных статистических совокупностях сопоставимости разнородных единиц осуществляется введением в индексные отношения специальных сомножителей индексируемых величин.

индексируемая величина -значение признака стат.совокупности, изменение которого является объектом изучения.

Вес индекса - это величина, служащая для целей соизмерения индексируемых величин.

При выборе веса индекса руководствуются следующим правилом:

- индекс количественного (объемного) показателя строится при неизменных весах базисного периода, которыми выступают качественные показатели.

- индекс качественного показателя строится при неизменных весах отчетного периода, которые выражаются объемными показателями.

Например агрегатные индексы можно представить в след.виде.

агрегатный индекс себестоимости:

агрегатный индекс производительности труда:

агрегатный индекс производственных затрат:

Индекс Пааше

При сравнении числителя и знаменателя формулы в разности определяется показатель абсолютного прироста оборота торговли за счет фактора изменения цен в текущем периоде по сравнению с базисным периодом:

Данный индекс используется при определении индекса дефлятора ВВП

Индекс Ласпейреса

При сравнении числителя и знаменателя формулы определяется показатель прироста товарооборота при продаже товаров в базисном периоде по цена текущего периода:

Индекс цен Фишера («идеальный» индекс)

I_p= I_p*I_p

Средние индексы

Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов.

Средние общие индексы получают путем преобразования агрегатных индексов. Агрегатный индекс может быть преобразован в средний арифметический или средний гармонический. Форму средней нужно выбрать таким образом, чтобы полученный средний индекс был тождественен исходному агрегатному индексу. Средний арифметический индекс тождественен агрегатному индексу если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Средний гармонический индекс тождественен агрегатному, если весами индивидуальных индексов будут слагаемые числителя агрегатного индекса.

Средние индексы применяют, если не известны значения отдельных и индексируемых явлений и их весов в отчетном или базовом периодах, но известны их изменения, которые могут быть представлены в виде индивидуальных индексов. Таким образом, если анализируется изменение объема, то пользуются обычно среднеарифметическим взвешенным индексом, например:

Если анализируется изменение качественного показателя, то обычно используется среднегармонический индекс, например, индекс себестоимости:

Индексы средних величин

При анализе изменения средних уровней пользуются индексами переменного, постоянного состава и структурных сдвигов. Например:

- индекс переменного состава (индекс средней себестоимости):

- индекс постоянного состава (индекс изменения себестоимости отдельных элементов совокупности):

- индекс структурных сдвигов:

24. Виды и формы взаимосвязи между явлениями

Связи между признаками и явлениями классифицируются по ряду оснований:

1) по степени зависимости одного явления от другого различают функциональную и стохастическую связь.

Функциональной называется связь, при которой определенному значению фактор-ного признака соответствует одно строго определенное значение результативного при-знака. Наиболее часто функциональные связи проявляются в естественных науках, на-пример, в механике функциональной является зависимость расстояния, пройденного объектом, от скорости его движения.

Стохастической называется связь, при которой каждому значению признака х со-ответствует множество значений признака y. Статистическая связь проявляется лишь «в общем и среднем» при большом числе наблюдений за явлением.

Корреляционной является статистическая связь между признаками, при которой изменение значений независимой переменной X приводит к закономерному изменению математического ожидания случайной величины Y.

2) по направлению различают прямую и обратную связь.

Прямой называется связь, при которой с ростом значений факторного признака возрастают значения результативного признака.

При обратной связи с увеличением значения одного признака величина другого признака, зависящего от него, уменьшается.

3) по аналитическому выражению различают линейные и нелинейные связи.

Линейная – связь, которая может быть аналитически выражена уравнением пря-мой линии.

Нелинейная (криволинейная) – связь, которая может быть выражена уравнением какой-либо кривой.

25. Способы выявления и хар-ки взаимосвязей

Для выявления наличия связи, ее характера и направления в статистике использу-ются следующие методы:

1)метод сопоставления параллельных рядов. При этом методе данные сопоставля-ются обычно в табличной форме в виде параллельно расположенных стат. рядов. Значе-ние факторного признака располагается в возрастающем порядке, параллельно записыв-ся значения результативного признака и путем сопоставления выявляют нали-чие/отсутствие связи.

2)балансовый метод. Данные взаимосвязанных показателей излагаются в виде таб-лиц, в которых итоги отд. частей должны быть равны м/у собой. Этот метод использ-ся для выявления взаимосвязей м/у производством и реализацией использования ресурсов предприятия Он+П=Р+Ок

3)метод аналитических группировок позволяет установить наличие м/у двумя и более признаками взаимосвязь, а также ее направление

4)метод дисперсионного факторного анализа дает возм-ть определить значение систематической и случайной вариацией

5)индексный метод факторного анализа отражает компонентные связи

6)по графическому методу можно определить наличие, направление, форму и силу связи.

7)метод таблиц сопряженности основан на построении таблиц, в к-ых дается ком-бинационное распределение единиц совокупности по 2-м альтернативным признакам.