
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели описательной статистикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Переменная (английский термин variabl) – это то, что можно измерять, контролировать или чем можно манипулировать в исследованиях (это то, что варьируется, изменяется, не является постоянным – от английского корня var). Максимум и минимум – это минимальное и максимальное значения переменной. Поскольку значения переменных не постоянны, необходимо описывать их изменчивость. Описательные или дескриптивные статистики включают: вариационные ряды, средние величины (среднее арифметическое, мода и медиана), показатели рассеяния вариант (дисперсия, среднее квадратическое отклонение, коэффициент вариации, квантили, статистические моменты, ассиметрия и эксцесс), оценка статистических параметров по выборочным данным (точечные и интервальные оценки; доверительные - значимость, вероятность, интервал, предел; оптимальная численность выборки). Эти описательные (дескриптивные) статистики дают общее представление о значениях, которое принимает переменная. Вариационные ряды Значительную долю статистических данных составляют количественные признаки, принимающие числовое значение у каждой единицы статистического наблюдения. Числовые значения по каждому признаку варьируют и называются вариантами. Пример: в качестве статистической совокупности взята группа подростков. Каждый подросток – единица наблюдения, а масса тела каждого подростка – вариантой. Масса тела колеблется, варьирует у разных подростков этой статистической совокупности. Для представления этих данных строим ряды распределения. В ходе регистрации массы тела у подростков получаются неупорядоченные ряды отдельных наблюдений. Необходимо провести операцию упорядочения числового ряда массы тела путем ранжирования данных в возрастающем или убывающем порядке. Варианты (варьирующие признаки) могут быть прерывные и непрерывные (дискретные). Наиболее компактной формой описания вариации является образование рядов распределений, где сгруппированы одинаковые или близкие значения. Такой ряд состоит из двух столбцов: в одном располагаются варианты (х), в другом – частоты (р). Частоты показывают, сколько раз встречались одинаковые значения признака. Если ряд распределения состоит из дискретных величин – это дискретный вариационный ряд, если количество значений невелико, его можно представить графически – по оси абсцисс (x) откладываются возможные значения варьирующего признака (в данном примере – массы тела), по оси ординат (y) – число случаев (наблюдений), получается «многоугольник», или так называемый «полигон распределения». Если вариаций признака большое количество (в случае непрерывного ряда), тогда образуют интервальный сгруппированный вариационный ряд. Желательно, чтобы интервалы во всех группах ряда были одинаковы. При этом руководствуются следующими рекомендациями: число групп должно быть нечетным; при числе наблюдений более 100, число групп должно быть в пределах 9-11-13, а при меньшем объеме – 5-7-9. Если величина интервала берется равной для всех групп ряда, то для выведения оптимального интервала группировки необходимо: разницу между максимальным и минимальным значением вариант в ряду разделить на число групп, которое хотят получить, а затем полученную величину округлить – это и есть интервал. Границы каждой группы должны отличаться от границ соседних групп для того, чтобы не было путаницы при отнесении варианты в ту или иную группы (т.е. они не должны казаться одинаковыми). Дальнейшая статистическая обработка такого ряда заключается в определении середины в каждой группе ряда (полусумма крайних значений группы), а если ряд распределения непрерывный - то берется полусумма начальных вариант данной и последующих групп (графическое отображение - гистограмма распределения). Статистические совокупности с количественной стороны могут быть охарактеризованы не только относительными величинами (коэффициентами), которые характеризуют частоту (интенсивность), а также не только состав изучаемого явления, но и при помощи средних величин. Средние величины – это параметры, которые характеризуют распределение ряда положением его середины. Средняя величина выражает характерную, типичную для данного ряда величину признака. Среднее (или среднее арифметическое, или выборочное среднее) – сумма значений переменной Х, деленная на n (число значений переменной). Выборочное среднее обозначается
Выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0. Формально это записывается следующим образом:
Выборочное среднее имеет 2 свойства: сумма отклонений наблюдаемых значений от среднего арифметического действительно равна 0; сумма квадратов расстояний между наблюдаемыми значениями и их средним арифметическим является минимальным. Если вместо среднего арифметического взять любую другую величину, то сумма квадратов расстояний между наблюдаемыми значениями и этой величиной будет только больше, но никак не меньше. Помимо среднего арифметического для характеристики центра распределения используются и другие средние величины: среднее геометрическое, среднее гармоническое, среднее квадратическое. При небольшой вариабельности разница между этими средними практически незаметна. Среднее гармоническое применяется, когда имеют дело с обратными величинами (коли-индекс и пр.); среднее квадратическое вычисляется в том случае, если исходный ряд чисел представлен вариантами, отражающими значения площадей; среднее геометрическое - когда имеется числовой ряд, значения которого распределяются в геометрической прогрессии, резко отличаются друг от друга. Мода и медиана. Выбор характеристик среднего уровня зависит от распределения вариант в вариационных рядах. В ряде случаев целеообразно использовать так называемые структурные средние. К ним относятся мода (Мо) и медиана (Ме). Мода – максимально часто встречающееся значение переменной (наиболее «модное» значение переменной, термин впервые введен Пирсоном в 1894 г.). Если распределение имеет несколько мод, то говорят, что оно мультимодально (имеет два или более «пика»). Мультимодальность может означать, что существуют несколько определенно различных мнений, она также служит индикатором того, что выборка не является однородной и наблюдения, возможно, порождены двумя или более «наложенными» распределениями. Медиана дает представление о том, где находится центр переменной, она разбивает выборку на 2 равные части, половина значений переменной лежит ниже медианы, половина – выше. Наблюдения упорядочиваются по возрастанию:
Полученная последовательность Если число наблюдений четно n=2m, то в качестве оценки медианы берется величина ( Свойство медианы: сумма абсолютных расстояний между точками выборки и медианой минимальна. С вариационным рядом связано много важных статистик, например, спейсинги, представляющие собой расстояния между соседними порядковыми статистиками. Показатели рассеяния вариант После получения обобщенных характеристик вариационного ряда следует установить его колеблемость – размеры варьирования признака. Простейшими количественным характеристиками здесь являются лимит и аплитуда. Лимит (Lim) показывает границы вариационного ряда «от и до». Амплитуда (Ampl) исчисляется, как разность между максимальным и минимальным значениями признака. Недостаток лимита и амплитуды, как характеристик вариабельности ряда, заключается в том, что они зависят только от крайних значений и не учитывают колебаний значения признака внутри ряда. Удобнее и проще оценить однородность числового ряда через отклонения каждого значения от среднего арифметического Дисперсия (D) – это средний квадрат отклонений, получаемый путем деления суммы квадратов отклонений на число наблюдений (усреднение всех отклонений). Дисперсия меняется от нуля до бесконечности (выборочная дисперсия переменной X (термин впервые введен Фишером в 1918 г.) вычислялась по формуле:
где n – число наблюдений, d – отклонения вариант от среднего (x- Для определения дисперсии в простых вариационных рядах необходимо: найти отклонения вариант от средней арифметической d= (x- Во взвешенных рядах для определения дисперсии необходимо: вычислить среднее арифметическое взвешенное найти отклонения от среднего арифметического d=(x- Недостаток дисперсии заключается в несоответствии ее размерности и размерности отдельных единиц числового ряда. Если варианты, выражены, например, в килограммах, то дисперсия дает квадрат этой меры. Среднее квадратическое отклонение (от английского standart deviation) – корень квадратный из дисперсии: Для взвешенного вариационного ряда формула выглядит так:
Взаимоотношения среднего арифметического, среднего квадратического отклонения и отдельных вариант иногда называют правилом трех сигм. Коэффициент вариации (Cv) представляет процентное отношение среднего квадратического отклонении к среднему арифметическому: Cv = Коэффициент показывает разброс признака в нормированных границах: если его значение не превышает 10%, то можно говорить о слабом разбросе, если в пределах 10-20% - разброс средний, более 20% - имеет место большой разброс вариант. Квантиль (перцентель, персентиль; термин впервые использован Кендаллом в 1940 г.) выборки представляет число Квантили делят область возможных изменений вариант в вариационном ряду на определеннее интервалы. Формально p -квантиль непрерывного распределения F определяется как корень уравнения F (x) = p,0 < p <1. Квартили – значения, которые делят две половины выборки (разбитые медианой) еще раз пополам. Таким образом, медиана и квартили делят диапазон значений переменной на четыре равные части. Верхняя квартиль делит пополам верхнюю часть выборки (значения переменной больше медианы, символ 75%, означает, что 75% значений переменной меньше верхней квартили)), и нижнюю квартиль (символ 25%, означает, что 25% значений переменной меньше нижней квартили), которая меньше медианы и делит пополам нижнюю часть выборки. То есть, другими словами, 25-я процентиль переменной – это значение, ниже которого располагаются 25% значений переменной; 75-я процентиль равна значению, ниже которого расположено 75% значений переменной (¼ наблюдений лежит между минимальным значением и нижней квартилью, ¼ - между нижней квартилью и медианой, ¼ - между медианой и верхней квартилью, ¼ - между верхней квартилью и максимальным значением выборки). Квартильный размах переменных (термин впервые использован Галтоном в 1882 г.) равен разности значений 75-процентили и 25-й процентили. Таким образом, это интервал, содержащий медиану, в который попадает 50% наблюдений. Статистические моменты. Ассимметрия и эксцесс. Для вычисления этих показателей используется понятие момента генеральной совокупности. Различают моменты относительно начала отсчета и центральные моменты Формула относительно среднего параметра. для вычисления моментов: Асимметрия – или коэффициент асимметрии (термин введен Пирсоном в 1895 г.), является мерой несимметричности распределения. Если этот коэффициент значительно отличается от 0, то распределение является асимметричным (несимметричным). Формально имеем:
Эксцесс (или коэффициент эксцесса – термин впервые введен Пирсоном в 1905 г.) измеряет остроту пика распределения. Оценка эксцесса вычисляется по формуле:
где Асимметрия и эксцесс полезны для проверки нормальности данных. Нормальное распределение симметрично, следовательно, коэффициент асимметрии равен 0. Эксцесс нормального распределения также равен 0, поэтому по отклонениям выборочного эксцесса и асимметрии от 0 можно судить о близости распределения наблюдаемой переменной к нормальному. Известно, что распределение с более острой вершиной, чем нормальное, в типичных случаях имеет положительный эксцесс, а с более закругленной – отрицательный. Статистические гипотезы. Статистическая гипотеза должна быть сформулирована на этапе организации исследования. Выдвинутая гипотеза может быть правильной или неправильной и поэтому она проверяется на истинность с применением статистических методов. Р-уровень (статистическая значимость). Статистическая значимость результата представляет собой оцененную меру уверенности в его правильности. Этот уровень показывает, насколько значим для нас полученный результат. Например, проводя анализ здоровья на различных территориях мы используем комплексную систему обработки значений по отчетным формам и приходим к выводу, что на n… территории здоровье населения с большей вероятностью хуже, следовательно, полученный результат значим. Чем выше р-уровень (высокий уровень), тем меньше доверия к найденной в выборке зависимости между переменными. И, наоборот, чем ниже р-уровень, тем больше доверия. Пример: р-уровень = 0,05 (т.е. 1/20) показывает, что имеется 5%-я вероятность того, что найденная в выборке зависимость между переменными является лишь случайной особенностью данной выборки. Этот уровень во многих исследованиях рассматривается, как «приемлемая граница» уровня ошибки (в жизни это – при многократном проведении эксперимента может или не получится результата, или он может получится в 1 случае из 20 повторений эксперимента). С другой стороны, мы выдвигаем гипотезу о том, что данная территория. К примеру, экологически благополучная. Если мы получили р-уровень 0,05, то в среднем в 5 случаях их 100 (изучаемых территорий) мы будем совершать ошибку (т.е. принимать неправильную гипотезу – признавать территорию экологически благополучной, когда на самом деле она экологически неблагополучная). Таким образом, выбор уровня значимости (таблица № 7), выше которого результаты отвергаются как ложные, является достаточно произвольным. На практике окончательное решение обычно зависит от того, был ли результат априори (т.е. до есть до проведения опыта) или обнаружен апостериорно - в результате проведения многих анализов с множеством данных, а также по традиции, имеющейся в области исследований. Таким образом, в СГМ при комплексном изучении здоровья результат получается апостериорно – с применением многих методов по знакомым апробированным методикам. Таблица № 7
|
||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 3064; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.73.167 (0.009 с.) |

 и читается «Х с чертой». Формула расчета:
и читается «Х с чертой». Формула расчета: .
.
 =0.
=0.
 называется вариационным рядом, а ее элементы – порядковыми статистиками. Если число наблюдений нечетно n=2m+1, то медиана оценивается как
называется вариационным рядом, а ее элементы – порядковыми статистиками. Если число наблюдений нечетно n=2m+1, то медиана оценивается как  .
. +
+  )/2.
)/2. =
=  ,
, ).
). = (x-
= (x-  , суммировать полученные квадраты отклонений
, суммировать полученные квадраты отклонений  ; разделить сумму на число наблюдений
; разделить сумму на число наблюдений  .
. =
=  ,
, .
. =
=  или
или 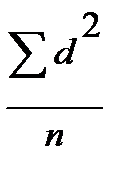 .
. %.
%. , ниже которого находится p -я часть (доли) выборки. Квантиль 0,25 для некоторой переменной – это такое значение (
, ниже которого находится p -я часть (доли) выборки. Квантиль 0,25 для некоторой переменной – это такое значение ( =
=  , где
, где 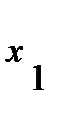 - наблюдаемые варианты, p – их частоты, n – число наблюдений, k – степень (порядок) момента, С – произвольное постоянное число.
- наблюдаемые варианты, p – их частоты, n – число наблюдений, k – степень (порядок) момента, С – произвольное постоянное число. .
. =
= 
 =
=  .
.


