
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические методы выявления систематической погрешности
Выявить отсутствие или наличие систематической (и не только систематической) погрешности на стадии анализа результатов помогают специальные статистические методы. В каждом из этих методов используется определенный критерий (обозначим его в общем случае символом φ). При этом могут возникнуть следующие ошибки. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Будем далее рассматривать ошибки первого рода. Вероятность q такой ошибки называется уровнем значимости. Соответственно, вероятность P принятия правильной гипотезы называется доверительной вероятностью, при этом q = 1 ‑ Р. Признаком правильности принятой гипотезы является попадание критерия φ в интервал значений, определяемый доверительной вероятностью Р. За границами этого интервала находится область значений критерия φ, когда предложенная гипотеза отвергается. Положение границы между этими областями – φкр зависит от вида критерия φ, а также доверительной вероятности Р и числа измерений n. Как правило, значения φкр для разных методов сведены в таблицы (см. приложение). Заметим, что если признаком правильности выбранной гипотезы является неравенство φ < φкр,то с увеличением доверительной вероятности Р величина φкр уменьшается. Если же признаком правильности выбранной гипотезы является неравенство φ > φкр,то с увеличением доверительной вероятности Р величина φкр также увеличивается. Таким образом, чем больше доверительная вероятность, тем строже должно быть неравенство. Рассмотрим следующие статистические методы. а) Способ последовательных разностей (критерий Аббе) – для обнаружения изменяющейся во времени систематической погрешности (при числе измерений до 20). Пусть имеется выборка из n измерений Х1, Х2, …Хn некоторого параметра Х и среднее его значение Определяют дисперсию выборки по формуле:
Кроме того, вычисляют функцию суммы квадратов разности соседних по времени измерений по формуле:
Если со временем происходило смещение центра группирования измерений, т.е. имела место переменная систематическая погрешность, очевидно, величина s2(Х) дает преувеличенную оценку дисперсии.
Действительно, допустим, что среднее значение В этом случае истинный разброс величины Х в каждый момент времени следовало бы оценивать относительно текущего среднего значения В то же время на величину Q2(Х) дрейф средней величины сказывается незначительно, поскольку мы оперируем с соседними по времени измерениями. Отношение n= Q2(Х) / s2 (Х) и есть критерий обнаружения систематической, изменяющейся во времени погрешности (так называемый критерий Аббе). Чем меньше n, тем более вероятно наличие систематической погрешности. Попадание значения n в критическую область (n<nкр) означает наличие систематической погрешности. Определены табличные критические значения nкр для разных уровней значимости q и числа измерений n. Чем меньше значение q и, соответственно, больше P, т.е. чем выше должна быть наша уверенность, что переменная систематическая погрешность присутствует, а также чем меньше выполнено измерений, тем ниже должна опускаться планка критического значения nкр. Таблица критических значений (nкр) приводится в приложении (табл. 3). Примеры: 1. Измерения напряжений Х в балке мостового пролетного строения от одной и той же нагрузки, проводимые с помощью деформометра в течение некоторого времени, дали следующие результаты (МПа): 30 31 29 32 31 33 (всего 6 измерений). Требуется определить, имела ли место в этом случае систематическая погрешность. Среднее арифметическое - Дисперсия - s2 (Х) =2,0. Величина Q 2 (Х) =1,9.
Для всех табличных уровней значимости n > nкр., что означает отсутствие систематической погрешности.
2. Имеется ряд результатов измерения параметра Х: 30 30 31 32 34 35 Требуется выяснить наличие систематической погрешности. Статистическая обработка данных дает следующие результаты:
Зададимся двумя значениями уровня значимости и найдем по таблице соответствующие критерии:
q = 0.05; nкр= 0.445. q = 0.01; nкр= 0.281. Это означает, что при уровне значимости q =0,05 (nкр=0,445), т.е. с вероятностью 0,95 можно утверждать, что присутствует систематическая погрешность, но с вероятностью 0,99 (nкр=0,281) этого утверждать нельзя. б) Способ дисперсионного анализа (критерий Фишера) В практике измерений часто бывает необходимо проверить наличие систематической погрешности вследствие влияния какого-либо фактора. Например, при проведении испытаний мостов в процессе работы погодные условия могут меняться, и это отражается на результатах измерений. Для выявления систематической погрешности весь массив измерений разбивают на группы по принципу различного влияния исследуемого фактора. Например, при проведении измерений некоторого параметра для выяснения, влияет ли на них температура воздуха, можно выделить в отдельные группы утренние, дневные, ночные измерения. Пусть мы имеем всего n измерений, разбитых на s групп, и ni измерений в i -ой группе. В каждой группе должно иметь место нормальное распределение результатов измерений. Это означает, что разброс результатов в каждой группе обусловлен лишь случайными погрешностями. Определим для каждой группы среднее арифметическое и дисперсию. Совокупная характеристика случайных погрешностей в группах может быть выражена средним арифметическим значением дисперсий Di, определенных для каждой группы. Эта величина называется внутригрупповой дисперсией DВГ. Если число измерений в каждой группе одинаково, т.е. ni = n /s, можно записать:
где Хi,j – результат j-го измерения в i- ой группе. Поскольку группы подобраны таким образом, что в каждой из них дисперсия результатов определяется только случайными причинами, то и величина DВГ, очевидно, отражает только эти случайные причины (случайные погрешности). Рассеивание средних DМГ = где Графическое представление разбиения массива на группы и определения межгрупповой и внутригрупповой дисперсий приводится ниже на примере (рис.3.3). Отношение F= DМГ/DВГ выражает соотношение влияния на разброс систематической и случайной погрешности. Величину F называют дисперсионным критерием Фишера. По аналогии с критерием Аббе определены границы критических областей для критерия Фишера (Fкр) при различных значениях Р доверительной вероятности, массива результатов n, числа групп s (табл.2 приложения). Если вычисленное для данного массива измерений значение F при заданных n, q = 1 - Р, s больше соответствующего табличного значения Fкр, то гипотеза о систематической погрешности принимается.
Рис 3.3. Разбиение массива на однородные группы для определения критерия Фишера Пример. В течение суток в разное время проведено 30 измерений провиса металлического пролетного строения, в том числе по 10 измерений – в 5 часов, 12 часов и 19 часов.
Внутригрупповая дисперсия составила 0,05 см2; Межгрупповая дисперсия – 0,2 см2. Выявить, была ли систематическая погрешность, вызванная разным нагревом конструкции на протяжении суток. Расчетное значение критерия Фишера F= 0,2/0,05 =4. K 1= s -1=2; K 2= n-s =28; Табличное значение критерия Фишера: для уровня значимости q =0,05 Fq =3,37; для q =0,01 Fq =5,53. Таким образом, в первом случае, т.е. с вероятностью 0,95, можно говорить о систематической погрешности, а во втором, т.е. с вероятностью 0,99, этого сказать нельзя. Исправление выявленных систематических погрешностей при обработке результатов может быть выполнено путем введения поправок, нейтрализующих влияние факторов, вызывающих погрешность.
Контрольные вопросы: 1. Что такое систематическая погрешность? 2. Назовите условия уменьшения возможности появления систематической погрешности. 3. Можно ли устранить систематическую погрешность многократными измерениями? 4. Назовите известные Вам способы устранения систематической погрешности статистическими методами. 5. Объясните существо способа последовательных разностей (критерий Аббе). 6. Объясните существо способа дисперсионного анализа (критерий Фишера).
Случайные погрешности Случайная погрешность – это составляющая погрешности измерения, которая изменяется случайным образом в серии повторных измерений одного и того же размера физической величины, проведенных с одинаковой тщательностью в одних и тех же условиях. Случайные погрешности неизбежны, неустранимы и их можно описать и ограничить только приемами математической статистики. При этом необходимо решить две задачи: - установить закон распределения вероятностей случайной погрешности и убедиться, что массив измерений соответствует этому закону; - получить интервальную оценку истинного значения измеряемой физической величины. Применительно к исследованию свойств строительных материалов и конструкций можно утверждать, что в большинстве случаев случайные погрешности имеют вероятностную основу, подчиняющуюся нормальному закону распределения, который описывает случайные величины, зависящие от многих незначительных случайных факторов. Поэтому в настоящем курсе мы ограничимся рассмотрением именно этого распределения. Познакомиться с другими законами распределения читатель может в специальной литературе по теории вероятностей, математической статистики, теоретической метрологии.
Итак, нормальным называется распределение вероятностей случайной величины х, подчиняющееся закону: плотность распределения:
функция распределения:
Математическое ожидание M(x) при этом равно α: среднеквадратическое отклонение (стандарт) – s. Как видно из приведенных формул, нормальное распределение симметрично относительно математического ожидания. Путем замены переменных t = (x-a) /s это распределение можно привести к нормированного виду, для которого M (t) =0 и s (t) =1, т.е.:
Для плотности и функции нормированного нормального распределения составлены таблицы (табл. 1 и 2 приложения).
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 2405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.239.148 (0.039 с.) |
 .
. . (3.3)
. (3.3) . (3.4)
. (3.4) измеряемой величины Х дрейфует со временем, принимая текущие значения
измеряемой величины Х дрейфует со временем, принимая текущие значения  , т.е. присутствует систематическая погрешность.
, т.е. присутствует систематическая погрешность. =31.
=31. .
. .
. , (3.5)
, (3.5)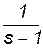
 (
(
 ; (4.1)
; (4.1) . (4.2)
. (4.2) ; (4.1’)
; (4.1’) - (функция Лапласа). (4.2’)
- (функция Лапласа). (4.2’)


