
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Погрешности измерений и средств измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Погрешности измерений Отклонение результата измерения от истинного значения измеряемой величины называется погрешностью измерения. Различают абсолютные погрешности измерения, которые выражаются в единицах измеряемой величины, и относительные погрешности измерения, определяемые как отношение абсолютной погрешности измерения к значению измеряемой величины: Δ = х – хи; (3.1) δ = Δ/х, (3.2)
где Δ - абсолютная погрешность измерения; х - значение, полученное при измерении; хи - истинное значение измеряемой величины; δ - относительная погрешность измерения. Абсолютная погрешность Δ является результирующей погрешностью, т.е. суммой систематической Δс и случайной Δ0 погрешностей. Систематической погрешностью измерения называется составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины (неисправности измерительной аппаратуры, несовершенство метода измерений, неправильная установка измерительных приборов и т.д.). Случайной погрешностью измерения называется составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельности мало влияет на результат измерения. Результат измерения, содержащий грубую погрешность (промах), следует выявить, исключить и не учитывать при дальнейшей статистической обработке. Существуют некоторые общие причины возникновения систематических погрешностей, в соответствии с которыми их подразделяют на методические, инструментальные и субъективные. Методические погрешности происходят от несовершенства метода измерения, использования упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения. Например, измерение температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима исследуемого объекта (вследствие внесения термопары). Инструментальные погрешности зависят от погрешностей применяемых средств измерения. Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуатации и т.д. являются причинами инструментальных погрешностей. Субъективные погрешности вызываются неправильными отсчетами показаний прибора оператором. Систематические погрешности могут оставаться постоянными либо закономерно изменяться. В последнем случае их подразделяют на прогрессирующие (возрастающие или убывающие), периодические и изменяющиеся по сложному закону. Обнаружение причин и источников систематических погрешностей позволяет принять меры к их устранению или исключению посредством введения поправки. Поправкой называется значение величины, одноименной с измеряемой, которое нужно прибавить к полученному при измерении значению величины с целью исключения систематической погрешности. В некоторых случаях используют поправочный множитель - число, на которое умножают результат измерения для исключения систематической погрешности. Согласно теория вероятностей случайная величина наиболее полно характеризуется своим законом распределения (или плотностью распределения) вероятностей. При измерении чаще всего встречается нормальная и равномерная плотность распределения случайной величины.
Рисунок 3.1 – Нормальный закон распределения погрешностей Нормальный закон распределения вероятностей имеет вид
где Кривые, соответствующие выражению (3.3) для разных значений σ, приведены на (рис.3.1). Очевидно, что при малых значениях σ получается погрешность измерений меньше, чем при больших. Вероятность того, что погрешность результата измерения находится между заданными предельными значениями
Интеграл в формуле (3.4) вычисляется по таблицам функции Лапласа Ф(z). Распределение погрешностей принимают равномерным, если
Такой закон распределения характерен, например, для погрешностей отсчета по шкале прибора, погрешностей дискретности в цифровых измерительных приборах, погрешностей квантования в аналого-цифровых преобразователях (АЦП). Поскольку истинное значение измеряемой величины хи неизвестно, непосредственно случайную абсолютную погрешность Δ вычислить нельзя. При практических расчетах приходится вместо хи использовать его оценку. Обычно принимают, что истинное значение равно среднему арифметическому значению ряда измерений:
где xi - результаты отдельных измерений; n - число измерений.
Вероятность Рд называется доверительной вероятностью, а интервал значений измеряемой величины от х – Δ до х + Δ - доверительным интервалом. Приведенное выше равенство означает, что с вероятностью Рд доверительный интервал от х - Δ до х + Δ заключает в себе истинное значение хи. Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами - доверительной вероятностью и соответствующим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 967; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.1 (0.006 с.) |


 (3.3)
(3.3)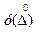 - плотность вероятностей случайной погрешности
- плотность вероятностей случайной погрешности  ; σ -среднее квадратическое значение случайной погрешности.
; σ -среднее квадратическое значение случайной погрешности. и
и  вычисляется по формуле:
вычисляется по формуле: (3.4)
(3.4) (3.5)
(3.5)
 Введем важные понятия доверительной вероятности и доверительного интервала. Среднее арифметическое значение
Введем важные понятия доверительной вероятности и доверительного интервала. Среднее арифметическое значение  , полученное в результате некоторого ряда измерений, является оценкой истинного значения хи и, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть Рд есть вероятность того, что
, полученное в результате некоторого ряда измерений, является оценкой истинного значения хи и, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть Рд есть вероятность того, что  отличается от хи не более чем на Δ, т.е.
отличается от хи не более чем на Δ, т.е. (3.6)
(3.6)


