
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Измерение напряжений и токовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основные значения измеряемых напряжений и токов
На практике часто измеряют напряжения, несколько реже - токи. Это объясняется тем, что для измерения тока измеряемую цепь необходимо разрывать, что не всегда возможно или желательно. Измеряемые электрические сигналы (токи или напряжения) представляют собой, как правило, сложные функции времени. Поэтому для анализа и сравнения различных сигналов стремятся использовать такие их значения, которые характеризовали бы сигналы любой формы. Наиболее распространенными являются следующие значения (параметры) напряжений и токов: амплитудное, среднее, средневыпрямленное и среднеквадратическое. Рассмотрим суть этих значений применительно к напряжению. Амплитудное (пиковое) значение представляет собой наибольшее или наименьшее мгновенное значение переменной составляющей сигнала за время измерения
где В общем случае положительные и отрицательные пиковые значения переменного напряжения могут быть различными. Среднее значение (постоянная составляющая) напряжения определяется выражением
где Т1 - время наблюдения или период электрического колебания; Т2 - время действия измеряемого напряжения. Интервалы Т1 и Т2 не всегда равны друг другу. При измерении среднего значения импульсных напряжений время действия измеряемого напряжения меньше периода электрического колебания (Т2 < Т1). По физическому смыслу Uсp - это постоянная составляющая сигнала U(t) за время Т1, а графически — это высота прямоугольника с основанием Т1, площадь которого равна площади, определяемой функцией U{t) и осью времени за один. Средневыпрямленное значение напряжения
Графически Uсв - это высота прямоугольника с основанием Т1, площадь которого равна площади, определяемой функцией U(t) над и под осью времени. При таком определении считается, что операция нахождения средневыпрямленного значения осуществляется с помощью двух полупериодного детектора средневыпрямленных значений. Заметим, что для однополярных сигналов Uсp и Uсв равны между собой. Среднеквадратическое значение напряжения - это корень квадратный из среднего значения квадрата напряжения:
Среднеквадратическое значение периодического сигнала сложной формы может определяться также как сумма квадратов постоянной составляющей и среднеквадратических значений отдельных гармоник, т.е.
Постоянную составляющую U0 и гармоники U1,U2,…Un находят путем разложения сложной функции времени U{t) в ряд Фурье. Пиковое, среднеквадратическое и средневыпрямленное значения напряжений сигналов любой формы связаны между собой коэффициентами амплитуды Ка, формы Kф и усреднения Kу:
Конкретные значения Ка и Кф зависят от формы сигналов и вычисляются с использованием формул (4.2), (4.3) и (4.4). Например, основные соотношения между значениями для синусоидального сигнала U(t) = Umsinωt будут равны:
Вычисление различных значений переменного напряжения По показаниям вольтметров
Большинство электронных вольтметров, предназначенных для измерения переменных напряжений, градуируют в среднеквадратических значениях синусоидального напряжения (за исключением импульсных вольтметров, которые градуируют обычно по амплитудному значению). Следовательно, показания таких приборов соответствуют среднеквадратическим значениям синусоидальных сигналов. А как определить максимальное или средневыпрямленное значение напряжения гармонического или более сложного сигнала? Для этого необходимо знать градуировочную характеристику приборов, которая устанавливает соотношение между показанием прибора Ап и значением измеренного напряжения Ап = φ[U{t)]. В общем виде для приборов с закрытым для постоянной составляющей сигнала входом градуировочную характеристику можно представить в следующем виде:
где С - градуировочный коэффициент, зависящий от вида преобразователя; φ - функциональные преобразования вида (4.1)-(4.5); Uпc - постоянная составляющая измеряемого сигнала. Для приборов с открытым входом
Рассмотрим процесс градуировки с помощью схемы на (рис.4.1), где параллельно включены три прибора, имеющие преобразователь пиковых значений (ППЗ), преобразователь средневыпрямленных значений (ПСВЗ) и преобразователь среднеквадратических значений (ПСКЗ). Шкалы всех вольтметров среднеквадратические.
Рисунок 4.1 Схема градуировки вольтметра При одном и том же значении входного гармонического сигнала показания вольтметров будут отсчитаны в среднеквадратических значениях, в соответствии с (4.8), т.е. можно записать
С учетом (4.6) градуировочные характеристики запишутся в следующем виде:
Таким образом, при проведенной градуировке, когда шкалы всех приборов градуированы с СКЗ синусоидального напряжения, по. показаниям приборов могут быть определены все остальные параметры синусоидального сигнала через коэффициенты амплитуды и формы, независимо от типа преобразователя, используемого в данном вольтметре:
Представим, что на три вольтметра вместо гармонического сигнала подается сигнал Ux(t) сложной формы. В этом случае по аналогии с (4.10) показания приборов запишутся в следующем виде:
Очевидно, что Kaх ≠ Кasin и Кфх ≠ Кфsin, поэтому показания Ап1 и Ап2 приборов, проградуированных синусоидальным сигналом, не будут соответствовать параметрам измеряемого сложного сигнала. Показание третьего прибора Ап3, проградуированного в значениях параметра, на который реагирует его преобразователь (С = 1), будет соответствовать значению измеряемого сигнала, т.е. показания этого вольтметра не зависят от формы измеряемого напряжения. Таким образом, при измерении сложного сигнала вольтметрами, проградуированными гармоническим сигналом в значениях, отличных от значений, на которые реагирует преобразователь, имеет место систематическая погрешность, величина которой будет тем больше, чем больше Ках и Кфх будут отличаться от Кasin и Кфsin. Следовательно, в этом случае при измерении несинусоидального напряжения показания приборов должны быть переоценены, т.е. внесены поправки в соответствии со значениями Ках и Кфх измеряемого сигнала. При внесении поправок в первую очередь следует, используя Кasin или Кфsin, определить значение напряжения, на которое реагирует преобразователь, а затем другие значения напряжений. Например, при использовании вольтметра с пиковым преобразователем и среднеквадратической шкалой непосредственно по показанию прибора первоначально находится
а затем
Если вольтметр имеет закрытый вход, то измеряемое напряжение сложной формы следует представить как сумму двух напряжений: постоянного (Uпс), равного среднему значению, и переменного (U~) с нулевым средним значением (рис.4.2) и при определении значений различных параметров напряжений следует воспользоваться градуировочной характеристикой (4.7).
Рисунок 4.2 – Представление пилообразного напряжения в виде двух составляющих Пример. С помощью милливольтметра с закрытым входом измеряется цифровой сигнал (импульсная последовательность амплитудой Um, длительность импульсов tи, период следования Т). Прибор имеет преобразователь пиковых значений и среднеквадратическую шкалу. Показание прибора Ап = 50 мВ. Определить амплитудное (Um), среднеквадратическое {Uск) и средневыпрямленное (Ucв) значения измеряемого напряжения. Учитывая (4.7) и (4.6), запишем
Для прямоугольных импульсов справедливо. что
Следовательно,
Учитывая, что
Учитывая, что
При Q = 2 имеем Um = 141 мВ; Ucк = 99,4 мВ; Uсв = 70,5 мВ.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.011 с.) |

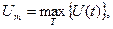 (4.1)
(4.1) - операция нахождения максимального значения сигнала U(t) на интервале измерения Т.
- операция нахождения максимального значения сигнала U(t) на интервале измерения Т.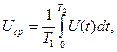 (4.2)
(4.2)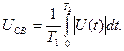 (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5) (4.6)
(4.6)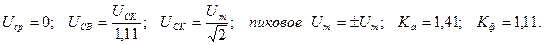
 (4.7)
(4.7)
 (4.8)
(4.8)
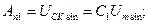
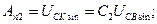 (4.9)
(4.9)
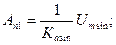
 (4.10)
(4.10)

 (4.11)
(4.11)

 (4.12)
(4.12)
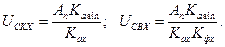 (4.13)
(4.13)

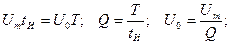

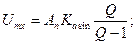
 получим
получим
 получим
получим



