
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погрешности средств измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Входной величиной измерительного прибора является его измеряемая величина. Наибольшее и наименьшее значения измеряемой величины, для которых нормированы погрешности, называются пределами измерения. Область значений, заключенная между верхним и нижним пределами измерения, называется диапазоном измерений. От диапазона измерений следует отличать диапазон показаний, который охватывает область значений шкалы, ограниченную конечным и начальным значениями шкалы. Таким образом, диапазон измерений, охватывающий часть шкалы, в пределах которой измерения могут быть проведены с нормируемой погрешностью, более узок, чем диапазон показаний, охватывающий всю шкалу. Функция преобразования - функциональная зависимость между выходной величиной у и входной величиной х. Желательно, чтобы функция преобразования была линейной. Чувствительность - это отношение изменения выходной величины измерительного прибора к вызвавшему ее изменению входной величины S = dy/dx. (3.7) Для прибора или преобразователя может определяться абсолютная, относительная и приведенная погрешности. Абсолютная погрешность прибора в данной точке диапазона измерения равна Δ = хп - х, (3.8) где хп - показание прибора; х - истинное значение измеряемой величины. Однако в связи с тем, что истинное значение неизвестно, на практике вместо него используется действительное значение хд. В качестве хд принимают показания более точного, образцового прибора. Относительная погрешность прибора равна отношению абсолютной погрешности к истинному значению измеряемой величины и обычно выражается в процентах: δ = (Δ/х) • 100 = [(xп - х)/х] 100. (3.9) Приведенная погрешность прибора у также выражается в процентах и равна отношению абсолютной погрешности к нормирующему значению xN, которое принимается равным верхнему пределу измерений (если нулевая отметка находится на краю или вне шкалы) или диапазону измерения (если нулевая отметка находится внутри диапазона измерений): γ = (Δ/xN) ∙ 100 = [(хП - x)/xN] 100. (3.10) Значения абсолютной, относительной и приведенной погрешностей используются для нормирования погрешности приборов. Обычно СИ имеют линейную функцию преобразования у = S ∙ x + у0, (3.11) где S – чувствительность прибора; у0 - значение выходной величины при нулевом значении входной. Отклонение такой функции преобразования от номинальной может быть вызвано отклонением у0 и отклонением чувствительности S. Погрешность, обусловленная неноминальным значением выходной величины при нулевом значении входной у0, называется аддитивной. Погрешность, обусловленная неноминальным значением чувствительности S, называется мультипликативной. Аддитивная погрешность не зависит от входной величины. При изменении у0 вследствие каких-либо причин график функции преобразования перемещается параллельно самому себе (рис.3.2,а). Значение этой погрешности Δу = Δу0 = у0 - у0ном , (3.12) где у0ном — номинальное значение у0. При мультипликативной погрешности наклон прямой, графически отображающий функцию преобразования, отличается от наклона при номинальной функции преобразования (рис.3.1,б). При этом абсолютная погрешность Δу = у- уномзависит от входной величины х. При изменении чувствительности на ΔS абсолютная погрешность преобразователя Δу = ΔS ∙ х, (3.13) т.е. абсолютная мультипликативная погрешность пропорциональна входной величине х.
а) б) Рисунок 3.2 – Погрешности: а) аддитивная; б) мультипликативная Относительная мультипликативная погрешность равна δ у = ΔS/S (3.14) Относительная мультипликативная погрешность равна относительному изменению чувствительности. Погрешность СИ зависит от условий проведения измерений. При этом различают основную и дополнительную погрешности. Основной погрешностью называется погрешность, существующая при так называемых нормальных условиях, которые указаны в нормативных документах, регламентирующих правила испытания и эксплуатации данного средства измерения. Например, нормальные условия считаются когда температура окружающей среды +20 ± 2°С; положение прибора горизонтальное с отклонением < ± 2°; относительная влажность 65 ± 15%; отсутствие магнитных и электрических полей; частота питающей сети 50 ± 1 Гц и т.д. Дополнительная погрешность возникает при отклонении условий испытания и эксплуатации средства измерения от нормальных. Например, приведенная погрешность прибора при нормальных условиях, т.е. в диапазоне температур (+20 ± 2)°С, не превышает 1%. Если температура лежит вне указанного диапазона, то погрешность может быть больше указанной. Класс точности - это обобщенная метрологическая характеристика, определяемая пределами допускаемых основной и дополнительных погрешностей, значения которых устанавливаются в стандартах на отдельные виды средств измерения. Класс точности стрелочных и самопишущих приборов обозначается одним числом с, равным максимально допускаемому значению приведенной погрешности
Класс точности цифровых приборов указывается в виде дроби c/d, по которой определяется относительная погрешность
где хк – верхний предел измерения. Значения c,d выбирают из следующего ряда:
Порог чувствительности - это изменение измеряемой величины, вызывающее наименьшее изменение показаний, различимое при нормальном для данного прибора способе отсчета. Собственное потребление мощности прибором из цепи, в которой производится измерение, является важной характеристикой прибора. Особенно сильно это проявляется при измерениях в маломощных цепях. Описанные выше характеристики являются статическими, т.е. не зависящими от времени. Они имеют смысл только в том случае, если параметры измерительного прибора и значение измеряемой величины остаются постоянными, а время измерения не ограничено. Однако измеряемая величина меняется по времени, измерение проводится за короткое время, параметры измерительного прибора изменяются и т.д.. Одновременный учет всех этих особенностей процесса измерения затруднителен. Поэтому предполагается, что средство измерения является линейной системой, т.е. может быть характеризовано линейным дифференциальным уравнением с постоянными коэффициентами: a0d ny/dt n + a1d n-1y/dt n-1 +…+any = x(t), где а0, a1,..., аn — постоянные коэффициенты. При нулевых начальных условиях уравнение в операторной форме имеет вид (а0рn + a1p n-1 + …+ an)y(p) = x(p), где p = d/dt – оператор дифференцирования. Передаточной функцией СИ называется отношение изображений по Лапласу выходной величины к входной: W(р) = у(р)/х(р). (3.17) Зная передаточную функцию преобразователя, можно определить его реакцию y(t) на заданное изменение измеряемой величины x(t) и определить динамическую погрешность Δу(t) = y{t) – уст, (3.18) где y(t) - значение выходной величины СИ в момент времени t; уст - значение выходной величины, заданное его статической функцией преобразования. При анализе динамических характеристик используются типовые входные воздействия: единичная и гармоническая функции. Если в (3.17) подставить вместо р = jω, то можно определить частотную передаточную функцию СИ
где А(ω) - модуль частотной передаточной функции; φ(ω) - сдвиг фаз между входной и выходной величинами. Зависимость модуля частотной передаточной функции от частоты А(ω) определяет амплитудно-частотную характеристику (АЧХ); зависимость ее аргумента от частоты φ(ω) определяет фазочастотную характеристику (ФЧХ). К важным динамическим характеристикам приборов относится время установления показаний - промежуток времени, прошедший с момента подключения или изменения измеряемой величины до момента, когда отклонение указателя от установившегося значения не превышает 1,5% длины шкалы. Для цифровых приборов указывается время измерения, отсчитываемое от начала измерения до получения результата на отсчетном устройстве с нормированной погрешностью. Надежность прибора - способность сохранять заданные характеристики при определенных условиях в течение заданного времени. Выход значения параметров и характеристик прибора за пределы нормы считается отказом. Отказ измерительного прибора может наступить, если его действительная погрешность станет больше ее нормирующего значения, определяемого классом точности. Количественным показателем надежности является наработка на отказ - среднее время безотказной работы прибора. Наработка на отказ является статистической величиной. Она устанавливается для данной серии приборов на основании выборочных испытаний небольшой партии, входящих в эту серию.
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |


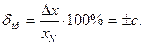 (3.15)
(3.15) (3.16)
(3.16)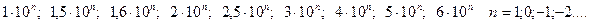
 (3.19)
(3.19)


