
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка косвенных видов измеренийСодержание книги
Поиск на нашем сайте
При косвенных видах измерений значение искомой величины Y получают на основании прямых видов измерений величин xi, связанных с измеряемой известной функциональной зависимостью: Y = f(X1, X2, X3, …, Xm), где Xi –подлежащие прямым измерениям аргументы функции искомой величины Y. Проводим обработку косвенных видов измерений. Уравнение связи имеет вид: Результаты измерений аргументов X1 и X2 представлены в таблице 2.1. Таблица 2.1 – Результаты измерений аргументов X1 и X2
1) На основании формул (1.5) и (1.8) раздела 1.1 проводим точечную оценку каждого аргумента, т. е. находим значения X̅i и Sx̅i. X̅1 = 20,41; Sx̅1 = 0,01, X̅2 = 4,88; Sx̅2 = 0,08. 2) Исходя из уравнения связи (2.1) оцениваем искомый результат:
где X̅1 – среднее значение результатов измерений первой серии, X̅2 – среднее значение результатов измерений второй серии.
3) Находим коэффициенты влияния
4) Находим коэффициент корреляции между парой аргументов по формуле (2.7) r= где – h=min(n1;n2) – наименьшее из чисел наблюдений n1 и n2 соответственно аргументов x1 и x2. r = 0,325. 5)
6)
Kэф=23. 7) Коэффициент Стьюдента определили по таблице 4 при pд=0,95, который равен 2,069. 8) Оценка погрешности Y = 99,65 ± 0,24 при pд = 0,95. Задание 2 По известной расчетной зависимости косвенного метода измерения (искомый результат) и по известным результатам и погрешностям прямых измерений получить формулу и среднеквадратическую оценку погрешности косвенного измерения δyск. Исходные данные для расчёта: y =0,5/[(a+b)(c-d)e2], Δa = 3; a = 100, Δb = 1; b = 70, Δc = 2; c = 80, Δd = 1; d = 60, Δe = 2; e = 90. Прологарифмируем левую и правую части заданной зависимости: lny = ln(0,5)-ln(a+b)-ln(c-d)-2ln(e). Найдём дифференциал правой и левой частей dlny = dln(0,5)- dln(a+b)-dln(c-d)-2dln(e). С учётом того, что dln(0,5) = 0, получим dlny = - dln(a+b)-dln(c-d)-2dln(e). Учитывая, что дифференциал от логарифма переменной величины находится по формуле d(ln x) =
Произведём широко используемую в теории погрешностей замену дифференциалов малыми абсолютными погрешностями (при условии, что абсолютные погрешности достаточно малы), т.е. dy ≈ Δy, d(a+b) ≈ Δ(a+b), d(c) ≈ Δc, d(d-e) ≈ Δ(d-e).
Находим предельную оценку абсолютной погрешности косвенного измерения:
Найдём среднеквадратическую оценку относительной погрешности косвенного измерения y
Нормирование метрологических характеристик средств измерений классами точности
Задание 1
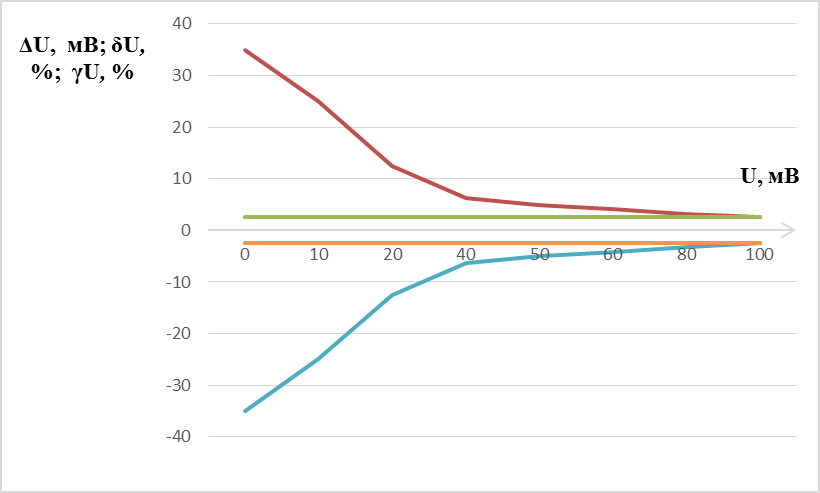
Милливольтметром класса точности 2,5 со шкалой (0…100) мВ измерены значения напряжения 0; 10; 20; 40; 50; 60; 80; 100 мВ. Рассчитать зависимости абсолютной, относительной и приведённой основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков. Для записи результатов формируем таблицу 3.1, в столбцы которой будем записывать измеренные значения U, абсолютные Δ U, относительные δ U и приведённые γ U погрешности. В первый столбец записываем заданные в условии задачи измеренные значения напряжения: 0; 10; 20; 40; 50; 60; 80; 100 мВ. Класс точности милливольтметра задан числом без кружка, следовательно, приведённая погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т. е. |γ U | ≤ 2,5 %. При решении задачи рассмотрим худший случай |γ U| = 2,5 %, когда приведённая погрешность принимает максимальное по абсолютной величине значение, что соответствует γ U = +2,5 % и γ U = –2,5 %. Данные значения приведённой погрешности заносим в четвёртый столбец таблицы 3.1. Таблица 3.1 – Результаты расчёта значений погрешностей
Продолжение таблицы 3.1
Рассчитаем значения абсолютной погрешности. Из формулы милливольтметра содержит нулевую отметку, т.е. UN = |100 мВ – 0 мВ| = 100 мВ. Абсолютная погрешность Значения относительной погрешности будем рассчитывать по формуле
При U = 0 мВ получаем При U = 10 мВ получаем При U = 20 мВ получаем При U = 40 мВ получаем При U = 50 мВ получаем При U = 60 мВ получаем При U = 80 мВ получаем При U = 100 мВ получаем Полученные таким образом значения относительной погрешности заносим в третий столбец. По данным таблицы 3.1, учитывая, что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной Δ U, относительной δ U и приведённой γ U погрешностей от результата измерений U (рисунок 3.1).
Рисунок 3.1 – Графики зависимостей абсолютной, относительной и приведённой погрешностей от результата измерений для прибора с преобладающими аддитивными погрешностями.
Задание 2 Термометром класса точности 0,1 со шкалой (0…250) °С измерены значения температуры 0; 25; 50; 100; 125; 150; 200; 250 °С. Рассчитать зависимости абсолютной и относительной погрешностей от результата измерений. Результаты представить в виде таблицы и графиков. Для записи результатов формируем таблицу 3.2, в столбцы которой будем записывать измеренные значения t, абсолютные Δ t и относительные δ t погрешности. Таблица 3.2 – Результаты расчёта значений погрешностей
Продолжение таблицы 3.2
В первый столбец записываем заданные в условии задачи измеренные значения температуры: 0; 25; 50; 100; 125; 150; 200; 250 °С. Класс точности термометра задан числом в кружке, следовательно, относительная погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е. |γt| ≤ 0,1%. При решении задачи рассмотрим худший случай, т.е. |γt| = 0,1%, что соответствует значениям γt = +0,1% и γt = -0,1%. Примем во внимание опыт решения задачи 1, из которого видно, что результаты вычисления, выполненные для положительных и отрицательных значений погрешностей, численно совпадают друг с другом и отличаются только знаками «+» или «−». Поэтому дальнейшие вычисления будем производить только для положительных значений относительной погрешности γt = 0,1%, но при этом будем помнить, что все значения второго и третьего столбцов таблицы 3.2 могут принимать и отрицательные значения. Значение относительной погрешности γt = 0,1 % заносим в третий столбец таблицы. Рассчитаем значения абсолютной погрешности. Из формулы
При t = 0 °С получаем При t = 25 °С получаем При t = 50 °С получаем При t = 100 °С получаем При t = 125 °С получаем При t = 150 °С получаем При t = 200 °С получаем При t = 250 °С получаем Полученные таким образом значения абсолютной погрешности заносим во второй столбец. По данным таблицы 3.2, учитывая, что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной Δ t и относительной δ t погрешностей от результата измерений t (рисунок 3.2).
Рисунок 3.2 – Графики зависимостей абсолютной и относительной погрешностей от результата измерений для прибора с преобладающими мультипликативными погрешностями Задание 3 Цифровым амперметром класса точности 0,25/0,1 со шкалой (0...5) А измерены значения температуры 0; 0,5; 1,0; 1,5; 2,0; 3,0; 4,0; 5,0 А. Рассчитать зависимости абсолютной и относительной основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков. Для записи результатов формируем таблицу 3.3, в столбцы которой будем записывать измеренные значения I, абсолютные ΔI и относительные δI погрешности. Таблица 3.3 – Результаты расчёта значений погрешностей
В первый столбец записываем заданные в условии задачи измеренные значения температуры 0; 0,5; 1,0; 1,5; 2,0; 3,0; 4,0; 5,0 А. Класс точности термометра задан в виде двух чисел, разделённых косой чертой. Следовательно, относительная погрешность, выраженная в процентах, во всех точках шкалы должна удовлетворять следующему соотношению
В данном случае а = 0,25; b = 0,1; Ik= 5 А, причём параметры этой формулы а и b определяются мультипликативной и аддитивной составляющими суммарной погрешности соответственно. Таким образом, получаем
При решении рассмотрим худший случай
что соответствует Примем во внимание опыт решения задачи 1, из которого видно, что результаты вычисления, выполненные для положительных и отрицательных значений погрешностей, численно совпадают друг с другом и отличаются только знаками «+» или «−». Поэтому дальнейшие вычисления будем производить только для положительных значений относительной погрешности
но при этом будем помнить, что все значения второго и третьего столбцов таблицы 3.3 могут принимать и отрицательные значения. Рассчитаем значения относительной погрешности. При I = 0 А получаем
При I = 10 А получаем
При I = 20 А получаем
При I = 40 А получаем
При I = 50 А получаем
При I = 60 А получаем
При I = 80 А получаем
При I = 100 А получаем
Полученные значения относительной погрешности заносим в третий столбец таблицы 3.3. Рассчитаем значения абсолютной погрешности. Из формулы При I=0 А получаем Искомое значение ΔIможно определить следующим образом. Так как класс точности прибора задан в виде двух чисел, то у данного прибора аддитивные и мультипликативные погрешности соизмеримы. При I = 0 А мультипликативная составляющая погрешность равна нулю, значит, общая погрешность в этой точке обусловлена только аддитивной составляющей. Аддитивную составляющую представляет второе из чисел, задающих класс точности, т.е. в данном случае число b = 0,1. Это означает, что аддитивная погрешность составляет 0,1 % от верхнего предела измерений прибора, т.е. от I К = 5 А. Таким образом, при I = 0 имеем
При I = 0,5 А получаем При I = 1 А получаем При I = 1,5 А получаем При I = 2 А получаем При I = 3 А получаем При I = 4 А получаем При I = 5 А получаем Полученные таким образом значения абсолютной погрешности заносим во второй столбец таблицы 3.3. По данным таблицы 3.3, учитывая, что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной ΔI и относительной δI погрешностей от результата измерений I (рисунок 3.3).
Рисунок 3.3 – Графики зависимостей абсолютной и относительной погрешностей от результата измерений для прибора с соизмеримыми аддитивными и мультипликативными погрешностями
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

 .
. ,654.
,654. ,
,
 ,
, Оцениваем дисперсию искомого результата
Оцениваем дисперсию искомого результата
 Находим эффективное число степеней свободы выборок двух аргументов Х1 и Х2
Находим эффективное число степеней свободы выборок двух аргументов Х1 и Х2 искомого результата:
искомого результата: .
.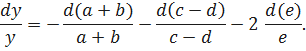
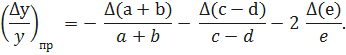
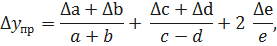
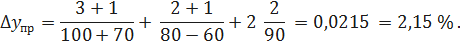
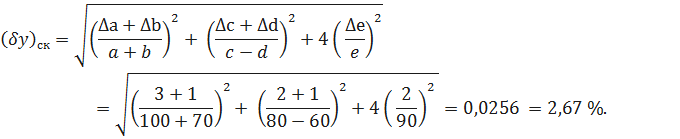
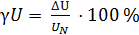 выражаем абсолютную погрешность
выражаем абсолютную погрешность 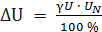 . За нормирующее значение UN принимаем размах шкалы, так как шкала
. За нормирующее значение UN принимаем размах шкалы, так как шкала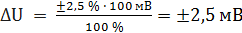 во всех точках шкалы прибора. Заносим данное значение во второй столбец таблицы.
во всех точках шкалы прибора. Заносим данное значение во второй столбец таблицы.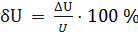 .
.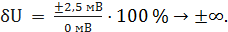
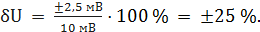
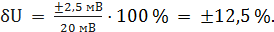
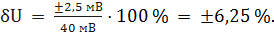
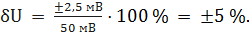
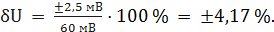
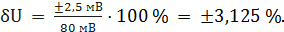
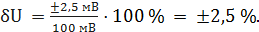
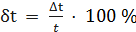 выражаем абсолютную погрешность:
выражаем абсолютную погрешность: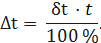
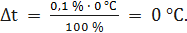


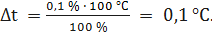
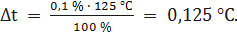
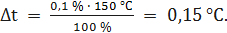
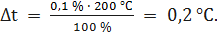
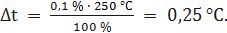

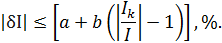

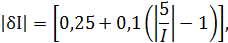
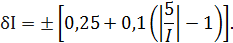
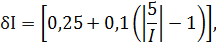
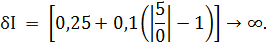

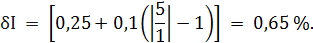
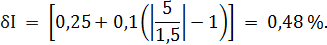
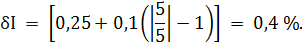
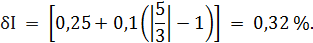
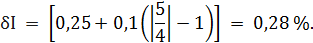
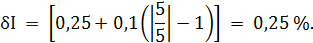
 выражаем абсолютную погрешность:
выражаем абсолютную погрешность: 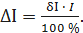
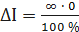 - неопределённость.
- неопределённость.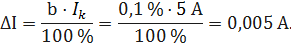
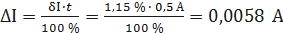 .
.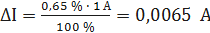 .
.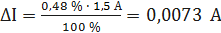 .
.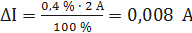 .
.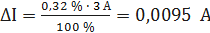 .
.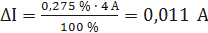 .
.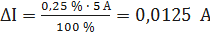 .
.



