
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямые однократные измеренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прямые многократные измерения в большей мере относятся к лабораторным измерениям. Для производственных процессов более характерны однократные измерения. Однократные измерения являются самыми массовыми и проводятся, если: при измерении происходит разрушение объекта измерения, отсутствует возможность повторных измерений, имеет место экономическая целесообразность. Последовательность действий при выполнении этих измерений следующая. 1. Анализ априорной информации. Эти измерения возможны лишь при определенных условиях: - объем априорной информации об объекте измерений такой, что модель объекта и определение измеряемой величины не вызывают сомнений; - изучен метод измерения, его погрешности либо заранее устранены, либо оценены; - СИ исправны, а их метрологические характеристики соответствуют установленным нормам. Итогом анализа условий должна стать уверенность в том, что точности однократного измерения достаточно для выполнения поставленной задачи. 2. За результат прямого однократного измерения принимается полученная величина (значение отсчета). 3. Внесение в отсчет поправки q. 4. Определение максимально возможного отклонения результата измерения от истинного значения измеряемой величины. Составляющими погрешности прямых однократных измерений являются: - погрешности СИ, рассчитываемые по их метрологическим характеристикам; - погрешность используемого метода измерений, определяемая на основе анализа в каждом конкретном случае; - личная погрешность, вносимая оператором. Если последние две составляющие не превышают 15% погрешности СИ, то за погрешность результата однократного измерения принимают погрешность используемого СИ Перечисленные составляющие могут состоять из неисключенных систематических (после введения поправки) и случайных погрешностей. Распределение случайных погрешностей обычно принимают по нормальному закону, а неисключенных систематических по равномерному. Они могут быть представлены своими границами ±Qi, либо доверительными границами ±Qi (Р). Если неисключенные систематические погрешности есть только у одной из составляющих, то она и определяет границы этой погрешности ±Qi. При наличии нескольких неисключенных систематических погрешностей доверительную границу вычисляют по формуле
где
При Параметр l = Случайные составляющие погрешности результата измерений выражаются либо своими СКО Таблица 3.6
Значения коэффициента k в зависимости от m и l при Р = 0,99
В первом случае доверительная граница случайной составляющей погрешности результата прямого однократного измерения определяется через его СКО
где
В случае, когда случайные погрешности представлены доверительными границами
Если случайные погрешности представлены доверительными границами
Найденные значения
1. Если 2. Если 3. Если
где k – коэффициент, принимаемый по табл.3.7. в зависимости от вероятности Р. Таблица 3.7
Значения коэффициента k в зависимости от соотношения Q/Sx
Кроме изложенного метода, суммирование случайных и систематических составляющих может производиться и другими методами. Результат прямых однократных измерений при симметричном распределении погрешностей должен записываться в соответствии с рекомендациями МИ 1317-86 в виде Пример 3.3. При измерении внутреннего диаметра втулки Æ10мм проводилась настройка измерительного прибора на нулевую отметку по концевой мере 10 мм. Размер концевой меры по аттестату равен 10,001мм. Абсолютная погрешность настройки равна 3,5мкм. Отсчет подчиняется равномерному закону распределения вероятностей с предельными отклонениями D = ±0,8 мкм. Показание прибора равно – 3 мкм. Определить и записать результат измерений. Решение. 1. Значение отсчета и показания равны х = - 0,003мм. 2. Определяются значения составляющих систематических погрешностей. Они складываются из погрешности концевой меры и погрешности настройки измерительного прибора. Погрешность концевой меры, которую мы можем исключить путем введения поправки,определяется разностью номинального размера и размера по аттестату Dм = 10,000-10,001 = - 0,001 мм. Отсюда значение поправки q = - Dм = 0,001 мм. Погрешность настройки измерительного прибора остается неисключенной: 3. Определяется случайная погрешность. Эта погрешность для равномерного закона распределения погрешности отсчета равна предельному отклонению e = D = ± 0,0008 мм. 4. С целью выбора способа суммирования неисключенной систематической и случайной погрешности определяется их соотношение 5. Рассчитывается погрешность измерения. В соответствии с полученным соотношением Задаемся доверительной вероятностью Р = 0,95, тогда по табл.3.7 получим коэффициент k = 0,72. В соответствии с уравнением (3.14) погрешность измерения равна D = 0,72 (3,5 + 0,8) = 3,096мкм» 0,003мм.
5. Рассчитывается и записывается в соответствии с п.3.1 результат измерения. Исправленный результат измерения Х = хном + х +q = 10,000 + (-0,003) + 0,001 = 9,998 мм. Доверительные границы истинного размера диаметра 9,995мм £ D £ 10,001мм, а при симметричном распределении погрешностей можно записать D = (9,998±0,003) мм, Р = 0,95.
Косвенные измерения При косвенных измерениях погрешность результата зависит от погрешности каждого из прямых измерений. Результат
Так как каждое Например, пусть При функции Так как возможные функции
Разложим эту функцию в ряд Тейлора
Полагая, что погрешности второго порядка пренебрежимо малы, можем записать
Отсюда, так как
Полученные таким путем значения Аналогично этому, если известны среднеквадратичные отклонения (СКО) случайной абсолютной погрешности
Для коррелированных составляющих
Особенностью метода частных производных для расчета результирующей погрешности результата Для простейших функций Так, для функции вида
то есть абсолютная погрешность суммы просто равна сумме абсолютных погрешностей слагаемых. Однако, относительная погрешность суммы равна
то есть является сложной функцией, зависящей не только от погрешностей слагаемых, но и от сочетания значений самих измеренных слагаемых. Для функции вида
и после дифференцирования
Заменяя дифференциалы малыми конечными приращениями (чем погрешность по существу и является), получим
или то есть относительная погрешность произведения просто равна сумме относительных погрешностей сомножителей. Зато абсолютная погрешность в этом случае равна
то есть зависит не только от значений Сформулированные простейшие правила определения погрешности результата Но если при этом погрешности Так, например, для функции вида
Отсюда
но для некоррелированных погрешностей
Таким образом, дисперсия разности двух СВ равна не разности, а сумме их дисперсий. Поэтому, несмотря на отрицательные знаки частных производных, погрешности составляющих должны не вычитаться, а складываться. То же самое должно производится при расчете относительной погрешности не произведения, а частного. Хотя, например, для функции вида Использованный выше прием логарифмирования и последующего дифференцирования функции Например, для ранее приведенной функции Если
Итогом проведенного рассмотрения является то, что расчет погрешности результатов косвенных измерений складывается из двух этапов. 1-й этап – вывод формулы для абсолютной или относительной погрешности результата косвенного измерения, исходя из вида функции 2-й этап – расчет погрешности Z в соответствии с полученной формулой путем суммирования ее составляющих по правилам суммирования случайных погрешностей с учетом корреляционных связей и их законов распределения.
Пример 3.4. Известно, что коэффициент деления входного измерительного делителя напряжения равен
Решение. Погрешность коэффициента деления определяем методом частных производных по выражению
Поскольку величины сопротивлений не коррелированы между собой, то получаемые выражения для погрешностей надо суммировать, то есть брать по модулю. По условию задачи даны относительные погрешности сопротивлений, В полученном выражении каждое слагаемое умножим и разделим на сопротивление, соответствующее погрешности DRi, получим
ЗАДАНИЯ ПО РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЕ
1. Толщиномером, имеющим класс точности 1,5, получены результаты измерений толщины лакового покрытия в мкм: 470, 550, 354, 402, 434, 387, 415, 465, 447, 547, 394, 425, 459, 442, 413, 415, 488, 481, 477, 380. Измерения выполнялись при температуре 30 оС. Коэффициент линейного расширения лака имеет равномерный закон распределения и, по справочным данным, находится в пределах: a = (35 ¸ 64)×10-6. Определить и записать результат измерений. 2.Прибором для измерений толщины покрытий, использующим метод неразрушающего контроля и имеющим класс точности 0,5, получены результаты измерений толщины золотого покрытия корпусов интегральных схем в мкм: 4,15; 5,88; 5,77; 4,77; 4,85; 5,81; 5,11; 5,49; 5,48; 5,56; 4,23; 5,21; 5,99; 5,55; 5,90; 5,43; 4,48; 6,12; 4,99; 5,25; 6,62; 7,95; 6,31; 6,91; 5,88; 5,75; 5,33; 5,94; 6,23; 6,66. Измерения выполнялись при температуре 28оС. Коэффициент линейного расширения золота имеет нормальный закон распределения и, по справочным данным, находится в пределах: a = (3 ¸ 6)×10-5. Определить и записать результат измерений. 3. Косвенным методом измеряют выходное напряжение инвертирующего операционного усилителя (масштабирующего измерительного преобразователя) по результатам прямого измерения омметром классом точности III входного сопротивления R1 номиналом 20 кОм и сопротивления обратной связи R2 номиналом 10 кОм. Были соответственно получены следующие результаты измерений: R1 – 13,74; 19,47; 19,10; 15,79; 16,06; 19,24; 16,92; 14,87; 18,14; 18,41; 14,00; 17,25; 19,83; 18,37; 19,53; 17,98; 14,83; 20,26; 16,52; 17,38; 21,92; 26,32; 20,89; 22,88; 19,47; 19,04; 17,65; 19,67; 22,05; 20,63, а R2 - 7,10; 10,06; 9,87; 8,16; 8,30; 9,94; 8,74; 7,68; 9,37; 9,51; 7,24; 8,91; 10,25; 9,49; 10,09; 9,29; 7,66; 10,47; 8,54; 8,98; 11,32; 13,60; 10,79; 11,82; 10,06; 9,84; 9,12; 10,16. Входное напряжение 1В было измерено с относительной погрешностью 0,2%. Выходное напряжение связано с входным соотношением записать результат измерений. 4. Мощность, поглощаемую в сопротивлении R, определяют путем измерения приложенного напряжения с последующим вычислением по формуле
точности 1%. Многократные измерения напряжения 100 В показали следующий результат: 75,58; 107,09; 105,09; 86,87; 88,33; 105,81; 93,07; 81,77; 99,80; 101,26; 77,04; 94,89; 109,09; 101,08; 107,45; 98,89; 81,59; 111,46; 90,88; 65,61. Сопротивление R номиналом 1 кОм имеет отклонение от номинала равное ± 5%. Измерения проводились при температуре 30оС. Температурный коэффициент сопротивления равен: a = (3,5 ¸ 5,1)×10-4. Результат измерений сопротивления: 0,78; 1,11; 1,08; 0,90; 0,91; 1,09; 0,96;0,84; 1,03; 1,04; 1,11; 1,02; 0,84; 1,15; 0,94; 0,99; 1,24; 1,49; 1,19; 1,30. Распределение нормальное. Определить и записать результат измерений. 5. См. задание 4 с изменениями. Вольтметр класса точности 0,02/0,01; результаты измерения напряжения распределены по нормальному закону; результаты измерения сопротивления распределены по закону Симпсона. Определить и записать результат измерений 6. См. задание 4 с изменениями. Вольтметр класса точности С. результаты измерения напряжения и сопротивления распределены по нормальному закону. Определить и записать результат измерений. 7. Коэффициент деления входного измерительного делителя напряжения равен Кдел = R3/(R1+ R2 - R3), где номинальные значения R1 = 5 кОм, R2 = 2 кОм, R3 = 3 кОм. Измерения проводились при температуре 30оС, омметр имеет класс точности 2,5%, температурный коэффициент сопротивлений равен: a = (3,5 ¸ 5,1)×10-4. Значения сопротивлений распределены по нормальному закону. Результаты измерений: R1 - 5,35; 4,63; 6,63; 5,51; 4,25; 4,99; 6,22; 6,15; 4,87; 5,81; 5,62; 5,73; 7,71; 5,89; 5,48; 5,75; 5,31. R2 – 2,02; 1,74; 2,50; 2,07; 1,60; 1,88; 2,34; 2,32; 1,83; 2,19; 2,12; 2,16; 2,91; 2,22; 2,06; 2,17; 2,00. R3 - 2,91; 2,52; 3,61; 2,99; 2,31; 2,71; 3,38; 3,34; 2,65; 3,16; 3,06; 3,12; 4,19; 3,20; 2,98; 3,13; 2,89. Определить погрешность коэффициента деления. 8. См. задание 7 с изменениями. Омметр имеет аддитивную относительную погрешность dа = 0,1%, мультипликативную относительную погрешность dм = 0,2% и номинальный коэффициент преобразования равный 1. 9. Оценить погрешность результата однократного измерения напряжения U = 1,5В на входном сопротивлении R = 6 Ом, выполненного вольтметром класса точности 0,5 с верхним пределом
диапазона измерений U = 10 В и имеющим внутреннее сопротивление Rv = 1300 Ом. Дополнительные погрешности показаний СИ из-за влияния магнитного поля и температуры не превышают соответственно dмп = ± 0,65% и dт = ± 0,25% допускаемой предельной погрешности. 10. Для измерения длины использовалась линейка из тугоплавкого сплава при температуре выше нормальной на 950 К. Получено значение показания равное 0,9 м. Известно, что отсчет подчиняется нормальному распределению вероятностей с s = 0,003 м. Коэффициент линейного расширения сплава может быть в пределах a = (10-6…10-5) К-1. Определить температурную поправку и доверительные границы значения измеряемой величины. Записать результат измерения. 11. Измерение диаметра металлического вала Æ35 мм при температуре 100 оС производилось индикаторным измерителем с настройкой на нулевую отметку по концевой мере. Действительный размер концевой меры по аттестату 34,998 мм при температуре 20 оС. Температурный коэффициент сплава, из которого изготавливается вал, равен a = (35 … 250) 10-6 К-1. Погрешность настройки равна 1, 5 мкм. Отсчет подчиняется равномерному закону распределения с предельным отклонениями D = ± 3 мкм. Показания индикатора равно ± 7 мкм. Определить и записать доверительные границы размера. 12. Найти погрешность волнового сопротивления линии r, которое связано с индуктивностью и емкостью линии соотношением 13. Цифровым измерителем иммитанса Е7 – 14 проводились прямые многократные измерения сопротивления магазина сопротивлений, номинальное значение которого равно 0,1 Ом. Получены следующие результаты измерения R: 168,61; 168,55; 168,61; 168,55; 168,61; 168,59; 168,57; 168,56; 168,57; 168,58; 170,73; 168,62; 168,60; 168,63; 168,54; 168,59 мОм. Проведенные измерения характеризуются неисключенной систематической погрешностью, задаваемой пределом допускаемого значения: - основной погрешности измерения измерителя. Формула для расчета ее значения имеет следующий вид: 10-3·(1+Q)·R + 3·10-4 Rк, где Rк = 1 Ом, добротность Q = 0; - дополнительной погрешности измерения, равной удвоенному допускаемому значению основной погрешности. Для устранения влияния соединительных проводов и переходных сопротивлений контактов был проведен ряд измерений при нулевом значении магазина сопротивлений. Получены следующие результаты измерений Rо : 53,69; 53,68; 53,67; 53,68; 53,67; 53,68; 54,87; 53,67; 53,69; 53,54; 53,69; 53,69; 53,70; 53,74; 53,69. Найти суммарную погрешность измерения сопротивлений. 14. См. задание 13 с изменениями. Результаты измерения R: 154,40; 154,33; 154,41; 154,37; 154,38; 154,38; 154,37; 154,36; 156,22; 154,41; 154,39; 154,42; 154,35; 154,44. Результаты измерения Rо: 55,43; 55,42; 55,41; 55,43; 55,41; 55,42; 55,44; 55,41; 55,43; 56,99; 55,43; 55,43; 55,44; 55,45; 55,43. Найти суммарную погрешность измерения сопротивлений. 15. См. задание 13 с изменениями.. Результаты измерения R: 157,40; 157,32; 157,40; 157,37; 157,38; 157,35; 157,37; 157,36; 155,22; 157,41; 157,39; 157,42; 157,35; 156,44. Результаты измерения Rо: 58,41; 58,42; 58,41; 58,43; 58,41; 58,42; 58,44; 58,41; 58,43; 55,99; 58,43; 58,43; 58,44; 58,45; 58,43. Найти суммарную погрешность измерения сопротивлений. 16. Определить и записать расчетную формулу погрешности канала измерения мощности, представленного на рис. 4.1. На рис. 4.1 ТТ и ТН – соответственно трансформаторы тока и напряжения; ПРР и ПРI – преобразователи соответственно мощности и тока; К – коммутатор; АЦП – аналого - цифровой преобразователь. Исходные данные: относительная погрешность ТТ, приведенная к началу диапазона измерения, составляет
тых ключом каналов (0,13) и от пульсации несущей частоты (0,06%);
17. См. задание 16 с изменениями. Закон распределения результирующей погрешности – нормальный. 18. См. задание 16 с изменениями. Закон распределения погрешности АЦП – нормальный. 19. Сопротивление R определяют по закону Ома путем измерения приложенного напряжения и протекающего тока. Вольтметр имеет класс точности 1,5%. Амперметр имеет класс точности 0,5%. Многократные измерения напряжения и тока показали соответственно следующий результат: U, В - 237,8; 242,2; 233,4; 238,8; 240,0; 239,2; 235,5; 234,6; 236,7; 242,5; 241,17; 235,18; 239,11; I, А – 1,05; 1,09; 1,06; 1,07; 1,08; 1,09; 1,08; 1,05; 0,99;1,04; 1,05;а 1,06. Измерения проводились при температуре 30оС. Температурный коэффициент сопротивления равен: a = (3,5 ¸ 5,1)×10-4. Распределение нормальное. Определить и записать результат измерений. 20. Рассчитать результирующую погрешность измерительного канала, состоящего из трех узлов: датчика Д, усилителя У и регистратора Р. Датчик имеет внутреннее сопротивление 150 Ом и погрешность g = 0,15%, питается напряжением 200 мВ через стабилизатор с коэффициентом стабилизации К = 30 от общего с усилителем блока питания. Коэффициент влияния колебаний напряжения питания U равен yUУ = +0,3% / (10% DU/U), а влияние температуры приводит к смещению его нуля на y0У = + 0,2%/10К. В
качестве регистратора используется компьютер, имеющий погрешность, соответствующую классу точности 0,2/0,1.Установка питается от сети 220 В, 50 Гц с нестабильностью напряжения ± 15%. На датчик в цеху воздействует температура в пределах (20± 15) оС, а на усилитель и регистратор, установленные в лаборатории, в пределах от 19 до 26 оС. Датчик связан с приборами кабелем, сопротивление каждой из двух жил которого равно 2 Ом. Напряжение наводки частотой 50 Гц измерено цифровым электронным вольтметром с входным сопротивлением 1 Мом, составляет 1,6 В. 21. См. задание 20 с изменениями. Погрешность датчика g = 0,35%. Коэффициент влияния колебаний напряжения питания U равен yUУ = +0,5% / (10% DU/U), а влияние температуры приводит к смещению его нуля на y0У = + 0,4%/10К. Установка питается от сети 220 В, 50 Гц с нестабильностью напряжения ± 20%. Датчик связан с приборами кабелем, сопротивление каждой из двух жил которого равно 3,5 Ом. Напряжение наводки частотой 50 Гц измерено электронным вольтметром с входным сопротивлением 1,5 Мом, составляет 0,6 В. 22. См. задание 20 с изменениями. Погрешность датчика g = 0,25%. Коэффициент влияния колебаний напряжения питания U равен yUУ = +0,4% / (10% DU/U), а влияние температуры приводит к смещению его нуля на y0У = + 0,35%/10К. Установка питается от сети 220 В, 50 Гц с нестабильностью напряжения ± 10%.Датчик связан с приборами кабелем, сопротивление каждой из двух жил которого равно 4,5 Ом. Напряжение наводки частотой 50 Гц измерено электронным вольтметром с входным сопротивлением 2,5 Мом, составляет 0,8 В. 23. См. задание 20 с изменениями. Погрешность датчика g = 0,3%. Коэффициент влияния колебаний напряжения питания U равен yUУ = +0,45% / (10% DU/U), а влияние температуры приводит к смещению его нуля на y0У = + 0,45%/10К. Установка питается от сети 220 В, 50 Гц с нестабильностью напряжения ± 7%.Датчик связан с приборами кабелем, сопротивление каждой из двух жил которого равно 1,5 Ом. Напряжение наводки частотой 50 Гц измерено электронным вольтметром с входным сопротивлением 0,5 Мом, составляет 2,2 В.
24. Напряжение источника ЭДС Ux с внутренним сопротивлением Ri = 45±7 Ом измерено вольтметром класса точности 1,5. Сопротивление вольтметра Rv = 6 кОм и известно с погрешностью ±0,9%. Показание вольтметра Uv = 12,35 В. Найти поправку, которую нужно внести в показание прибора для определения действительного значения напряжения источника ЭДС. 25. Найти волновое сопротивление при температуре 20 оС линии 26. Определить границы доверительного интервала при измерении давления p = F/S с вероятностью Р = 0,9, если при многократных измерениях получены следующие результаты: для F, Н – 260; 261; 262; 272; 263; 265; 280; 267; 268; 263; 266; 266; 265; 270; 271, а для площади S, 10-6м2 – 1,366; 1,377; 1,362; 1,365; 1,369; 1,368; 1,369; 1,365; 1,367; 1,372; 1,368; 1,366; 1,368; 1,369; 1,366. Измерительные приборы для измерения имели класс точности 2,5. 27. При определении сопротивления были получены следующие измерения напряжения и силы тока: U, В – 115,12; 115,32; 115,25; 115,28; 115,31; 115,43; 115,30; 115,18; 115,20; 115,19; 115,22; 115,29; 115,27; 115,26; 115,13; I, А – 2,38; 2,39; 2,52; 2,44; 2,45; 2,39; 2,66; 2,48; 2,43; 2,49; 2,50; 2,48; 2,40; 2,41; 2,49. Измерительные приборы имели класс точности 1,5. Определить границы доверительного интервала для измеренного значения сопротивления. 28. При многократных измерениях g - излучения дозиметр, имеющий класс точности 2, показал следующие результаты: 37,30; 37,29; 37,28; 37,29; 37,28; 37,26; 37,27; 37,38; 37,31; 37,32; 37,30; 37,30; 37,29; 37,30, 37,29. Измерения проводились при температуре 35 о |

 , (3.10)
, (3.10)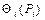 – доверительная граница
– доверительная граница 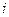 – й неисключенной систематической погрешности, соответствующей доверительной вероятности
– й неисключенной систематической погрешности, соответствующей доверительной вероятности 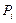 ;
;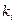 – коэффициент, зависящий от доверительной вероятности, с которой определены границы
– коэффициент, зависящий от доверительной вероятности, с которой определены границы  – коэффициент, определяемый принятой доверительной вероятностью
– коэффициент, определяемый принятой доверительной вероятностью 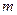 и их соотношением. При
и их соотношением. При  он мало зависит от числа слагаемых и может быть представлен усредненными значениями: при Р = 0,90 коэффициент k = 0,95; Р = 0,95 k = 1,1; Р = 0,99 k = 1,4.
он мало зависит от числа слагаемых и может быть представлен усредненными значениями: при Р = 0,90 коэффициент k = 0,95; Р = 0,95 k = 1,1; Р = 0,99 k = 1,4. коэффициент k значительно зависит от числа слагаемых и соотношения между ними. Если
коэффициент k значительно зависит от числа слагаемых и соотношения между ними. Если  , то рекомендуется принимать среднее значение k = 1,4, при
, то рекомендуется принимать среднее значение k = 1,4, при 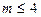 значение k необходимо определять по графику ГОСТ 8.207 – 76 или табл.3.6.
значение k необходимо определять по графику ГОСТ 8.207 – 76 или табл.3.6.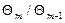 принимается равным наименьшему значению этого отношения при условии, что
принимается равным наименьшему значению этого отношения при условии, что 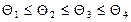 .
. , либо доверительными границами
, либо доверительными границами 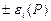 .
.
 (3.11)
(3.11) (или
(или 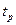 ) – точка нормированной функции Лапласа, соответствующая вероятности Р и определяемая по табл.П.1;
) – точка нормированной функции Лапласа, соответствующая вероятности Р и определяемая по табл.П.1; (3.12)
(3.12)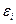 с разными доверительными вероятностями
с разными доверительными вероятностями  , то
, то (3.13)
(3.13) и
и  используются для оценки погрешности результата прямых однократных измерений. В зависимости от их соотношения могут быть различные варианты.
используются для оценки погрешности результата прямых однократных измерений. В зависимости от их соотношения могут быть различные варианты. , то пренебрегают неисключенными систематическими погрешностями и граница результата измерения равна
, то пренебрегают неисключенными систематическими погрешностями и граница результата измерения равна  .
. , то пренебрегают случайными погрешностями и за границу результата измерения принимают границы неисключенных систематических погрешностей
, то пренебрегают случайными погрешностями и за границу результата измерения принимают границы неисключенных систематических погрешностей  .
. , то доверительные границы
, то доверительные границы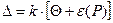 (3.14)
(3.14)
 при доверительной вероятности Р = Рд.
при доверительной вероятности Р = Рд. , где
, где 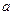 – параметр равномерного закона распределения равный предельному отклонению ± 0,8 мкм. Следовательно, Sx = 0,8× 3 = 1,386мкм. Соотношение
– параметр равномерного закона распределения равный предельному отклонению ± 0,8 мкм. Следовательно, Sx = 0,8× 3 = 1,386мкм. Соотношение  косвенного измерения определяется расчетом по измеренным значениям
косвенного измерения определяется расчетом по измеренным значениям 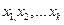 и заранее известной функции
и заранее известной функции (3.15)
(3.15)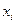 , где
, где 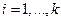 измерено с соответствующей погрешностью
измерено с соответствующей погрешностью  , то задача расчета погрешности
, то задача расчета погрешности  результата
результата  , но
, но 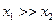 и
и  . В этом случае погрешность в 1%, допущенная при измерении
. В этом случае погрешность в 1%, допущенная при измерении  внесет в результат Z относительную погрешность всего в 0,01%, но такая же погрешность в 1%, допущенная при измерении
внесет в результат Z относительную погрешность всего в 0,01%, но такая же погрешность в 1%, допущенная при измерении  , практически полностью войдет в погрешность результата Z.
, практически полностью войдет в погрешность результата Z.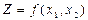 вида
вида  независимо от соотношения между собой
независимо от соотношения между собой  и
и  , погрешность измерения
, погрешность измерения  , а погрешность измерения
, а погрешность измерения 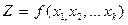 и соотношения
и соотношения  (3.16)
(3.16)
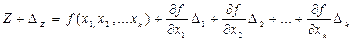
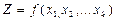 , то
, то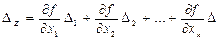
 при данном сочетании
при данном сочетании  можно рассматривать как веса, с которыми в суммарную абсолютную погрешность
можно рассматривать как веса, с которыми в суммарную абсолютную погрешность  входят составляющие в виде абсолютных погрешностей измерения каждого из
входят составляющие в виде абсолютных погрешностей измерения каждого из  , возникающая от абсолютной погрешности
, возникающая от абсолютной погрешности  будет равна
будет равна  .
. отдельных
отдельных  . Суммарная погрешность
. Суммарная погрешность  (3.17)
(3.17) и
и 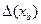 результирующая погрешность определяется как их алгебраическая сумма, но с учетом весов
результирующая погрешность определяется как их алгебраическая сумма, но с учетом весов 
 (3.18)
(3.18) косвенных измерений является то, что он правомерен только для абсолютных погрешностей. Относительные их значения должны находится соответствующим пересчетом.
косвенных измерений является то, что он правомерен только для абсолютных погрешностей. Относительные их значения должны находится соответствующим пересчетом.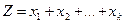 все частные производные
все частные производные  равны единице и поэтому
равны единице и поэтому и
и  (3.19)
(3.19) , (3.20)
, (3.20) наоборот, относительная погрешность
наоборот, относительная погрешность 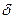 очень просто выражается через относительные погрешности аргументов
очень просто выражается через относительные погрешности аргументов  . Действительно, если уравнение этой функции прологарифмировать, то получим
. Действительно, если уравнение этой функции прологарифмировать, то получим
 .
. , (3.21)
, (3.21)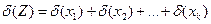 . (3.22)
. (3.22) ,
, .
.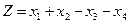 частные производные равны соответственно
частные производные равны соответственно ,
,  ,
,  ,
, 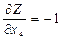 .
. ,
, .
. после логарифмирования
после логарифмирования  относительные погрешности должны всегда складываться, если только они жестко не коррелированы.
относительные погрешности должны всегда складываться, если только они жестко не коррелированы. удобно использовать во всех случаях, когда это оказывается возможным.
удобно использовать во всех случаях, когда это оказывается возможным. и
и 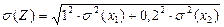 , где
, где  и
и  – относительные значения СКО погрешностей
– относительные значения СКО погрешностей  .
. , то
, то 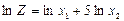 и СКО относительной погрешности будет
и СКО относительной погрешности будет 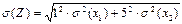 и так далее.
и так далее. .
. , где номинальные значения
, где номинальные значения  ,
,  ,
, 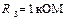 . В результате прямых измерений сопротивлений, которые выпускаются с относительной погрешностью 5%, измерить (найти) косвенным методом погрешность коэффициента деления.
. В результате прямых измерений сопротивлений, которые выпускаются с относительной погрешностью 5%, измерить (найти) косвенным методом погрешность коэффициента деления.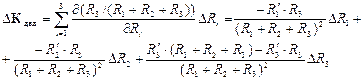 .
. , поэтому надо абсолютные погрешности
, поэтому надо абсолютные погрешности  привести к относительным
привести к относительным  .
. .
. . С какой погрешностью было выполнено косвенное измерение выходного напряжения? Определить и
. С какой погрешностью было выполнено косвенное измерение выходного напряжения? Определить и . Вольтметр имеет класс
. Вольтметр имеет класс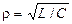 Прямые измерения проводились мостовым измерителем L, C, R класса точности 0,02/0,01. Получены следующие результаты измерений: L,мкГн - 5,38; 4,64; 6,73; 5,61; 4,27; 4,99; 6,26; 6,18; 4,77; 5,83; 5,62; 5,73; 7,71; 5,89; 5,48; 5,77; 5,31. С, пкФ – 2,12; 1,76; 2,55; 2,07; 1,60; 1,88; 2,34; 2,32; 1,83; 2,19; 2,12; 2,16; 2,91; 2,22.
Прямые измерения проводились мостовым измерителем L, C, R класса точности 0,02/0,01. Получены следующие результаты измерений: L,мкГн - 5,38; 4,64; 6,73; 5,61; 4,27; 4,99; 6,26; 6,18; 4,77; 5,83; 5,62; 5,73; 7,71; 5,89; 5,48; 5,77; 5,31. С, пкФ – 2,12; 1,76; 2,55; 2,07; 1,60; 1,88; 2,34; 2,32; 1,83; 2,19; 2,12; 2,16; 2,91; 2,22. а к концу -
а к концу -  ; относительная погрешность ТН dТН = 0,5%; СКО погрешности преобразования мощности состоит из пяти составляющих: основной погрешности (1%); погрешности от пульсации (0,2%); дополнительной погрешности от изменения
; относительная погрешность ТН dТН = 0,5%; СКО погрешности преобразования мощности состоит из пяти составляющих: основной погрешности (1%); погрешности от пульсации (0,2%); дополнительной погрешности от изменения  (0,15%); погрешности от колебания напряжения питания (0,1%) и от колебаний температуры окружающей среды (0,6%);
(0,15%); погрешности от колебания напряжения питания (0,1%) и от колебаний температуры окружающей среды (0,6%);  ,
,  . Закон распределения результирующей погрешности и погрешности АЦП – равномерный.
. Закон распределения результирующей погрешности и погрешности АЦП – равномерный.

 , если прямыми измерениями при температуре 30 оС получены следующие значения индуктивности и емкости: L, мГн – 37,30; 37,29; 37,28; 37,29; 37,28; 37,40; 37,29; 37,26; 37,30; 37,31; 37,27; 37,28; 37,32; 37,31; 37,27; С, пкФ – 156,52; 156,44; 156,51; 156,46; 156,52; 156,50; 156,49; 156,47; 156,48; 156,49; 156,75; 156,55; 156,51; 156,53; 156,48. Измеритель L, C имеет класс точности 1,5%. Температурные коэффициенты соответственно равны aL = (0,5¸1) мГн/К; aC = (1¸ 2,5) пкФ/К.
, если прямыми измерениями при температуре 30 оС получены следующие значения индуктивности и емкости: L, мГн – 37,30; 37,29; 37,28; 37,29; 37,28; 37,40; 37,29; 37,26; 37,30; 37,31; 37,27; 37,28; 37,32; 37,31; 37,27; С, пкФ – 156,52; 156,44; 156,51; 156,46; 156,52; 156,50; 156,49; 156,47; 156,48; 156,49; 156,75; 156,55; 156,51; 156,53; 156,48. Измеритель L, C имеет класс точности 1,5%. Температурные коэффициенты соответственно равны aL = (0,5¸1) мГн/К; aC = (1¸ 2,5) пкФ/К.


