
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы нормирования погрешности. КлассСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ Методические указания к выполнению расчетно-графических работ
Йошкар-Ола МАРИЙСКИЙ ГОСУДАРСТВЕНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ УДК 389 (076) ББК 30.10 М 54
Рецензент: канд.техн.наук, доцент МарГТУ В.В.Кошкин. Печатается по решению редакционно-издательского совета МарГТУ.
М 54 Метрология, стандартизация и сертификация: методические указания к выполнению расчетно-графических работ. / Сост. Н.Г. Моисеев. – Йошкар-Ола: Марийский государственный технический университет, 2007. – 78 с.
Представлены классификация и описание погрешностей результатов и средств измерений, расчет погрешностей результатов прямых, однократных, многократных, косвенных измерений. Даны задания для выполнения расчетно-графических работ. Для студентов специальностей 230100.62, 230101, 230105 направления «Информатика и вычислительная техника»
УДК 389(076) ББК 30.10 © Марийский государственный технический университет, 2007 ВВЕДЕНИЕ
Измерения с целью определения значений физических величин (массы, длины, скорости и др.) являются главным источником информации во всех сферах деятельности человека. Но из-за несовершенства методов и средств измерений, влияния внешних воздействующих факторов (температуры окружающей среды, ее давления и влажности, вибрации, ускорения, излучений и др.), человеческого фактора истинные значения этих величин получить нельзя. Значения физических величин, полученные измерением, лишь в большей или меньшей степени приближаются к ним. Отклонение результата измерения от истинного значения измеряемой величины называется погрешностью измерения. Так как истинные значения величины установить нельзя, то нужно хотя бы определить границы, в пределах которых оно может находиться с заранее заданной вероятностью. Освоение теоретических положений и решение заданий, представленных в данном методическом пособии, позволит приобрести навыки по определению доверительных или предельных границ истинного значения измеряемой величины – погрешности измерения. Способы определения погрешностей при различных видах измерения будут разными. В свою очередь, погрешности средств измерений в нормативно-технической документации могут быть представлены по-разному: метрологическими характеристиками или классом точности. Специалист в любой сфере деятельности должен уметь грамотно определять погрешность результатов различных видов измерений, различных измерительных каналов независимо от того, каким способом представлены пределы допускаемых погрешностей средств измерений. Методические указания предназначены для выполнения расчетно-графических работ.
МЕТОДЫ НОРМИРОВАНИЯ ПОГРЕШНОСТИ. КЛАСС ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ
Различные СИ обладают погрешностями, характер проявления которых может быть различным: у одних погрешность аддитивная, у других мультипликативная или нелинейная, а у третьих могут сочетаться все указанные погрешности. Кроме того, у каждого СИ могут наблюдаться случайные и систематические погрешности. Для того чтобы ориентироваться в метрологических свойствах конкретного СИ пользуются так называемыми нормированными значениями погрешности. Под нормированным значением погрешности понимается погрешность, являющаяся предельной для данного типа СИ. При этом как систематическая, так и случайная составляющая погрешности отдельных экземпляров СИ одного и того же типа могут различаться, но в целом для этого типа СИ погрешности не превосходят гарантированного значения. Так нормируются основная и дополнительная погрешности. Именно границы основной погрешности, а также коэффициентов влияния и заносятся в паспорт каждого экземпляра СИ. Вся процедура нормирования СИ основывается на системе стандартов, обеспечивающих единство измерений. Класс точности – это обобщенная метрологическая характеристика СИ, определяемая пределами основной и дополнительной погрешностей. . Классы точности условными обозначениями наносятся на циферблаты, щитки, корпуса СИ, а также указываются в НТД. В связи с большим разнообразием как самих СИ, так и их метрологических характеристик, ГОСТ 8.401-80 устанавливает несколько способов назначения классов точности. При этом в основу заложены следующие положения: - в качестве норм служат пределы допускаемых погрешностей, включающие систематические и случайные составляющие; - основная Первое положение свидетельствует о необходимости разрабатывать СИ с учетом однократного отсчета показаний по величине общей погрешности. Второе положение требует обеспечения максимальной однородности однотипных СИ. Например, можно обеспечить Определяя класс точности, нормируют, прежде всего, пределы допускаемой основной погрешности Классы точности присваиваются СИ при их разработке по результатам государственных приемочных испытаний. Пределы допускаемой основной и дополнительной погрешностей выражают в форме абсолютной, относительной или приведенной погрешности. Если погрешность результатов измерений в данной области принято выражать в единицах измеряемой величины или в делениях шкалы (например, погрешности мер массы или длины), то принимается форма абсолютных погрешностей. Если границы абсолютных погрешностей в пределах диапазона измерений практически постоянны, то принимается форма приведенной погрешности, а если эти границы нельзя считать постоянными, то форма относительной погрешности. Поэтому ГОСТ 8.401-80 в качестве основных устанавливает три вида классов точности СИ. 1. Для пределов допускаемой абсолютной погрешности в единицах измеряемой величины или делениях шкалы. 2. Для пределов допускаемой относительной погрешности в виде ряда чисел
где А = 1; 1,5; (1,6); 2; 2,5; (3); 4; 5; 6, значения 1,6 и 3 допускаемые, но не рекомендуемые; n = 1; 0; -1; -2;… 3.Для пределов допускаемой приведенной погрешности с тем же рядом (1.1)
Абсолютная погрешность может выражаться одним числом Таблица 1.1. Решение. 1. Для СИ класса точности 0,02/0,01. По таблице 1.2 видим, что такое обозначение используется для СИ с установленной относительной погрешностью, при этом она рассчитывается по формуле (1.3), которая имеет вид
отсюда, учитывая, что
Из задания
2. Для СИ с обозначением класса точности. В этом случае из той же таблицы 1.2 имеем формулу (1.2) для расчета относительной погрешности
Таблица 1.2 КАК СЛУЧАЙНЫХ ВЕЛИЧИН Присутствие случайных погрешностей в результатах измерения приводит к тому, что результат измерения является случайной величиной. Поэтому прежде, чем приступить к расчету случайных погрешностей, необходимо ознакомиться с вероятностным описанием случайных величин. Основные понятия.
Случайная величина (СВ) – величина, которая в результате измерения (опыта) может принять то или иное значение, причем неизвестно заранее, какое именно. Дискретная СВ – СВ, принимающая только отделенные друг от друга значения, которые можно заранее перечислить. Например, количество попаданий при 3-х выстрелах, которое может быть равным 0, 1, 2, 3. Их можно заранее перечислить. Непрерывная СВ – СВ, возможные значения которой непрерывно заполняют некоторый конечный или бесконечный интервал. Например, координаты попадания пули в мишень. Случайное событие – событие, которое в результате опыта(измерения, испытания) может произойти или не произойти. Вероятность события - определенное число, отражающее степень объективной возможности этого события. Статистическая совокупность – множество значений СВ, полученное в результате измерений. Генеральная совокупность – статистическая совокупность, содержащая в себе все возможные значения СВ. Выборка – совокупность, содержащая часть значений СВ, принадлежащих генеральной совокупности.
Законы распределения Законом распределения СВ называется любое соотношение, устанавливающее связь между возможными значениями Эта связь может задаваться таблицей, графиком или функциональной зависимостью. Из теории вероятностей известно, что наиболее универсальным способом описания СВ является отыскание их интегральных или дифференциальных функций распределения. Интегральной функцией распределения СВ F(x) (или просто функцией распределения СВ) называется функция, каждое значение которой для каждого
Она имеет следующие свойства. 1. Неотрицательна 2. 3. Неубывающая на всей оси, то есть 4. Вероятность нахождения СВ в диапазоне от
Для иллюстрации этих свойств на рис.2.1,а) показан график интегральной функции распределения нормального (Гауссова) закона. Более наглядным является описание свойств результатов измерений и случайных погрешностей с помощью дифференциальной функции распределения
Функция распределения плотности вероятностей обладает следующими свойствами 1. Неотрицательна, то есть 2. Нормирована Вероятность того, что непрерывная СВ примет некоторое значение из интервала (
Выясним размерности рассмотренных функций. Функция распределения Функция распределения плотности вероятностей имеет размерность обратную размерности СВ. Из уравнения (2.3) следует, что вероятность попадания СВ Выясним размерности рассмотренных функций. Функция распределения Функция распределения плотности вероятностей имеет размерность обратную размерности СВ.
Числовые характеристики СВ
Функции распределения СВ являются самым универсальным способом их описания. Однако, для их определения часто необходимы длительные, объемные и кропотливые исследования и вычисления. Часто бывает достаточно охарактеризовать СВ с помощью числовых характеристик (параметров законов распределения), которые называются моментами различных порядков. Моменты без исключения систематической составляющей называются начальными, а с исключением систематической составляющей (центрированные СВ) центральными. То есть, если усредняются величины, отсчитываемые от начала координат, то моменты называются начальными, а если от центра распределения, то центральными. СВ называется центрированной, если математическое ожидание Начальные моменты еще называют характеристиками положения, таккак они характеризуют форму кривой функции плотности вероятности (математическое ожидание, мода, медиана и др.), а центральные моменты к характеристикам рассеивания (дисперсия, среднеквадратическое отклонение и др.).
Характеристики положения
Как уже упоминалось к этим характеристикам относятся начальные моменты. Начальным моментом
Начальный момент 1-го порядка называется средним арифметическим (для дискретной СВ) или математическим ожиданием (для непрерывной СВ). Обычно обозначается Нулевой начальный момент равен единице и не имеет своего отдельного названия. Он используется для задания условий нормирования функции распределения плотности вероятностей (см. выше). К характеристикам положения относится и понятие центра распределения. Координата центра распределения показывает положение СВ на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, то есть такая точка
Точку Квантилью порядка р (р – процентной квантилью) распределения непрерывной СВ называется действительное число
Например, на рис.2.1.б Величину
В частности, из определения медианы следует, что Можно определить центр распределения, как центр тяжести распределения, то есть такой точки
Это выражение не что иное, как уже упоминавшийся начальный момент первого порядка или математическое ожидание. Необходимо отметить, что у некоторых распределений, например, распределения Коши, не существует математического ожидания, так как определяющий его интеграл расходится. При симметричной кривой Модой непрерывно СВ называется действительное число Существуют распределения, у которых нет моды, например, равномерное. Распределения с одним максимумом называются одномодальными, с двумя – двухмодальными и т.д. Те из них, у которых в средней части расположен не максимум, а минимум, называются антимодальными. Характеристики рассеивания
К этим характеристикам относятся центральные моменты. Центральным моментом
Среди центральных моментов, большое значение имеет второй центральный момент, называемый дисперсий D
и являющийся числовой характеристикой рассевания (мерой рассевания) СВ относительно математического ожидания. Чаще в качестве меры рассеивания используют среднее квадратическое отклонение (СКО)
Оно имеет такую же размерность, как и математическое ожидание, то есть размерность СВ. Для примера на рис. 2.2 показан вид нормального распределения при различных значениях СКО.
Заметим, что математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, так как они определяют важные черты распределений: положение центра и степень разбросанности результатов относительно него. Для более подробного описания распределений используются моменты более высоких порядков. Третий центральный момент
Для симметричных относительно центра распределений он равен нулю. Третий момент имеет размерность куба СВ, поэтому для относительной характеристики асимметрии используют безразмерный коэффициент асимметрии, равный
Четвертый центральный момент
Его относительное значение называется эксцессом распределения
и для разных законов может иметь значения от 1 (для дискретного двузначного) до ∞ (для распределения Коши). Для островершинного треугольного распределения Для удобства используют контрэксцесс, меняющийся для любых распределений от 0 до 1.
Для нормального закона
Нормальное распределение (распределение Гаусса) Нормальное распределение, как и равномерное распределение, является разновидностью экспоненциальных. При этом нормальный закон распределения имеет наибольшее распространение, что объясняется центральной предельной теоремой теории вероятностей, утверждающей, что распределение СВ (погрешностей) будет близко к нормальному всякий раз, когда результаты наблюдений являются суммой большого числа независимых факторов, каждый из которых
оказывает незначительное действие по сравнению с суммарным действием всех остальных. Для нецентрированных СВ это распределение является двухпараметрическим и имеет следующий вид
где Вид нормального распределения был показан на рис.2.2. При введении новой переменной
Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения функций (2.28) и (2.29) сведены в таблицы, которые можно найти в литературе по теории вероятностей. Определенный интеграл с переменным верхним пределом
называют функцией Лапласа. Для нее справедливы следующие равенства:
Функция Лапласа используется для определения значений интегральных функций нормальных распределений. Функция F(t) связана с функцией Лапласа формулой
Поскольку интеграл в (2.30) не выражается через элементарные функции, то значения функции Лапласа для различных значений t сведены в таблицу (см. табл. П 1).
Степенях свободы
Классический аппарат моментов для оценки ширины и формы распределений Стьюдента с малым числом степеней свободы оказывается неработоспособным и их ширина и форма могут быть оценены лишь с использованием доверительных оценок. Этим распределения Стьюдента резко отличаются от всех других рассмотренных ранее законов распределений. По значимости эксцесса (от ε = 3 до ε = ∞) распределения Стьюдента с числом степеней свободы от υ = 4 до υ = ∞ совпадают с распределениями класса экспоненциальных с показателями степени от α = 0 до α = 2. Разновидностью распределения Стьюдента является распределение Коши. Оно важно тем, что ему подчиняется распределение отношения двух нормально распределенных центрированных СВ. Распределение Коши – это предельное распределение семейства законов Стьюдента с минимально возможным числом степеней свободы υ = 1 (рис.2.7). Свойства распределения Коши резко отличаются от свойств экспоненциальных распределений, а именно: - дисперсия и СКО не существуют, так как определяющий их интеграл расходится. Они будут бесконечно увеличиваться при росте числа экспериментальных данных; - оценка центра в виде среднего арифметического для распределения Коши неправомочна, так как ее рассеяние - математическое ожидание не существует; - для определения центра - эксцесс равен бесконечности, контрэксцесс равен нулю.
Значения критерия Шарлье
Вариационный критерий Диксона Кд удобный и достаточно мощный (с малыми вероятностями ошибок). Применяется при числе наблюдений n < 30. При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд Пример 3.2. Было проведено пять измерений напряжения в электросети. Получены следующие результаты: 127,1; 127,2; 126,9; 127,6; 127,2. Результат 127,6В существенно (на первый взгляд) отличается от остальных. Проверить, не является ли он промахом. Решение. Составим вариационный ряд из результатов измерений напряжения в электросети: 126,9; 127,1; 127,2; 127,2; 127,6. Для крайнего члена этого ряда 127,6 критерий Диксона
Кд = (127,6 – 127,2) / (127,6 – 126,9) = 0,4 / 0,7 = 0,57
Как следует из табл.3.3 по этому критерию результат 127,6В может быть отброшен как промах лишь на уровне значимости q = 0,10. Применение рассмотренных критериев требует осмотрительности и учета объективных условий измерения. Оператор должен исключить результат наблюдения с явной грубой погрешностью и выполнить новое измерение. Но нельзя просто отбрасывать более или менее резко отличающиеся от других результаты наблюдений. В сомнительных случаях лучше сделать дополнительные измерения (не взамен сомнительных, а кроме них) и затем использовать рассмотренные критерии. Таблица 3.3 Значения критерия Диксона
Суммирование погрешностей
Суммирование систематических погрешностей. Неисключенная систематическая погрешность результата измерения включает составляющие, обусловленные методом, средствами измерений и другими источниками. Если случайные погрешности малы, то в качестве границ неисключенной систематической погрешности принимают пределы допускаемых основных и дополнительных погрешностей СИ. При суммировании неисключенных систематических погрешностей их рассматривают как случайные величины с равномерным законом распределения. 1. Границы неисключенных систематических погрешностей результата измерения определяются по формуле
где
2. При Р < 0,99 коэффициент k мало зависит от
Таблица 3.4 Косвенные измерения При косвенных измерениях погрешность результата зависит от погрешности каждого из прямых измерений. Результат
Так как каждое Например, пусть При функции Так как возможные функции
Разложим эту функцию в ряд Тейлора
Полагая, что погрешности второго порядка пренебрежимо малы, можем записать
Отсюда, так как
Полученные таким путем значения Аналогично этому, если известны среднеквадратичные отклонения (СКО) случайной абсолютной погрешности
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 531; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.119.119 (0.01 с.) |

 и все виды дополнительных относительных погрешностей
и все виды дополнительных относительных погрешностей 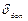 нормируются порознь.
нормируются порознь. за счет любого
за счет любого  . Однако, замена одного СИ другим не всегда будет эквивалентной, поскольку одно СИ может иметь большую температурную погрешность, другое частотную, что при конкретном измерении неизвестно.
. Однако, замена одного СИ другим не всегда будет эквивалентной, поскольку одно СИ может иметь большую температурную погрешность, другое частотную, что при конкретном измерении неизвестно. , (1.1)
, (1.1) .
.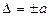 при неизменных границах, двучленом
при неизменных границах, двучленом  – при линейном изменении границ абсолютной погрешности, то есть при совместном проявлении аддитивной и мультипликативной составляющих или в виде графика функции, таблицы при нелинейном изменении границ (например, табл. 1.1).
– при линейном изменении границ абсолютной погрешности, то есть при совместном проявлении аддитивной и мультипликативной составляющих или в виде графика функции, таблицы при нелинейном изменении границ (например, табл. 1.1).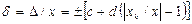 ,
,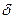 дается в процентах, получим выражение для расчета абсолютной погрешности.
дается в процентах, получим выражение для расчета абсолютной погрешности.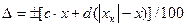 .
.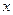 = 25А,
= 25А, 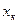 =50А,
=50А, 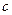 = 0,02,
= 0,02, 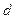 = 0,01, подставляя эти значения, получим
= 0,01, подставляя эти значения, получим
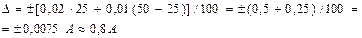
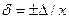 откуда
откуда 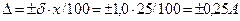
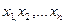 СВ (Х) и соответствующими вероятностями
СВ (Х) и соответствующими вероятностями 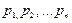 их появления.
их появления.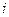 -ом опыте принимает значение
-ом опыте принимает значение 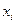 меньше
меньше 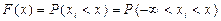 (2.1)
(2.1)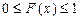 , при
, при 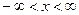
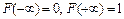 .
.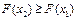 , если
, если 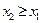 .
.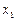 до
до 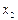
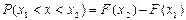 (2.2)
(2.2)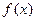 , иначе называемой функцией распределения плотности вероятностей (рис.2.1,б).
, иначе называемой функцией распределения плотности вероятностей (рис.2.1,б).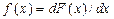 (2.3)
(2.3)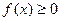 при
при 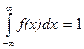 .
.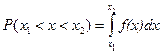 (2.4)
(2.4)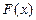 – это вероятность, а поэтому является безразмерной величиной.
– это вероятность, а поэтому является безразмерной величиной.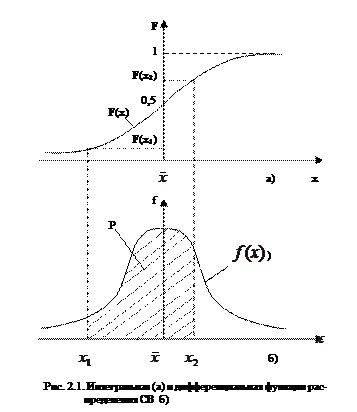
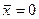 (эту величину рассмотрим ниже).
(эту величину рассмотрим ниже).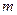 -го порядка (
-го порядка (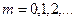 ) распределения СВ называется действительное число
) распределения СВ называется действительное число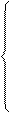
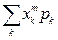 - для дискретных СВ
- для дискретных СВ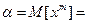 (2.5)
(2.5)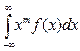 - для непрерывных СВ
- для непрерывных СВ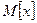 ,
, 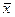 . Будем использовать обозначение
. Будем использовать обозначение 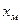 на оси
на оси 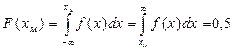 (2.5)
(2.5)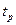 , удовлетворяющее условию
, удовлетворяющее условию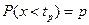 . (2.6)
. (2.6)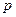 – это выраженная в процентах площадь фигуры, ограниченная сверху кривой
– это выраженная в процентах площадь фигуры, ограниченная сверху кривой 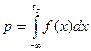 (2.7)
(2.7)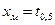 .
.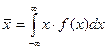 (2.8)
(2.8)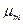 , определяемое по формуле
, определяемое по формуле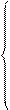
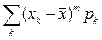 - для дискретных СВ
- для дискретных СВ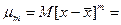 (2.9)
(2.9)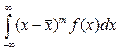 - для непрерывных СВ
- для непрерывных СВ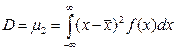 (2.10)
(2.10)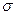
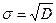 (2.11)
(2.11)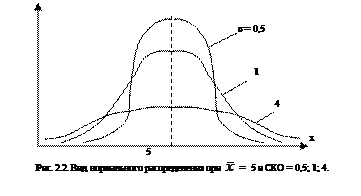
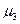 характеризует асимметрию, то есть скошенность распределения: например, когда один спад крутой, а другой пологий
характеризует асимметрию, то есть скошенность распределения: например, когда один спад крутой, а другой пологий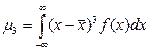 (2.12)
(2.12)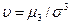 . Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии показан на рис.2.3.
. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии показан на рис.2.3.
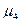 характеризует протяженность распределения, при этом выявляется плоско или островершинность распределения.
характеризует протяженность распределения, при этом выявляется плоско или островершинность распределения.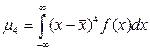 . (2.13)
. (2.13)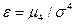 (2.14)
(2.14)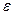 = 2,4, а для кругловершинного нормального
= 2,4, а для кругловершинного нормального 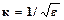 (2.15)
(2.15)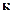 = 0,577
= 0,577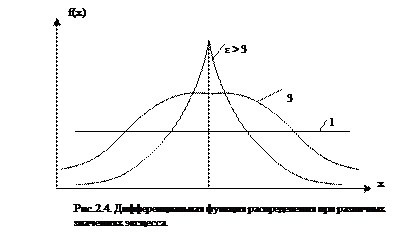
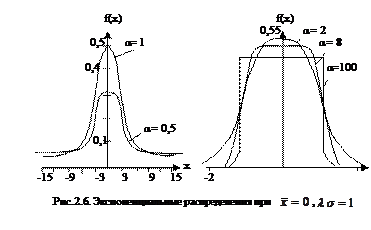
 (2.27)
(2.27) – СКО;
– СКО; 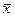 – математическое ожидание.
– математическое ожидание. из (2.27) получается нормированное нормальное распределение, интегральная и дифференциальная функции распределения которого соответственно равны
из (2.27) получается нормированное нормальное распределение, интегральная и дифференциальная функции распределения которого соответственно равны (2.28)
(2.28) (2.29)
(2.29) (2.30)
(2.30) ;
; 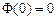 ;
;  ;
; 
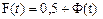 (2.31)
(2.31) равно бесконечности;
равно бесконечности;
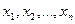
 . Критерий Диксона определяется как
. Критерий Диксона определяется как  Критическая область для этого критерия
Критическая область для этого критерия  . Значения
. Значения  приведены в табл.3.3.
приведены в табл.3.3. , (3.2)
, (3.2) - граница i – й неисключенной систематической погрешности;
- граница i – й неисключенной систематической погрешности; - коэффициент, зависящий от числа слагаемых
- коэффициент, зависящий от числа слагаемых  косвенного измерения определяется расчетом по измеренным значениям
косвенного измерения определяется расчетом по измеренным значениям 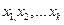 и заранее известной функции
и заранее известной функции (3.15)
(3.15)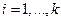 измерено с соответствующей погрешностью
измерено с соответствующей погрешностью  , то задача расчета погрешности
, то задача расчета погрешности  результата
результата  , но
, но 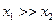 и
и  . В этом случае погрешность в 1%, допущенная при измерении
. В этом случае погрешность в 1%, допущенная при измерении  внесет в результат Z относительную погрешность всего в 0,01%, но такая же погрешность в 1%, допущенная при измерении
внесет в результат Z относительную погрешность всего в 0,01%, но такая же погрешность в 1%, допущенная при измерении  , практически полностью войдет в погрешность результата Z.
, практически полностью войдет в погрешность результата Z.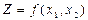 вида
вида  независимо от соотношения между собой
независимо от соотношения между собой  и
и  , погрешность измерения
, погрешность измерения  , а погрешность измерения
, а погрешность измерения 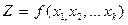 и соотношения
и соотношения  (3.16)
(3.16)
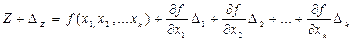
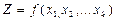 , то
, то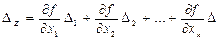
 при данном сочетании
при данном сочетании  можно рассматривать как веса, с которыми в суммарную абсолютную погрешность
можно рассматривать как веса, с которыми в суммарную абсолютную погрешность  входят составляющие в виде абсолютных погрешностей измерения каждого из
входят составляющие в виде абсолютных погрешностей измерения каждого из  , возникающая от абсолютной погрешности
, возникающая от абсолютной погрешности  будет равна
будет равна  .
. отдельных
отдельных 



