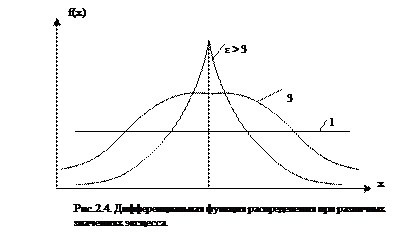Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы вычисления погрешностей и обозначения классов точностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3. Для СИ с обозначением класса точности 1. Из таблицы 1.2 видно, что так обозначаются СИ с нормированной приведенной погрешностью по формуле (1.4)
Пример 1.2. Указатель амперметра с пределами измерений от -10 до 50 А класса точности 1,5 показывает 15А. В каких пределах будет находиться истинное значение силы тока? Решение. Поскольку требуется определить пределы для истинного значения силы тока, то речь идет об абсолютной погрешности. Ее и надо определить. При данном обозначении (см. выше) указана приведенная погрешность γ = 1,5%. Из формулы (1.4) имеем
Нормирующее значение По правилам округления (см. раздел 2.1) Δ = ± 0,8А. При симметричном распределении погрешности измерения результат измерения можно записать I = 15±0,8А или в виде неравенства 14,2 ≤ I ≥ 15,8А. Для СИ, имеющих шкалу с условным нулем (вне пределов измерений)
Пример 1.3. Термоэлектрический термометр класса точности 1 с пределами измерений 300÷1200оС показывает 770 оС. Определить абсолютную и относительную погрешность измерения температуры. Решение. В этом примере при заданном обозначении опять задана приведенная погрешность, рассчитываемая по формуле Относительная погрешность в точке измерения будет равна Тот же результат получим и с использованием формулы (1.5) Если СИ имеет установленное в паспорте номинальное значение, то Пример 1.4. Цифровой частотомер класса точности С показал значение частоты равное 135 кГц. Определить абсолютную погрешность измерения. Решение. Из таблицы 1.2 для СИ класса точности С относительная погрешность рассчитывается по формуле
δ (х) = ± [ 0,02/х + 0,5/100 + х/106] · 100% = =± [ 0,02/135 · 103 + 0,005 + 135 · 103/106] · 100% = 14% δ = ± Δ/х · 100%; Δ = ± х· δ/100% = ±135 · 103 · 14/100 = ±18900Гц = ±18,9 кГц. Отсюда результат измерения f = 135±18,9кГц ≈135±19кГц.
ВЕРОЯТНОСТНОЕ ОПИСАНИЕ ПОГРЕШНОСТЕЙ КАК СЛУЧАЙНЫХ ВЕЛИЧИН Присутствие случайных погрешностей в результатах измерения приводит к тому, что результат измерения является случайной величиной. Поэтому прежде, чем приступить к расчету случайных погрешностей, необходимо ознакомиться с вероятностным описанием случайных величин. Основные понятия.
Случайная величина (СВ) – величина, которая в результате измерения (опыта) может принять то или иное значение, причем неизвестно заранее, какое именно. Дискретная СВ – СВ, принимающая только отделенные друг от друга значения, которые можно заранее перечислить. Например, количество попаданий при 3-х выстрелах, которое может быть равным 0, 1, 2, 3. Их можно заранее перечислить. Непрерывная СВ – СВ, возможные значения которой непрерывно заполняют некоторый конечный или бесконечный интервал. Например, координаты попадания пули в мишень. Случайное событие – событие, которое в результате опыта(измерения, испытания) может произойти или не произойти. Вероятность события - определенное число, отражающее степень объективной возможности этого события. Статистическая совокупность – множество значений СВ, полученное в результате измерений. Генеральная совокупность – статистическая совокупность, содержащая в себе все возможные значения СВ. Выборка – совокупность, содержащая часть значений СВ, принадлежащих генеральной совокупности.
Законы распределения Законом распределения СВ называется любое соотношение, устанавливающее связь между возможными значениями Эта связь может задаваться таблицей, графиком или функциональной зависимостью. Из теории вероятностей известно, что наиболее универсальным способом описания СВ является отыскание их интегральных или дифференциальных функций распределения. Интегральной функцией распределения СВ F(x) (или просто функцией распределения СВ) называется функция, каждое значение которой для каждого
Она имеет следующие свойства. 1. Неотрицательна 2. 3. Неубывающая на всей оси, то есть 4. Вероятность нахождения СВ в диапазоне от
Для иллюстрации этих свойств на рис.2.1,а) показан график интегральной функции распределения нормального (Гауссова) закона. Более наглядным является описание свойств результатов измерений и случайных погрешностей с помощью дифференциальной функции распределения
Функция распределения плотности вероятностей обладает следующими свойствами 1. Неотрицательна, то есть 2. Нормирована Вероятность того, что непрерывная СВ примет некоторое значение из интервала (
Выясним размерности рассмотренных функций. Функция распределения Функция распределения плотности вероятностей имеет размерность обратную размерности СВ. Из уравнения (2.3) следует, что вероятность попадания СВ Выясним размерности рассмотренных функций. Функция распределения Функция распределения плотности вероятностей имеет размерность обратную размерности СВ.
Числовые характеристики СВ
Функции распределения СВ являются самым универсальным способом их описания. Однако, для их определения часто необходимы длительные, объемные и кропотливые исследования и вычисления. Часто бывает достаточно охарактеризовать СВ с помощью числовых характеристик (параметров законов распределения), которые называются моментами различных порядков. Моменты без исключения систематической составляющей называются начальными, а с исключением систематической составляющей (центрированные СВ) центральными. То есть, если усредняются величины, отсчитываемые от начала координат, то моменты называются начальными, а если от центра распределения, то центральными. СВ называется центрированной, если математическое ожидание Начальные моменты еще называют характеристиками положения, таккак они характеризуют форму кривой функции плотности вероятности (математическое ожидание, мода, медиана и др.), а центральные моменты к характеристикам рассеивания (дисперсия, среднеквадратическое отклонение и др.).
Характеристики положения
Как уже упоминалось к этим характеристикам относятся начальные моменты. Начальным моментом
Начальный момент 1-го порядка называется средним арифметическим (для дискретной СВ) или математическим ожиданием (для непрерывной СВ). Обычно обозначается Нулевой начальный момент равен единице и не имеет своего отдельного названия. Он используется для задания условий нормирования функции распределения плотности вероятностей (см. выше). К характеристикам положения относится и понятие центра распределения. Координата центра распределения показывает положение СВ на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, то есть такая точка
Точку Квантилью порядка р (р – процентной квантилью) распределения непрерывной СВ называется действительное число
Например, на рис.2.1.б Величину
В частности, из определения медианы следует, что Можно определить центр распределения, как центр тяжести распределения, то есть такой точки
Это выражение не что иное, как уже упоминавшийся начальный момент первого порядка или математическое ожидание. Необходимо отметить, что у некоторых распределений, например, распределения Коши, не существует математического ожидания, так как определяющий его интеграл расходится. При симметричной кривой Модой непрерывно СВ называется действительное число Существуют распределения, у которых нет моды, например, равномерное. Распределения с одним максимумом называются одномодальными, с двумя – двухмодальными и т.д. Те из них, у которых в средней части расположен не максимум, а минимум, называются антимодальными. Характеристики рассеивания
К этим характеристикам относятся центральные моменты. Центральным моментом
Среди центральных моментов, большое значение имеет второй центральный момент, называемый дисперсий D
и являющийся числовой характеристикой рассевания (мерой рассевания) СВ относительно математического ожидания. Чаще в качестве меры рассеивания используют среднее квадратическое отклонение (СКО)
Оно имеет такую же размерность, как и математическое ожидание, то есть размерность СВ. Для примера на рис. 2.2 показан вид нормального распределения при различных значениях СКО.
Заметим, что математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, так как они определяют важные черты распределений: положение центра и степень разбросанности результатов относительно него. Для более подробного описания распределений используются моменты более высоких порядков. Третий центральный момент
Для симметричных относительно центра распределений он равен нулю. Третий момент имеет размерность куба СВ, поэтому для относительной характеристики асимметрии используют безразмерный коэффициент асимметрии, равный
Четвертый центральный момент
Его относительное значение называется эксцессом распределения
и для разных законов может иметь значения от 1 (для дискретного двузначного) до ∞ (для распределения Коши). Для островершинного треугольного распределения Для удобства используют контрэксцесс, меняющийся для любых распределений от 0 до 1.
Для нормального закона
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.008 с.) |

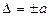
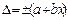
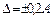
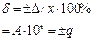
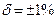
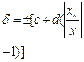
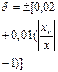
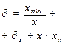
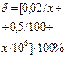
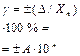
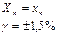

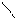 0,5
0,5
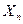 –длина шкалы или ее части,мм
–длина шкалы или ее части,мм
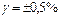
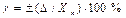 откуда
откуда 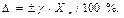
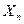 в нашем случае равно 50А, тогда
в нашем случае равно 50А, тогда 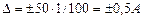
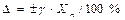
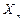 будет равно верхнему пределу измерения
будет равно верхнему пределу измерения 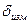 = ±Δ/х = ±9/770·100% = ±1,17%.
= ±Δ/х = ±9/770·100% = ±1,17%.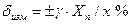 . Действительно
. Действительно 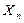 = 50В.
= 50В.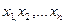 СВ (Х) и соответствующими вероятностями
СВ (Х) и соответствующими вероятностями 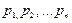 их появления.
их появления.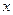 является вероятностью события, заключающегося в том, что СВ Х в
является вероятностью события, заключающегося в том, что СВ Х в 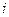 -ом опыте принимает значение
-ом опыте принимает значение 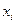 меньше
меньше 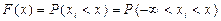 (2.1)
(2.1)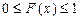 , при
, при 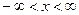
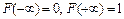 .
.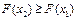 , если
, если 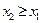 .
.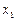 до
до 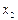
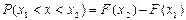 (2.2)
(2.2)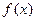 , иначе называемой функцией распределения плотности вероятностей (рис.2.1,б).
, иначе называемой функцией распределения плотности вероятностей (рис.2.1,б).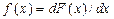 (2.3)
(2.3)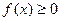 при
при 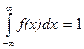 .
.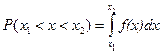 (2.4)
(2.4)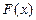 – это вероятность, а поэтому является безразмерной величиной.
– это вероятность, а поэтому является безразмерной величиной.
 (эту величину рассмотрим ниже).
(эту величину рассмотрим ниже). -го порядка (
-го порядка (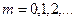 ) распределения СВ называется действительное число
) распределения СВ называется действительное число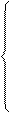
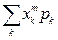 - для дискретных СВ
- для дискретных СВ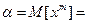 (2.5)
(2.5)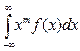 - для непрерывных СВ
- для непрерывных СВ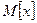 ,
, 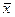 . Будем использовать обозначение
. Будем использовать обозначение 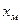 на оси
на оси 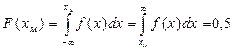 (2.5)
(2.5)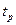 , удовлетворяющее условию
, удовлетворяющее условию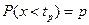 . (2.6)
. (2.6)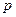 – это выраженная в процентах площадь фигуры, ограниченная сверху кривой
– это выраженная в процентах площадь фигуры, ограниченная сверху кривой 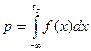 (2.7)
(2.7)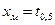 .
.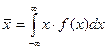 (2.8)
(2.8)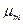 , определяемое по формуле
, определяемое по формуле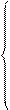
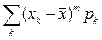 - для дискретных СВ
- для дискретных СВ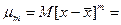 (2.9)
(2.9)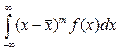 - для непрерывных СВ
- для непрерывных СВ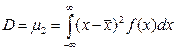 (2.10)
(2.10)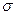
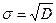 (2.11)
(2.11)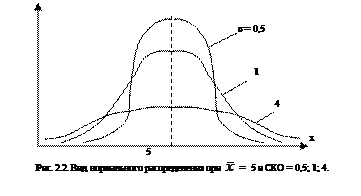
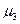 характеризует асимметрию, то есть скошенность распределения: например, когда один спад крутой, а другой пологий
характеризует асимметрию, то есть скошенность распределения: например, когда один спад крутой, а другой пологий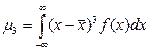 (2.12)
(2.12)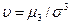 . Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии показан на рис.2.3.
. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии показан на рис.2.3.
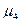 характеризует протяженность распределения, при этом выявляется плоско или островершинность распределения.
характеризует протяженность распределения, при этом выявляется плоско или островершинность распределения.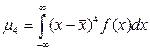 . (2.13)
. (2.13)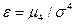 (2.14)
(2.14)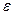 = 2,4, а для кругловершинного нормального
= 2,4, а для кругловершинного нормального 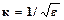 (2.15)
(2.15)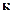 = 0,577
= 0,577