
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значения коэффициента k для различных значений Р и mСодержание книги
Поиск на нашем сайте
3. При Р ³ 0,99 коэффициент k значительно зависит от числа слагаемых m и соотношения между ними. Поэтому при m > 4 рекомендуется принимать среднее значение k = 1,4, а при m £ 4 значение k необходимо уточнить по ГОСТ 8.207-76 или табл.3.5. Параметр С, равный отношению границ составляющих систематической погрешности Таблица 3..5
Значения коэффициента k для различных значений m, C при Р = 0,99
4. При большом числе слагаемых результирующая погрешность имеет практически нормальное распределение. Оценка дисперсии этого распределения равна сумме дисперсий слагаемых
Задавшись доверительной вероятностью, получим Q как границу доверительного интервала Суммирование случайных и систематических погрешностей. Суммарная погрешность результата складывается из случайной составляющей e и неисключенной суммарной систематической погрешности Q. При этом могут возникнуть 3 случая. 1. ∆ = ± e. (3.4) 2. ∆ = ±Q. (3.5) 3.
где При симметричной доверительной вероятности результат измерения представляют в форме
Порядок обработки прямых многократных равноточных измерений
При обработке равноточных результатов измерений обычно исходят из предположения нормального распределения результатов и погрешностей измерений. Если известна систематическая погрешность, то в каждый результат вносят поправку. Если систематическая погрешность постоянна (для равноточных измерений), то ее можно исключить внесением поправки. 1. Исключаются известные систематические погрешности из результатов измерений (статистического ряда):
где
2. Определяется среднее арифметическое значение результатов наблюдений 3. Определяется среднее квадратическое отклонение 4. Выбирается критерий, подходящий условиям измерений (см. п. 3.2.1), проверяется наличие грубых погрешностей и если таковые имеются, то они исключаются из результатов измерений. 5. После исключения грубых погрешностей (если такие обнаружены) повторяются вычисления по пп. 2 и 3. 6. Определяются границы доверительного интервала случайной погрешности результата измерений в соответствии с п.2.5. 7. Определяются границы неисключенной систематической погрешности Q в соответствии с п.3.2.2. 8. Определяются границы доверительного интервала суммарной погрешности в соответствии с п.3.2.2. 9. Записывается окончательный результат измерений.
Многократные прямые неравноточные измерения
При планировании измерений и обработке их результатов часто приходится пользоваться неравноточными измерениями. Неравноточные измерения - это измерения одной и той же физической величины, выполненные с различной точностью, разными приборами, в различных условиях, различными исследователями и т.д. Для оценки наиболее вероятного значения величины по данным неравноточных измерений вводят понятие «веса» измерения:
где Тогда, если неравноточные измерения привели к результатам
Далее расчеты идут аналогично вышеприведенному методу.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.184.124 (0.009 с.) |

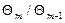 , принимается равным наименьшему значению указанного отношения при условии, что
, принимается равным наименьшему значению указанного отношения при условии, что 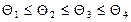 .
.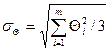 (3.3)
(3.3)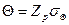 , где
, где 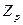 - квантиль нормального распределения при выбранном уровне значимости q = 1 – P.
- квантиль нормального распределения при выбранном уровне значимости q = 1 – P.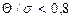 . В этом случае неисключенной систематической погрешностью пренебрегают и в качестве границы погрешности результата измерения принимают
. В этом случае неисключенной систематической погрешностью пренебрегают и в качестве границы погрешности результата измерения принимают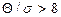 . Пренебрегают случайной составляющей погрешности и принимают
. Пренебрегают случайной составляющей погрешности и принимают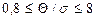 . В этом случае учитывают систематическую и случайную погрешности
. В этом случае учитывают систематическую и случайную погрешности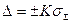 , (3.6)
, (3.6)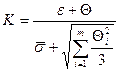 ,
, 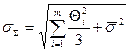 - оценка суммарного СКО суммарной погрешности,
- оценка суммарного СКО суммарной погрешности, 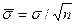 .
.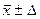 , Р.
, Р.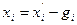 , (3.7)
, (3.7)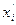 - результат i-го измерения;
- результат i-го измерения;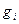 - поправка, определяемая систематической погрешностью;
- поправка, определяемая систематической погрешностью;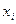 - «исправленный» результат i – го наблюдения.
- «исправленный» результат i – го наблюдения.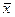 по формуле (2.34).
по формуле (2.34).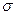 по формуле (2.37).
по формуле (2.37).
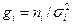 (3.8)
(3.8)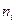 и
и 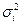 – объем и дисперсия i-й серии равноточных измерений.
– объем и дисперсия i-й серии равноточных измерений.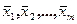 (
(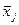 – среднеарифметическое ряда равноточных измерений,
– среднеарифметическое ряда равноточных измерений, 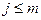 ), то наиболее вероятным значением величины будет ее средневзвешенное значение:
), то наиболее вероятным значением величины будет ее средневзвешенное значение: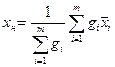 (3.9)
(3.9)


