Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пределы допускаемой абсолютной погрешности вольтметра М-366Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Классы точности СИ, выраженные через абсолютные погрешности, обозначают прописными буквами латинского алфавита или римскими цифрами. При этом, чем дальше буква от начала алфавита, тем больше значение допускаемой абсолютной погрешности. Например, СИ класса С более точен, чем СИ класса М, то есть буква или число это только условное обозначение и не определяет значение погрешности. Класс точности через относительную погрешность СИ назначается двумя способами. 1.Если погрешность СИ имеет в основном мультипликативную составляющую, то пределы допускаемой основной относительной погрешности устанавливают по формуле
Так обозначают классы точности мостов переменного тока, счетчиков электроэнергии, делителей напряжения, измерительных трансформаторов и др. 2. Если СИ имеют как мультипликативную, так и аддитивную составляющие, то класс точности обозначается двумя цифрами, соответствующими значениям
В формуле величина Здесь Формула (1.3) применяется для нормирования погрешности высокоточных СИ: цифровых приборов, многозначных мер сопротивлений и т.п. Наиболее широкое распространение (особенно для аналоговых СИ) получило нормирование класса точности по приведенной погрешности
Условное обозначение класса точности в этом случае зависит от нормирующего значения Если Если Отрицательное влияние аддитивной составляющей погрешности заключается в том, что она не позволяет использовать одно и то же СИ для измерения, как больших, так и малых величин. Поэтому на начальной части шкалы СИ измерения, как правило, недопустимы. Из формулы относительной погрешности
При уменьшении измеряемой величины до значения Тогда, задаваясь некоторым значением относительной погрешности Суммируя вышеизложенное, необходимо сказать, что если класс СИ установлен по наибольшему допускаемому приведенному значению погрешности (формула (1.4)), а для оценки погрешности конкретного измерения необходимо знать значение абсолютной или относительной погрешности в данной точке, то в этом случае выбор СИ, например, класса 1 (γ = 1%) для измерения с относительной погрешностью ±1% будет правильный, если верхний предел В остальных случаях относительную погрешность измерения необходимо определять по формуле
Следовательно, снять показания – не значит измерить. Надо оценить еще и погрешность измерения, учитывая, что случайные погрешности делают результат ненадежным, а систематические – неверным. Для некоторых СИ характерна сложная зависимость относительной погрешности от измеряемой величины или влияющих факторов, которая приводит к логарифмической характеристике точности. ГОСТ 8.401-80 разрешает использовать так называемые специальные формулы нормирования погрешностей для СИ, имеющих более сложные полосы погрешностей. Это, например, цифровые частотомеры, погрешность которых зависит не только от измеряемой величины В этом случае погрешность результатов измерения описывается трехчленной формулой вида
где
Поэтому при измерениях необходимо всегда внимательно изучать документацию на используемые СИ и пользоваться для вычисления погрешности приводимыми в ней формулами. Например, у широкодиапазонного моста сопротивлений в технической документации указано, что относительная погрешность не превосходит значений в диапазонах
102,…, 104 Ом – 0,5% 5,…, 105 Ом – 1% 0,5,…, 106 Ом – 5% 0,2,…, 2 · 106 Ом – 10% 0,1,…, 4 · 106 Ом – 20% Эти данные, как правило, достаточно точно соответствуют трехчленной формуле (1.6). При
Обозначения классов точности в документах и на приборах приведены в табл.1.2.
Решение. 1. Для СИ класса точности 0,02/0,01. По таблице 1.2 видим, что такое обозначение используется для СИ с установленной относительной погрешностью, при этом она рассчитывается по формуле (1.3), которая имеет вид
отсюда, учитывая, что
Из задания
2. Для СИ с обозначением класса точности. В этом случае из той же таблицы 1.2 имеем формулу (1.2) для расчета относительной погрешности
Таблица 1.2
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 756; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

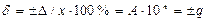 (1.2)
(1.2) Условное обозначение класса точности в этом случае имеет, например, вид, то есть значение δ = ±1%.
Условное обозначение класса точности в этом случае имеет, например, вид, то есть значение δ = ±1%.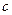 и
и 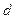 формулы
формулы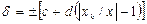 . (1.3)
. (1.3)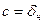 , величина
, величина 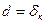 ,
, 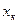 – величина, соответствующая конечному значению шкалы.
– величина, соответствующая конечному значению шкалы.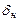 = 0,02%, а к концу
= 0,02%, а к концу 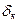 = 0,01%.
= 0,01%.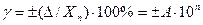 (1.4)
(1.4)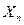 , то есть от шкалы СИ.
, то есть от шкалы СИ.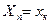 и представляется в единицах измеряемой величины, то класс точности обозначается числом, совпадающим с пределом допускаемой приведенной погрешности. Например, класс 1,5 означает, что γ = 1,5%.
и представляется в единицах измеряемой величины, то класс точности обозначается числом, совпадающим с пределом допускаемой приведенной погрешности. Например, класс 1,5 означает, что γ = 1,5%.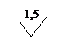 .
.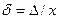 видно, что ее значение растет обратно пропорционально
видно, что ее значение растет обратно пропорционально 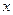 и изменяется по гиперболе, то есть относительная погрешность равна классу СИ лишь на последней отметке шкалы
и изменяется по гиперболе, то есть относительная погрешность равна классу СИ лишь на последней отметке шкалы 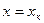 . При
. При 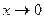 величина
величина 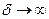 .
.
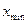 относительная погрешность достигает 100%. Такое значение измеряемой величины называется порогом чувствительности. Эта величина ограничивает снизу полный диапазон
относительная погрешность достигает 100%. Такое значение измеряемой величины называется порогом чувствительности. Эта величина ограничивает снизу полный диапазон 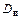 измеряемых величин. Верхняя граница
измеряемых величин. Верхняя граница 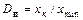 называют еще полным динамическим диапазоном измерения.
называют еще полным динамическим диапазоном измерения.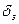 (например,
(например, 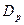 назначается достаточно произвольно.
назначается достаточно произвольно.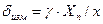 (1.5)
(1.5)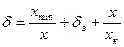 , (1.6)
, (1.6)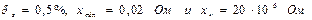 для любого
для любого 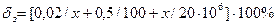
 Пример 1.1. Отсчет по шкале прибора с пределами измерений 0-50 А и равномерной шкалой составил 25 А. Пренебрегая другими видами погрешностей измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ и обозначений класса точности: 0,02/0,01; и 1.
Пример 1.1. Отсчет по шкале прибора с пределами измерений 0-50 А и равномерной шкалой составил 25 А. Пренебрегая другими видами погрешностей измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ и обозначений класса точности: 0,02/0,01; и 1.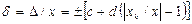 ,
,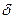 дается в процентах, получим выражение для расчета абсолютной погрешности.
дается в процентах, получим выражение для расчета абсолютной погрешности.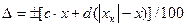 .
.
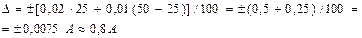
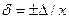 откуда
откуда