
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение погрешности средств измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Точность измерений – качество измерений, отражающее близость их результатов к истинному значению измеряемой величины. На практике для характеристики точности измерений пользуются термином «погрешность измерений». Погрешность результата измерения - это разница между результатом измерения хизм и истинным значением хист измеряемой величины:
Погрешности СИ классифицируют, в частности, по следующим признакам: По способу выражения. Абсолютная погрешность измерительного прибора - разность между показанием прибора и действительным значением измеряемой величины или выраженную в тех же единицах, что и измеряемая величина. Δ х = х – хи
Пример: 0,4 В; 2,5 мкм. Абсолютная погрешность, взятая с обратным знаком, называется поправкой измерительного прибора. Относительная погрешность измерительного прибора - отношение абсолютной погрешности прибора к действительному значению величины, выраженное в процентах. Приведенная погрешность прибора — отношение (в процентах) абсолютной погрешности прибора к нормирующему значению ух = Для приборов, шкала которых содержит нулевую отметку, в качестве нормирующего значения принимают размах шкалы прибора Например, если прибор имеет шкалу от 0 до 1000 единиц, то хN =|1000 - 0| = 1000 ед. В зависимости от условий измерений (по характеру изменения ФВ). Статической называют погрешность, не зависящую от скорости изменения измеряемой величины во времени. Динамической называют погрешность, зависящую от скорости изменения измеряемой величины во времени. 3. По влиянию внешних условий различают: Основной называется погрешность средства измерений, определяемая в нормальных условиях его применения. Для каждого средства измерений в нормативно-технических документах оговариваются условия эксплуатации - совокупность влияющих величин (температура окружающей среды, влажность, давление, напряжение, частота питающей сети и др.), при которых нормируется его погрешность (влияющая величина - это физическая величина, не измеряемая данным средством измерений, но оказывающая влияние на его результаты). Дополнительной называется погрешность средства измерений, возникающая вследствие отклонения какой-либо из влияющих величин, т.е. дополнительная погрешность, увеличивающая общую погрешность прибора, возникает, если прибор работает в условиях, отличных от нормальных (дополнительная температурная погрешность). 4. По характеру изменения результатов при повторных измерениях.. Суммарная погрешность измерения складывается под влиянием большого количества факторов из систематической и случайной составляющих. Случайной погрешностью измерения называют составляющую суммарной погрешности измерения, определяемую действием нерегулярно проявляющихся факторов, неожиданно исчезающих или появляющихся с интенсивностью, которую трудно предвидеть, например перекосы элементов приборов, нерегулярные изменения моментов трения в опорах, флуктуации влияющих величин, изменения внимания операторов и др. Ее отличительная особенность состоит в том, что она случайно изменяется при повторных измерениях одной и той же величины. Пример: при измерении валика одни и тем же прибором в одном и том же сечении получаются различные значения измеренной величины. Во многих случаях влияние случайных погрешностей можно уменьшить путем выполнения многократных измерений с последующей статистической обработкой полученных результатов. Систематической погрешностью измерения называют составляющие суммарной погрешности, определяемые действием постоянных или закономерно изменяющихся факторов в процессе измерительного эксперимента, например плавных изменений влияющих величин или погрешностей применяемых при измерениях образцовых мер. Пример: настройка прибора во времени. Систематические подразделяются на постоянные, прогрессивные (износ наконечников, контактирующих с деталью при контроле ее прибором активного контроля) и периодические (перемещение указателя измерительного прибора). Грубые погрешности (промахи) — это погрешности, связанные с человеческим фактором, например вызванные неправильным обращением наблюдателя со средствами измерений, неверным отсчетом показаний или ошибками при регистрации результатов. Такие погрешности нельзя скорректировать, например падение напряжения в сети электропитания. В некоторых случаях оказывается, что результат одного измерения резко отличается от результатов других измерений, выполненных при тех же контролируемых условиях. По причине возникновения. Инструментальные погрешности измерений — это погрешности применяемых средств измерений. Пример: помехи на входе СИ, вызываемые его подключением к объекту измерений. Методическая погрешность — погрешность за счет либо неточного описания модели физического процесса, на основе которых строятся средства измерений, либо неправильного процесса эксплуатации. Например, измерение температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима объекта измерения вследствие внесения термопары; при измерениях параметров электрических цепей (сопротивлений, емкостей); при измерении давления газа в замкнутом сосуде с помощью мембранных (сильфонных) преобразователей давления возникает погрешность, вызываемая прогибом мембраны под действием давления: при этом изменяется объем сосуда и давление. Субъективная погрешность — погрешность, связанная с квалификацией оператора и его психологическим состоянием, а также с несовершенством зрительной системы человека. В большинстве случаев они относятся к случайным, но могут быть и систематическими. Во многих случаях систематическую погрешность в целом можно представить как сумму двух составляющих аддитивной Dа и мультипликативной Dм. Аддитивная погрешность - погрешность, которая искажает результат за счет арифметического суммирования и не зависит от абсолютного значения измеряемой величины. Абсолютные аддитивные погрешности не зависят от чувствительности измерительного прибора и постоянны для всего диапазона измерений. От значений абсолютной аддитивной погрешности зависит наименьшее значение величины, которое может быть определено измерительным прибором. Мультипликативная погрешность - погрешность, которая изменяется с изменением значений измеряемых величин, например при изменении чувствительности средства измерения. Мультипликативные погрешности пропорциональны значению измеряемой величины и чувствительности прибора. Источники мультипликативной погрешности - действие влияющих величин на параметры элементов и узлов средств измерений. Класс точности средства измерений – обобщенная характеристика средства измерений, определяемая пределами допускаемых основных и дополнительных погрешностей. Класс точности выбирается из ряда (0,1, 0,5, 1; 1,5; 2; 2,5; 4; 5; 6)*10n, где n = 1; 0; -1; -2 и т. д. Класс точности может выражаться одним числом или дробью (если аддитивная и мультипликативная погрешности сопоставимы – например, 0,2/0,05 – адд./мульт.). Примеры обозначения классов точности на средстве измерения.
Допускаемой погрешностью считается погрешность прибора, при которой он может быть признан годным и допущен к применению. Пределы допускаемой основной погрешности, которые выражают в форме приведенной или относительной погрешности, обозначаются числами, равными этим пределам в процентах. Для того чтобы отличить от приведенной относительную погрешность — класс точности, его обозначение обводят кружком. Если погрешность нормирована в процентах от длины шкалы, то под обозначением класса ставится знак точности. Например, под шкалой амперметра с пределами измерения 0...10 А нанесено обозначение класса точности 2,5. Следовательно, нормированная приведенная погрешность этого прибора 2,5. Если Хн = 10 А и р = 2,5, то
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 2388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.202 (0.012 с.) |

 .
. х – хд.
х – хд.
 .
.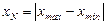 .
. где Хн - нормирующее значение, выраженное в тех же единицах, что и х; р - отвлеченное положительное число, выбираемое из стандартизованного ряда значений (1∙10n, 1,5∙10n, 5∙10n, где n = -1, 0, -1,-2,..., -10 и т.д.).
где Хн - нормирующее значение, выраженное в тех же единицах, что и х; р - отвлеченное положительное число, выбираемое из стандартизованного ряда значений (1∙10n, 1,5∙10n, 5∙10n, где n = -1, 0, -1,-2,..., -10 и т.д.).

 0,5
0,5
 где q - отвлеченное положительное число, выбираемое из стандартизованного ряда значений; с, d - положительные числа, выбираемые из стандартизованного ряда; Хk - больший по модулю предел измерений (верхний предел измерения или сумма пределов измерения для приборов с нулем посередине шкалы); х - показание прибора.
где q - отвлеченное положительное число, выбираемое из стандартизованного ряда значений; с, d - положительные числа, выбираемые из стандартизованного ряда; Хk - больший по модулю предел измерений (верхний предел измерения или сумма пределов измерения для приборов с нулем посередине шкалы); х - показание прибора.





