
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка точности геодезических измерений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Лекция 3. Оценка точности геодезических измерений.
1. Виды измерений. Виды погрешностей измерений. Свойства случайных погрешностей. 2. Меры точности равноточных измерений. Арифметическая середина и оценка её точности. Средние квадратические погрешности функций измеренных величин. 3. Неравноточные измерения.
Виды измерений.
Измерить какую-либо величину — значит сравнить её с однородной ей величиной, принятой за единицу меры. Результат измерений есть число, показывающее, сколько раз единица меры содержится в измеряемой величине, при этом число может быть целым и дробным. Виды измерений: - прямые и косвенные; - необходимые и избыточные; - равноточные и неравноточные. Прямые – если измеряется непосредственно какая-либо величина; искомый результат получается прямо из измерений.
Косвенные — если значение искомой величины, находится вычислением на основании непосредственно измеренных величин.
Необходимые — измерения, дающие одно значение измеряемой величины.
Бесконтрольное измерение Избыточные — все n измерений одной величины, кроме одного, т.е. п-1. Избыточные измерения не следует смешивать с понятием «излишние измерения» они обязательны. Необходимы для контроля измерений и повышения надёжности значения искомой величины.
Равноточные — измерения, выполненные в одинаковых условиях, а поэтому имеют практически одинаковую точность. Условия: - прибор - способ измерения - число измерений (приёмов) - квалификация наблюдателя - внешние условия. Неравноточные — измерения, выполненные в одинаковых условиях, а поэтому имеющие
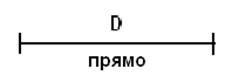
Виды погрешностей измерений. Свойства случайных погрешностей. Любое измерение сопровождается погрешностью. Погрешность результата измерений — это разность между измеренным и истинным (точным) значением определяемой величины. (это разность между тем, что есть и тем, что должно быть). Виды погрешностей: - грубые; - систематические; - случайные. Грубые — погрешности, величина которых совершенно недопустима при данных условиях измерений. Возникают вследствие просчётов, промахов, например: - просчёт количества отложений мерной ленты при измерении расстояний; - просчёт при покупках на 1, 10 руб. Грубые ошибки выявляются и устраняются избыточными измерениями. Систематические - погрешности, которые входят в каждый результат по определённому закону. Могут подразделяться на: - постоянные по знаку и величине; - переменные по знаку и величине. Примеры: — измеряется расстояние (линия L) лентой длиной L=20м., которой больше или меньше на величину
Конечный результат измерения будет отличаться на величину.
где L –длина линии.
- длина ленты проверялась при температуре

Причины появления систематических ошибок необходимо изучать в каждом отдельном случае. Влияние их на результат измерения должен исключаться или сводится к минимуму путём введения поправок в результат измерения.
Случайные — погрешности, возникновение которых не удаётся подчинить определённым законом. Случайные погрешности неизбежны. Источники случайных ошибок: - прибор - наблюдатель - внешние условия. Уменьшение влияния случайных ошибок может быть достигнуто совершенствованием приборов, повышением квалификации.
Обозначения:
- точное (истинное) значение величин Х - измеренное значение величин l - случайная погрешность
или Если l >Х то (+
В процессе геодезических измерений точность снятия отсчётов угломерных, мерных (линейных) выше точности результата измерений, следовательно, имеет место равномерное распределение случайных погрешностей.
График функции плотности вероятного нормального распределения случайных погрешностей. (Кривая Гаусса).
Свойства случайных погрешностей равноточных измерений
Анализ большого ряда измерений позволил установить следующие (4) свойства случайных погрешностей. 1. Свойство ограниченности Случайные погрешности по абсолютной величине не могут превышать определённого предела, т.е. переходят в разряд грубых погрешностей.
2. Свойство симметрии Равные по абсолютной величине положительные и отрицательные случайные
3. Свойство компенсации Среднее арифметическое из случайных погрешностей равноточных измерений одной и той же величины стремится к нулю при возрастании числа измерений. Это свойство можно выразить математически
где [ ] — знак суммы введённый Гауссом.
4. Свойство плотности Малые по абсолютной величине погрешности встречаются чаще, чем большие.
На основании этих свойств основаны: - способы оценки точности результатов измерений - служат основой для определения наиболее надёжных значений измеряемой величины. 2.Мерыточности равноточных измерений.
О точности измерений можно приблизительно судить по рассеиванию (разбросу) результатов измерений, чем больше расходятся между собой результаты измерений, тем ниже точность измерений. Основными мерами (характеристиками) точности измерений в геодезии являются: — средняя квадратическая погрешность; — предельная погрешность; — относительная погрешность. Средняя погрешность — среднее арифметическое из абсолютных величин
где
Пример Имеем два ряда погрешностей
I ряд: -1; +2; -6; +7; -1; [ II ряд: -4;+2; -4;+3; -4; [ Средняя погрешность отдельного измерения будет равна: для I ряда для II ряда Анализ: — средние погрешности этих рядов одинаковы; 6
— отдельные случайные погрешности в 1 ряду крупнее случайных погрешностей второго ряда; — крупные погрешности снижают точность измерений. Следовательно, средняя погрешность недостаточно чувствительна к крупным погрешностям, она сглаживает их влияние. Вывод, 1)Точность вычисления С.К.П. в этом случае достигает 25% от её величины. 2)При восьми измерениях можно получить надёжный результат вычислений по формуле.
3)Для более точных измерений углов необходимо использовать теодолиты большей
3. По величине С.К.П. можно определить предельную погрешность В теории вероятностей доказывается, что при достаточно большом числе измерений
— больше Зm в 3 случаях из 1000 измерений.
Поэтому можно принять
2m— устанавливают при высокоточных измерениях 3m — в остальных случаях. Выводы: 1)Исходя, из указанных достоинств С.К.П. принимается для оценки геодезических измерений в качестве основной меры точности. 2)Характеризуя точность измерения С.К.П. (m), необходимо также указывать и С.К.П. (
3)Числовые значения средней, С.К.П., и предельной погрешности достаточно вычислять до двух значащих цифр. (т =
4)Среднюю С.К.П.,
Относительная погрешность Рассмотрим результаты измерений двух линий:
Рассмотрим: а) абсолютные погрешности измерений: - 1-я линия измерена точнее, чем вторая, т.к. б) вторая линия длиннее первой и очевидно погрешность измерения линии будет зависеть от её длины. Поэтому для оценки точности длин линий пользуются относительной погрешностью. Относительную погрешность обычно представляют дробью, числитель которой равен 1, а
Оценка измерений длин линий.
- вторая линия измерена точнее первой, хотя - относительные погрешности не применяют при оценке точности угловых измерений,
Функций измеренных величин. В практике измерений, часто приходится пользоваться величинами, которые не измеряются, а определяются на основании измеренных величин, т.е, являются некоторыми функциями. Во всех таких случаях возникает задача вычислений С.К.П. функций, по известным С.К.П. измеренных величин (аргументов). 1)Дано U=х+у погрешности аргументов
если каждый аргумент измерялся n раз.
…………………….
возведем равенства в квадрат и просуммируем
Разделив обе части на n
Рассуждая аналогично, можно показать, что выражение 2) U=
обозначив
З.Неравноточные измерения. Измерения, выполненные с различной точностью, в различных условиях. Степень надёжности результатов измерений выражают числом, называемым весом этого результата.
ЧЕМ НАДЕЖНЕЕ РЕЗУЛЬТАТ, ТЕМ БОЛЬШЕ ЕГО ВЕС. Следовательно, вес связан с точностью результат измерений, которая характеризуется С.К.П. Поэтому вес результата измерений принимают равным величине обратно
где: -р- вес результата измерений; -с- произвольное, но одно и тоже число при вычислении всех весов в данной задаче Веса результатов измерений
Для облегчения задачи отыскания весов обычно вес одного из результатов с погрешностью
тогда веса результатов наблюдений
Окончательный (наиболее точный) результат неравноточных измерений равен сумме произведений каждого из этих измерений на его вес делённый на сумму весов всех измерений.
арифметической середины. Кроме того, необходимо найти: - уклонения
- С.К.П. единицы веса по формуле Бесселя
- С.К.П. общей арифметической середины
-С.К.П. определения самой средней квадратической погрешности М
Лекция 3. Оценка точности геодезических измерений.
1. Виды измерений. Виды погрешностей измерений. Свойства случайных погрешностей. 2. Меры точности равноточных измерений. Арифметическая середина и оценка её точности. Средние квадратические погрешности функций измеренных величин. 3. Неравноточные измерения.
Виды измерений.
Измерить какую-либо величину — значит сравнить её с однородной ей величиной, принятой за единицу меры. Результат измерений есть число, показывающее, сколько раз единица меры содержится в измеряемой величине, при этом число может быть целым и дробным. Виды измерений: - прямые и косвенные; - необходимые и избыточные; - равноточные и неравноточные. Прямые – если измеряется непосредственно какая-либо величина; искомый результат получается прямо из измерений.
Косвенные — если значение искомой величины, находится вычислением на основании непосредственно измеренных величин.
Необходимые — измерения, дающие одно значение измеряемой величины.
Бесконтрольное измерение Избыточные — все n измерений одной величины, кроме одного, т.е. п-1. Избыточные измерения не следует смешивать с понятием «излишние измерения» они обязательны. Необходимы для контроля измерений и повышения надёжности значения искомой величины.
Равноточные — измерения, выполненные в одинаковых условиях, а поэтому имеют практически одинаковую точность. Условия: - прибор - способ измерения - число измерений (приёмов) - квалификация наблюдателя - внешние условия. Неравноточные — измерения, выполненные в одинаковых условиях, а поэтому имеющие
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 3139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |







 ;
;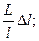


 ,а измерения проводятся при температуре t. Результат измерений будет содержать погрешность пропорциональную разности температур и длине линии.
,а измерения проводятся при температуре t. Результат измерений будет содержать погрешность пропорциональную разности температур и длине линии.








 (тэта)
(тэта) - абсолютное значение случайной погрешности
- абсолютное значение случайной погрешности 


 , которая может иметь при данных условиях измерений.
, которая может иметь при данных условиях измерений. с вероят. 0,950
с вероят. 0,950 с вероят. 0,0997
с вероят. 0,0997 или
или  ) вычисления С.К.П.
) вычисления С.К.П.
 0,35 или т =
0,35 или т =  погрешность называют абсолютными погрешностями, т.к. на их значение не влияет величина измеряемой величины.
погрешность называют абсолютными погрешностями, т.к. на их значение не влияет величина измеряемой величины. = 350,10м.
= 350,10м.  0,35м.
0,35м. = 800,25м.
= 800,25м.  0,40м.
0,40м.

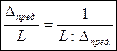

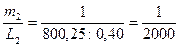
 и
и 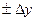









 т.к.
т.к. 
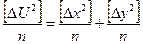 согласно
согласно 
 -С.К.П. функции и аргументов.
-С.К.П. функции и аргументов. справедливо и для функции u=x-y, а если
справедливо и для функции u=x-y, а если  то
то  .
.
 то
то  на основании
на основании 


 , если
, если 

 ,
,
 (мю) принимают за единицу и относительно его вычисляют веса
(мю) принимают за единицу и относительно его вычисляют веса  откуда с =
откуда с = 

 — формула весового среднего или общей
— формула весового среднего или общей от измеренных величин
от измеренных величин






