
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя квадратическая погрешность (С.К.П.)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формулу для её определения разработал К.Ф.Гаусс.
где n — число измерений. С.К.П. является надёжной мерой точности, так как она обладает тремя достоинствами:
На величину С.К.П. сильное влияние оказывают большие по величине погрешности, которые по существу и определяют качество измерений. Для примера случайных ошибок I и II ряда:
С.К.П. является устойчивым критерием для оценки точности измерений.
при n=4 n=8 n=50 n=100
Вывод, 1)Точность вычисления С.К.П. в этом случае достигает 25% от её величины. 2)При восьми измерениях можно получить надёжный результат вычислений по формуле.
3)Для более точных измерений углов необходимо использовать теодолиты большей
3. По величине С.К.П. можно определить предельную погрешность В теории вероятностей доказывается, что при достаточно большом числе измерений
— больше Зm в 3 случаях из 1000 измерений.
Поэтому можно принять
2m— устанавливают при высокоточных измерениях 3m — в остальных случаях. Выводы: 1)Исходя, из указанных достоинств С.К.П. принимается для оценки геодезических измерений в качестве основной меры точности. 2)Характеризуя точность измерения С.К.П. (m), необходимо также указывать и С.К.П. (
3)Числовые значения средней, С.К.П., и предельной погрешности достаточно вычислять до двух значащих цифр. (т =
4)Среднюю С.К.П.,
Относительная погрешность Рассмотрим результаты измерений двух линий:
Рассмотрим: а) абсолютные погрешности измерений: - 1-я линия измерена точнее, чем вторая, т.к.
б) вторая линия длиннее первой и очевидно погрешность измерения линии будет зависеть от её длины. Поэтому для оценки точности длин линий пользуются относительной погрешностью. Относительную погрешность обычно представляют дробью, числитель которой равен 1, а
Оценка измерений длин линий.
- вторая линия измерена точнее первой, хотя - относительные погрешности не применяют при оценке точности угловых измерений,
Арифметическая середина и оценка её точности. Имеется ряд равноточных измерений величины и её истинное значение, т.е.: - Согласно определению случайной погрешности
………….
Величина
Вывод. 1)Так согласно 3-го свойства случайных погрешностей равноточных измерений
2)На практике выполняют небольшое количество измерений. Тем не менее,и в этих случаях принято считать арифметическую середину из равноточных измерений наиболее надёжным результатом таких измерений. Отклонения, или вероятнейшие погрешности. Поэтому случайные погрешности
а значит не может быть вычислена и С.К.П. отдельного измерения по формуле
Тогда оценку точности измерений проводят по отклонениям или вероятнейшим погрешностям отдельных измерений от арифметической середины:
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.180.158 (0.008 с.) |



 - квадрат случайной погрешности
- квадрат случайной погрешности

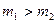
 и m
и m 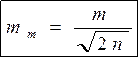 В теории оценки измерений выводится приближённая формула для определения точности вычисления С. К. П.
В теории оценки измерений выводится приближённая формула для определения точности вычисления С. К. П. 36%
36% 25%
25% 1%
1% 0,1%
0,1% , которая может иметь при данных условиях измерений.
, которая может иметь при данных условиях измерений. с вероят. 0,950
с вероят. 0,950 с вероят. 0,0997
с вероят. 0,0997
 или
или  ) вычисления С.К.П.
) вычисления С.К.П.
 0,35 или т =
0,35 или т =  погрешность называют абсолютными погрешностями, т.к. на их значение не влияет величина измеряемой величины.
погрешность называют абсолютными погрешностями, т.к. на их значение не влияет величина измеряемой величины. = 350,10м.
= 350,10м.  0,35м.
0,35м. = 800,25м.
= 800,25м.  0,40м.
0,40м.

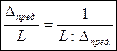

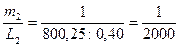
 - Х.
- Х. =1-Х) или (1-Х=
=1-Х) или (1-Х= 
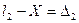

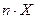 = [
= [ 

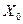 является арифметической серединой или средним арифметическим из результатов измерений l, тогда
является арифметической серединой или средним арифметическим из результатов измерений l, тогда или
или 
 , то арифметическая середина стремится к истинному значению при возрастании числа измерений
, то арифметическая середина стремится к истинному значению при возрастании числа измерений 
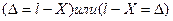 ,
,



