
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация погрешностей измерений. Правила округления результатов измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Степень приближения результата измерения к истинному значению определяется размером погрешности (разностью между полученным при измерении и истинным значениями величины), т. е. качество измерений характеризуется их погрешностями. Поскольку истинное значение измеряемой величины остается неизвестным, неизвестны также и погрешности измерения. Поэтому для определения размеров погрешностей используют условно-истинное значение физической величины, полученное, как правило, в результате более точных измерений или другими методами. Единицы физических величин воспроизводятся с высокой точностью с помощью государственных первичных эталонов и передаются «вниз» эталонным средствам измерений, а от них — рабочим средствам измерений с некоторой потерей точности на каждой ступени передачи (при каждой поверке). При этом значение величины, воспроизводимой эталонным средством измерения при поверке, всегда принимается в качестве условно-истинного значения величины и по нему оценивается погрешность поверяемого средства измерений. Изучение причин возникновения погрешностей и уменьшение размеров погрешностей — одна из главных задач практической метрологии, поэтому понятие «погрешность» — одно из центральных в метрологии. В зависимости от причин и места возникновения погрешности подразделяют на следующие группы: инструментальные, методические, субъективные. Инструментальная погрешность — это погрешность применяемого средства измерения. Если применяется стандартное СИ, прошедшее поверку, то интервал, в котором находится эта погрешность, известен с заданной вероятностью. Методическая погрешность обусловлена несовершенством применяемого метода измерения. На ее величину оказывают влияние несовершенство принятой измерительной модели, способ применения измерительного средства, алгоритмы, по которым вычисляют результат измерения и другие факторы, не связанные со свойствами применяемого измерительного средства. Методическая погрешность не может быть указана в нормативно-технической документации на используемое средство измерений, так как от него не зависит, и должна определяться в каждом конкретном случае путем специальных исследований (анализа измерительной схемы). Несовершенство применяемого метода измерений (неправильная оценка возникающей методической погрешности) неоднократно приводило к ошибочным выводам при проведении научно-исследовательских работ. Например, для оценки внутренних напряжений в твердеющем бетоне использовали мембранные датчики с деформативностью, в несколько раз превышающей деформативность бетона. В результате фактически измеряли не наибольшее внутреннее давление, а остаточное давление на контакте с мембраной после ее деформации.
Субъективная погрешность (погрешность оператора) обусловлена недостаточной квалификацией или индивидуальными особенностями оператора, выполняющего измерения, и связана с тщательностью выполнения правил всех измерительных операций. Эта погрешность не всегда поддается правильной оценке. В отдельную группу выделяют погрешности, обусловленные влиянием внешних условий. Температура, влажность, давление и другие факторы влияют на размеры инструментальной и методической погрешностей. При этом дополнительная инструментальная погрешность, вызываемая отклонением от нормальных условий какого-либо влияющего фактора, может быть указана в метрологических характеристиках средств измерений (в дополнение к основной, определяемой при нормальных условиях). Влияние внешних факторов на методическую погрешность следует оценивать отдельно в каждом конкретном случае. Для большинства видов измерений наиболее полно изучено и поддается учету при определении погрешностей влияние температуры окружающей среды. Погрешности внешних условий по характеру проявления являются систематическими. Под влиянием совокупности всех действующих факторов, в том числе внешних, складывается суммарная погрешность измерения. Влияние каждого фактора может исследоваться отдельно, но удобно для исследования и оценки погрешностей делить суммарную погрешность на две составляющие: случайную и систематическую, принципиально отличающиеся по характеру проявления: и требующие применения различных способов для их обнаружения, оценки и учета. Случайная погрешность — составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера физической величины, проведенных с одинаковой тщательностью в одних и тех же условиях. В появлениях таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов (рис. 3.1). Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результатах измерений. Описание случайных погрешностей возможно только на основе теории вероятностей и математической статистики.
Рис. 3.1. Изменение случайной погрешности при многократных измерениях: х — значения измеряемой величины;
В отличие от систематических случайные погрешности нельзя исключить из результатов измерений путем введения поправок. Однако их можно существенно уменьшить путем увеличения числа измерений, поскольку среднее арифметическое значение х при этом стремится к истинному значению измеряемой величины Q. Систематическая погрешность — составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же физической величины. На рис. 3.2 приведены результаты многократных измерений, содержащих случайную и систематическую погрешности. Систематическая погрешность, как правило, не изменяется при многократных измерениях и может быть почти полностью устранена путем обнаружения и устранения причины, по которой она возникла, или путем введения поправки ( Следует считать, очевидно, что ряд систематических по своей природе погрешностей присутствует при измерениях в скрытом виде. Они не обнаружены или не изучены. Поэтому не всегда удается четко разделить погрешности на систематические и случайные.
х — значения измеряемой величины;
Часть систематических погрешностей, трудно поддающихся учету, причисляют к случайным. Чем больше результаты измерения искажены неучтенными систематическими погрешностями, тем труднее они поддаются математической обработке. Сказанное в определенной мере объясняет те дискуссии, которые ведутся в последние годы вокруг нового понятия «неопределенность измерений». При измерениях могут появляться также очень большие грубые погрешности (промахи), которые возникают, как правило, из-за ошибок или неправильных действий оператора, а также из-за кратковременных отказов или сбоев в работе измерительных приборов и других резких изменений условий проведения измерений. Грубые погрешности обнаруживают и отбрасывают непосредственно в процессе измерений или при математической обработке результатов измерений с использованием специальных критериев.
Погрешность результата измерения физической величины дает представление о том, какие последние цифры в его числовом значении являются сомнительными. Поэтому нет смысла выражать погрешность более чем одной или двумя цифрами. В соответствии с установленными правилами погрешность выражается двумя значащими цифрами, если первая из них 1 или 2, и одной, начиная с цифры 3. Числовое значение результата измерения также следует округлять в соответствии с числовым разрядом значащей цифры по грешности, т. е. числовое значение результата измерения должно оканчиваться цифрой того же разряда или тем же десятичным знаком, которым оканчивается значение абсолютной погрешности. При этом, если старшая отбрасываемая цифра меньше 5, то предыдущая не изменяется. Если старшая отбрасываемая цифра больше или равна 5, но за ней имеются значащие цифры, то предыдущую (оставляемую) цифру увеличивают на единицу. Если отбрасываемая цифра 5 не имеет за собой значащих цифр, то предыдущая не изменяется, если она четная, и увеличивается на единицу, если она нечетная. Например, при погрешности ±0,01 приведенные результаты округляются следующим образом: 1,214 - 1,21; 1,2151 - 1,22; 1,215 - 1,22; 1,225 - 1,22. Следует осмотрительно относиться к округлениям, производимым в процессе вычислений. Рекомендуется производить округления в окончательном ответе, а вычисление производить с одним-двумя лишними знаками.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 790; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.240 (0.009 с.) |

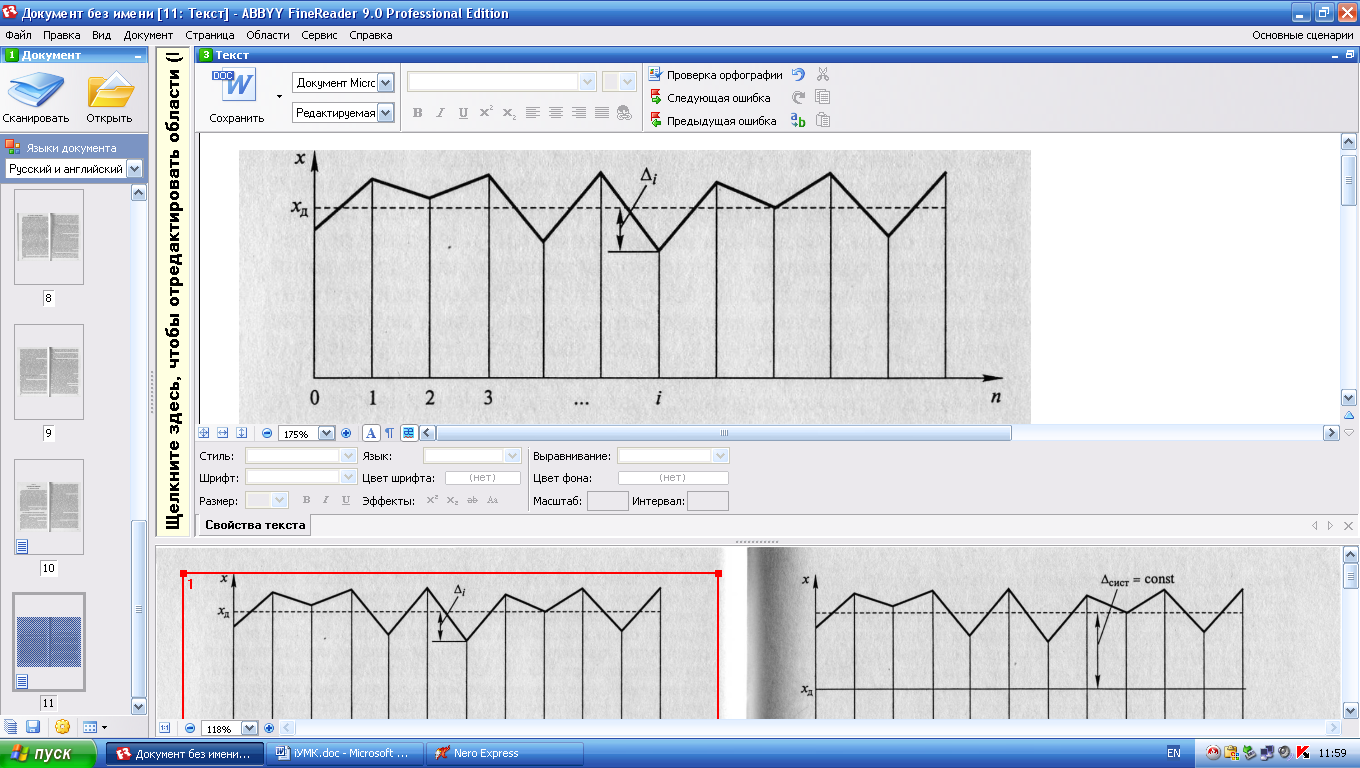
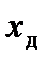 — действительное значение измеряемой величины;
— действительное значение измеряемой величины; 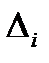 ,- — погрешность i-го измерения; п — число измерений
,- — погрешность i-го измерения; п — число измерений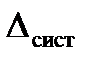 = х - Q). Однако приведенные иллюстрации несколько упрощены, так как систематическая погрешность также содержит некоторый элемент случайности и в некоторой степени обладает свойствами случайной величины. На этом основании предложено считать систематическую погрешность специфической, «выраженной» случайной величиной. Она может также изменяться при многократных измерениях, когда фактор времени или нестабильность измерительной системы вносят заметное изменение в систему.
= х - Q). Однако приведенные иллюстрации несколько упрощены, так как систематическая погрешность также содержит некоторый элемент случайности и в некоторой степени обладает свойствами случайной величины. На этом основании предложено считать систематическую погрешность специфической, «выраженной» случайной величиной. Она может также изменяться при многократных измерениях, когда фактор времени или нестабильность измерительной системы вносят заметное изменение в систему.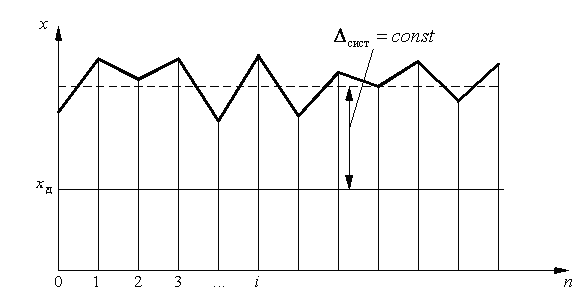

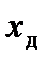 — действительное значение измеряемой величины; п — число измерений;
— действительное значение измеряемой величины; п — число измерений;  — постоянная систематическая погрешность
— постоянная систематическая погрешность


