
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение линейных размеров и объема тела правильной геометрической формыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Л.И. Третьяков
В учебно-методическом пособии приведены описания четырех лабораторных работ по определению линейных размеров тел с помощью штангенциркуля и микрометра, массы тел с помощью технических и аналитических весов, определению плотности твердых тел правильной геометрической формы, жидкостей и сыпучих тел. В каждой работе имеется подробное теоретическое введение, порядок выполнения работы, контрольные вопросы для допуска и защиты, приложения, расширяющие кругозор студентов. Пособие предназначено для студентов естественнонаучных направлений и специальности «Фармация», изучающих курс физики. УДК 531.714:531.753:531.754(075.8) ББК 22.3с+30.10я73
© Новгородский государственный университет, 2008 © Т.П. Смирнова, составление, 2008 ЛАБОРАТОРНАЯ РАБОТА1 ОПРЕДЕЛЕНИЕ ЛИНЕЙНЫХ РАЗМЕРОВ И ОБЪЕМА ТЕЛА ПРАВИЛЬНОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ ЦЕЛИ РАБОТЫ 1. Изучение правил измерения линейных размеров тел с помощью масштабной линейки и методов увеличения точности этих измерений. 2. Изучение устройства и правил использования штангенциркуля и микрометра. 3. Измерение линейных размеров тела правильной геометрической формы, определение погрешностей прямых измерений. 4. Расчет объема тела, определение погрешностей косвенных измерений.
ОСНОВНЫЕ ПОНЯТИЯ В качестве тела правильной геометрической формы в работе рекомендуется использовать прямой прямоугольный параллелепипед либо прямой круговой цилиндр. Объем параллелепипеда равен:
где а – длина; b – ширина; с – высота. Объем цилиндра равен:
где D – диаметр; h – высота цилиндра. Для определения объема необходимо измерить линейные размеры этих тел с помощью масштабной линейки, нониуса и микрометрического винта.
Масштабная линейка Линейка – это инструмент для проведения (черчения) прямых линий*. Линейка, имеющая только один прямолинейный край, называется односторонней. Линейка, имеющая параллельные края, называется двухсторонней. Двухстороння линейка позволяет проводить параллельные прямые линии. Стальная линейка с нанесенными на ней равноудаленными прямыми штрихами является измерительным инструментом или масштабной линейкой (рис. 1.1).
Рис. 1.1. Масштабные линейки
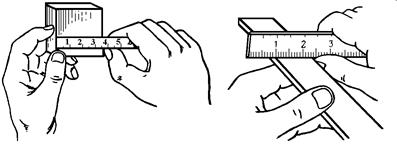
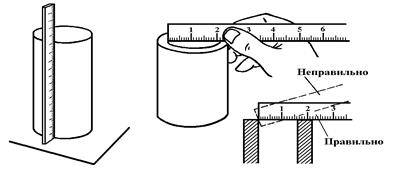
Деление линейки или масштаб* – это расстояние между серединами двух соседних штрихов. Штрихи наносятся на расстоянии 1 мм один от другого (1 мм = 0,001 м = 10-3 м**). Линейка с миллиметровыми делениями – это многозначная мера длины для воспроизведения отрезков, отличающихся на один миллиметр. Нумерация штрихов линейки начинается с нуля. Каждые 5 мм отделяются удлиненным штрихом без обозначений. Каждые 10 мм отделяются длинным штрихом, у которого ставится число, показывающее количество сантиметров, отсчитанных от нулевого штриха. Совокупность штрихов и проставленных у некоторых из них чисел отсчета, соответствующих ряду последовательных значений длины (или другой физической величины), называется шкалой. Началом шкалы измерительных линеек является торцевая грань, перпендикулярная оси линейки. Концом шкалы служит противоположная ей торцевая грань (рис. 1.1, а) или штрих, за которым имеется свободное поле (рис. 1.1, б). Линейкой измеряют контактным способом. Для этого измеряемую деталь необходимо расположить вдоль линейки так, чтобы один ее конец совпал с нулевым штрихом линейки, а затем отсчитать штрих, с которым совпадает другой конец детали. Если второй конец измеряемой детали находится между двумя соседними штрихами, то отсчет делают по ближайшему штриху. Абсолютная погрешность отсчета в этом случае равна половине деления линейки, т.е. 0,5 мм. В этом случае говорят, что измерения проведены с точностью до 0,5 мм. Некоторые приемы измерения масштабной линейкой приведены на рис. 1.2. Линейку следует прикладывать ребром (под прямым углом), а не плоскостью; в случае незначительных повреждений торца линейки следует с краем детали совмещать не нулевой штрих, а, например, десятый, и из полученного результата вычитать 10 мм.
а б
в г Рис. 1.2. Некоторые приемы измерения масштабной линейкой: а, б - ширины детали; в - длины цилиндра; г - внутреннего диаметра цилиндра
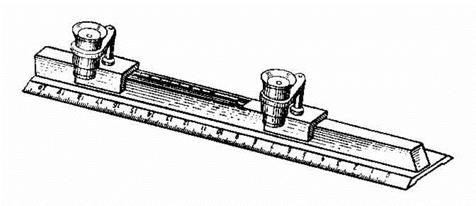
На рис. 1.3 показан образцовый штриховой метр. Деления нанесены на длине 1 м: с одной стороны через 1 мм, а с другой стороны - через 0,2 мм. Для повышения точности отсчета по шкалам имеются две лупы 7-кратного увеличения. Лупы установлены в движках, которые перемещаются по реборде. В реборде вмонтирован термометр, так как наиболее точные показания метра будут при 20°С. Образцовый штриховой метр применяется для проверки шкальных инструментов.
Рис. 1.3. Образцовый штриховой метр
К экономическим показателям выбираемых средств и методов измерения относятся: стоимость измерительного инструмента, продолжительность его работы до ремонта, время, затрачиваемое на процесс измерения. В промышленном производстве для измерения длины тела с точностью до долей миллиметра широко используются инструменты со вспомогательной шкалой (нониусом) либо микрометрическим винтом. Нониус Измерения с помощью нониуса Сравнивать длину детали с отрезками многозначной меры, концы которых нужно искать на двух неподвижно закрепленных как указано выше линейках, неудобно. Поступим иначе. Начнем медленно сдвигать вправо линейку нониуса с меньшими делениями. Нулевые штрихи разойдутся. Затем совпадут первые штрихи линеек. Это произойдет при сдвиге нулевых штрихов на величину ∆l, равную точности нониуса D N -ые штрихи, т.е. в этом случае т = N (см. рис. 1.4). Аналогичные наблюдения можно сделать при смещении нулевого штриха верхней линейки относительно первого штриха нижней линейки, затем относительно второго, третьего и т.д. В любом положении линеек нониуса один из штрихов верхней линейки (из первых N) совпадает с каким-либо штрихом нижней линейки или очень близко расположен к нему. Отсчет по нониусу основан на способности глаза фиксировать это совпадение. На практике линейку с малыми делениями делают обычно короткой, чтобы со штрихами второй линейки совпадал только один штрих этой линейки. Длинную линейку называют основной шкалой или масштабом, короткую – дополнительной шкалой, нониусом или верньером (по имени изобретателя – французского математика П. Вернье (1580-1637)). Рассмотрим процесс измерений с помощью нониуса. Пусть L – длина измеряемого образца (рис. 1.5). Совместим с началом образца нулевой штрих масштаба. Пусть при этом конец образца окажется между k -м и (k + 1)-м штрихами масштаба. Тогда в длине образца содержится k целых делений масштаба и отрезок
Рис. 1.5. Измерение длины детали с помощью нониуса
Для определения отрезка
Тогда вся длина будет равна
Результат можно сформулировать следующим образом: длина образца, измеряемая с помощью нониуса, равна длине целых делений масштаба до нулевого штриха нониуса плюс отрезок, равный произведению точности нониуса на номер штриха нониуса, совпадающего с некоторым штрихом масштаба. Погрешность, которая может возникнуть при таком методе отсчета, обусловлена неточным совпадением т -го штриха нониуса с (k + т)-м штрихом масштаба. Значение ее не будет превышать, очевидно, величину На рис. 1.6 изображен в увеличенном виде измерительный инструмент, у которого наименьшее деление масштаба у =
Рис. 1.6. Примеры измерений с помощью нониуса: а - L = 0,6 мм; б - L = 7,0 мм; в - L = 7,4 мм
Расширенный нониус Нониус не на всех приборах одинаков. Обычно в теории рассматривается случай, когда каждое деление нониуса на величину
где
На рис. 1.7 изображены в увеличенном виде основная шкала и расширенный нониус: наименьшее деление основной шкалы у = 1 мм; наименьшее деление нониуса х = 1,9 мм; отрезок основной шкалы, соизмеримый с наименьшим делением нониуса,
Рис. 1.7. Расширенный нониус
Точность расширенного нониуса можно найти из уравнения нониуса. Пусть N – число делений на нониусе, тогда длина линейки нониуса (всех его N делений) равна Nх. Длина линейки нониуса меньше длины такого же числа N отрезков масштаба
Выразив отсюда х и подставив в формулу (1.12), получим точность расширенного нониуса
- как N -ую долю наименьшего деления масштаба (ср. с формулой (1.7)). Модуль нониуса равен
Правила отсчета длины тела с помощью расширенного нониуса такие же, как и при использовании простейшего нониуса. Различные типы нониусов приведены в приложении 1.6.2. Нониусы используются в штангенциркулях, теодолитах, сахариметрах, препаратоводителях микроскопов и многих других приборах. Штангенциркуль
Штангенциркуль служит для измерений контактным способом линейных размеров тел, при которых не требуется высокая точность, т.е. с абсолютной погрешностью от 0,02 мм до 0,1 мм. Штангенциркуль предназначен для наружных и внутренних измерений, а также для измерения глубины или высоты выступа. Основной частью штангенциркуля (рис. 1.8) является масштабная линейка 1 или штанга, на которой нанесена миллиметровая шкала. Продольные грани штанги параллельны между собой. Вдоль штанги скользит подвижная рамка 6 с нониусом 8. Точность нониуса обычно указана на штанге. Положение рамки на штанге может быть зафиксировано с помощью винта 7.
Рис. 1.8. Штангенциркуль ШЦ–I: 1– штанга; 2 – подвижная нижняя ножка; 3 – неподвижная нижняя ножка; 4 – неподвижная верхняя ножка; 5 – подвижная верхняя ножка; 6 – рамка; 7 – винт для зажима рамки; 8 – нониус; 9 – линейка глубиномера
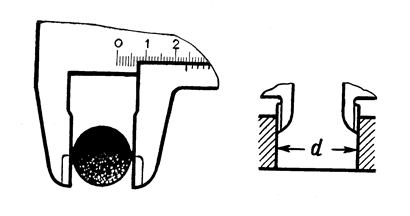
Неподвижная ножка (губка) 3 жестко скреплена (или составляет одно целое) со штангой и является упором. Измерительная поверхность ножки строго перпендикулярна продольным граням штанги. Подвижная рамка и подвижная ножка 2 также представляют одно целое. Рамка обеспечивает плавное передвижение подвижной ножки и ее устойчивое положение относительно штанги. Внутренние грани рамки плотно прилегают к наружным граням штанги – это обеспечивает параллельность измерительных поверхностей ножек, что очень важно при измерениях. Когда измерительные поверхности ножек соприкасаются, нулевой штрих нониуса совпадает с нулевым штрихом масштаба. Если измерительные поверхности не соприкасаются, то расстояние между ними равно расстоянию между нулевыми штрихами масштаба и нониуса. Штангенциркуль типа ШЦ-I с пределами измерений 0 – 125 мм (рис. 1.8) имеет две пары измерительных ножек. Две нижние ножки (2 и 3) служат для наружных измерений (рис. 1.9, а), а две верхние ножки (4 и 5) – для внутренних (рис. 1.9, б). Верхние ножки расположены так, что при измерении внутренних размеров отсчет ведется от нуля, т.е. так же, как и при измерении наружных размеров.
а б
Рис. 1.9. Измерение с помощью штангенциркуля Рис. 1.10. Измерение ШЦ-I: а – наружных размеров; б – внутренних размеров глубины отверстия
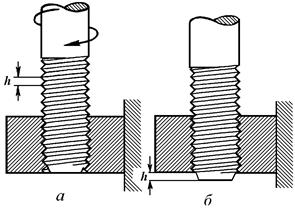
Штангенциркуль ШЦ-I снабжен глубиномером в виде линейки или стержня 9 (рис. 1.8), который жестко скреплен с подвижной рамкой. Если измерительные поверхности ножек соприкасаются (нулевые штрихи совпадают), то торец глубиномера совпадает с торцом штанги. При перемещении рамки линейка глубиномера выдвигается. На сколько нулевой штрих нониуса сдвинут относительно нулевого штриха масштаба, на столько же линейка глубиномера выступает за торец штанги. Линейка глубиномера применяется для измерения глубины или высоты выступа (рис. 1.10). Существует несколько видов штангенциркулей. Они отличаются типом и количеством измерительных ножек, длиной штанги, типом нониуса и наличием некоторых вспомогательных деталей (см. приложение 1.6.3). Микрометрический винт 1.2.3.1. Микрометрический винт – многозначная мера длины Принцип работы микрометрических инструментов основан на использовании относительного перемещения деталей винтовой пары (гайка – винт). В одних случаях винт вращается по внутренней резьбе неподвижной гайки, в других – гайка вращается по внешней резьбе неподвижного винта. Шаг микрометрического винта или шаг резьбы h равен расстоянию между соседними нарезками винта (рис. 1.12, а) и очень точно выдержан вдоль всей его длины.
Рис. 1.12. Винтовая пара гайка-винт с шагом резьбы h
В винтовой паре вращательное движение одного из ее элементов (винта или гайки) связано одновременно с его перемещением вдоль оси относительно неподвижного другого элемента. Величина перемещения вдоль оси будет тем больше, чем больше величина угла поворота. При одном полном обороте винта в неподвижной гайке продольное перемещение винта вдоль оси равно шагу резьбы h (рис. 1.12, б). При двух полных оборотах винта продольное перемещение равно 2 h, при трех оборотах – и 3 h т.д. Если на головку винта нанести N = 100 равноудаленных штрихов, то при повороте винта на 1 деление (0,01 оборота) винт сместится вдоль оси на 0,01 шага винта, при повороте на 2 деления смещение вдоль оси составит 0,02 шага винта и т.д. Таким образом, винтовая пара – многозначная мера длины для воспроизведения отрезков, отличающихся на Микрометрический винт применяется в более точных измерительных приборах – микрометрах, микроскопах и других.
Микрометр Основной деталью микрометра является подвижный микрометрический винт. Микрометр служит для измерений контактным способом линейных размеров тел с точностью до 0,01 мм (у некоторых микрометров – до 0,001 мм)*. Микрометр (рис. 1.13) состоит из массивной скобы 1, в муфтах 2 и 5 которой находятся с одной стороны стержень 4 микрометрического винта, с другой – опорная пята 3. Отполированные поверхности торцов опорной пяты и стержня микрометрического винта являются измерительными поверхностями. На другом конце стержня нанесена внешняя микрометрическая резьба. Этот конец находится внутри неподвижной полой трубки (стебля) 6, имеющей внутреннюю резьбу, и прочно соединен с подвижной полой трубкой 7, которую называют барабаном. С помощью барабана происходит перемещение микрометрического винта. Предел измерения микрометрическим инструментом ограничивается 25 мм. Это вызвано технологическими причинами – необходимостью обеспечивать требуемую точность при нарезании микрометрической резьбы.
Рис. 1.13. Микрометр: 1 – скоба; 2 – левая муфта; 3 опорная пята; 4 – стержень микрометрического винта; 5 – правая муфта; 6 – неподвижная полая трубка (стебель); 7 – подвижная полая трубка (барабан); 8 – головка трещотки На неподвижной трубке нанесены продольная линия и основная (неподвижная) шкала. Расстояние между ближайшими штрихами этой шкалы равно шагу микрометрического винта. Если на неподвижной трубке нанесены только миллиметровые деления, то шаг винта равен 1 мм; если же обозначены еще и половинки миллиметров, то шаг винта равен 0,5 мм. Продольная линия служит нулевой линией для отсчета долей миллиметра по барабану. Наиболее распространенным является микрометр, у которого шаг микрометрического винта равен 0,5 мм. Цена деления неподвижной шкалы стебля 0,5 мм. Штрихи нанесены как под нулевой продольной линией, так и над ней. Шаг винта равен расстоянию между ближайшими верхним и нижним штрихами. Цифры проставлены только у нижних штрихов, т.е. нижняя шкала представляет собой обычную миллиметровую линейку. Верхние штрихи сдвинуты относительно нижних на 0,5 мм и при отсчете соответствуют половинкам миллиметра. На барабане наискось срезан один конец. На этом срезе нанесена шкала, которая является подвижной. На шкале барабана нанесено 50 равных делений. Поворот барабана на одно деление соответствует перемещению микрометрического винта и его стержня вдоль оси на 1/50 шага винта, что составляет 0,01 мм. Это сделано для удобства отсчета. При работе с микрометром нужно помнить, что главным источником ошибок является неконтролируемость нажатия микрометрического винта на измеряемый предмет. Дело в том, что винт с малым шагом превращает незначительные усилия руки, поворачивающей винт, в большие силы, действующие на измеряемый предмет и на микрометрическую резьбу. Это может привести как к деформации предмета, так и к преждевременному износу и повреждению микрометрической резьбы. Для устранения этого недостатка рукоятка микрометра снабжена специальной головкой 8 – «трещоткой». Трещотка имеет холостой ход, т.е. продолжает вращаться, когда винт и барабан уже неподвижны. Это позволяет создать небольшие и всякий раз одинаковые, заданные ГОСТом, мерительные силы давления на измеряемый объект. Конструкция трещотки приведена на рис. 1.14 (1 – храповик; 2 – сухарь; 3 – пружина). Принцип работы трещотки состоит в следующем. Зубец храповика при вращении головки 8 (рис. 1.12) выходит из зацепления, как только момент силы трения между измерительной поверхностью стержня микрометрического винта и измеряемой деталью будет превышать момент силы сцепления храповика и сухарика. Величина этой силы зависит от жестокости пружины и угла α наклона зубцов храповика. Измерительное усилие не должно превышать 5-9 ньютонов. Такое усилие вполне достаточно для полноты и устойчивости контакта детали с измерительными поверхностями микрометра.
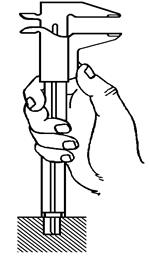
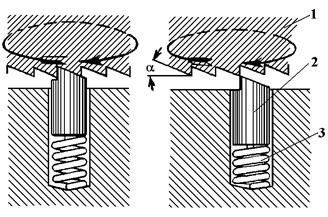
Рис. 1.14. Устройство и схема работы трещотки микрометра: 1 – храповик; 2 – сухарь; 3 – пружина Подготовка микрометра к измерениям Перед измерением необходимо определить начальное показание инструмента. Для этого нужно привести в соприкосновение измерительные поверхности стержня микрометрического винта и опорной пяты (рис. 1.15). Кромка среза барабана при этом должна совпадать с нулевым штрихом неподвижной шкалы стебля, вся неподвижная шкала должна быть закрыта, а нулевой штрих барабана должен совпадать с нулевой линией. Если такого совпадения нет, то нужно либо учесть систематическую погрешность, введя поправку к отсчету, либо устранить этот недостаток.
Рис. 1.15. Проверка начального показания микрометра Приборы и оборудование
Микрометр, штангенциркуль, тело правильной геометрической формы (параллелепипед или цилиндр). Порядок выполнения работы ЗАДАНИЕ1 Подготовка штангенциркуля к работе 1. Перед измерениями необходимо внимательно осмотреть штангенциркуль – нет ли перекосов ножек, нет ли зазора между штангой и подвижной рамкой. Нельзя пользоваться неисправным инструментом. Штангенциркули с перекошенными ножками, имеющие «игру» рамки, стертые штрихи и т.д., для измерений не годятся. 2. Привести в соприкосновение измерительные поверхности ножек штангенциркуля и определить точность нониуса. Если при соприкосновении измерительных поверхностей нулевой штрих нониуса не совпадает с нулевым штрихом масштаба, то нужно определить систематическую погрешность инструмента. При измерениях ее необходимо учитывать, вводя поправку к отсчету. Записать в табл. 1.1 точность нониуса, систематическую погрешность штангенциркуля и другие данные.
Таблица 1.1
Примечание. Поправкой называют значение величины, одноименное с измеряемой, которое необходимо прибавить к полученному при измерении значению, чтобы исключить систематическую погрешность.
ЗАДАНИЕ 3
Подготовка микрометра к работе 1. Медленно вращая барабан за головку трещотки, ознакомиться с тем, как открываются штрихи на верхней и нижней частях неподвижной шкалы. Определить шаг микрометрического винта и цену деления подвижной шкалы барабана. 2. Привести в соприкосновение торец стержня микрометрического винта с опорной пятой, определить систематическую погрешность микрометра, записать эти и другие данные в табл. 1.2.
Таблица 1.2
ЗАДАНИЕ 5
ТЕХНИКА БЕЗОПАСНОСТИ На рабочем месте могут находиться только необходимые в данной работе приборы и оборудование.
КОНТРОЛЬНЫЕ ВОПРОСЫ
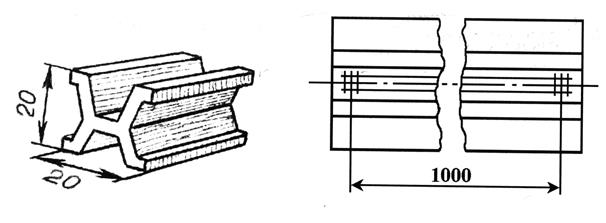
1. Что такое масштабная линейка? Каковы ее достоинства и недостатки? 2. Какие методы позволяют увеличить точность измерения линейных размеров тел? 3. Что такое нониус, каково его назначение? 4. Каково устройство штангенциркуля? 5. Как найти длину тела с помощью штангенциркуля? 6. Каково устройство микрометра? 7. Как найти длину тела с помощью микрометра? 8. Назовите правила использования и хранения штангенциркуля и микрометра? 9. Что такое уравнение нониуса? Точность нониуса? Какой нониус называют расширенным? Каковы его преимущества? Как определить точность нониуса штангенциркуля? 10. Покажите, как измерить внутренний размер детали и высоту выступа. 11. Какой винт называют микрометрическим? 12. Какое расстояние называют шагом или ходом винта? 13. На какое расстояние смещается микрометрический винт вдоль оси при повороте барабана на одно деление? 14. Каково назначение трещотки? Каков принцип работы трещотки? 15. Что такое прямые измерения? 16. Как рассчитать абсолютную погрешность прямого измерения? Что такое средняя абсолютная погрешность? Как ее найти? 17. Что такое относительная погрешность? Как рассчитать относительную погрешность прямого измерения? 18. Какая из погрешностей – инструментальная или погрешность отсчета – оказалась преобладающей при измерении линейных размеров тела? 19. В каких случаях следует пользоваться штангенциркулем, в каких – микрометром? 20. Можно ли уменьшить ошибку измерений, применяя микроскоп для наблюдения штрихов линейки? 21. С какой целью деления на чертежных линейках наносят на наклонных краях? Какая из погрешностей при этом уменьшается? 22. Какие измерения называют косвенными? Как определить искомую величину при косвенных измерениях? 23. Как рассчитать абсолютную и относительную погрешности при косвенных измерениях? 24. Какая из измеренных величин вносит максимальный вклад в относительную погрешность объема? 25. Предложите способы уменьшения погрешности измерений объема тела. Вопросы для допуска: 1–8. Вопросы для защиты: 9–25. ПРИЛОЖЕНИЕ 1.6.1. Единица длины – метр «Метр – длина, равная 1 650 763,73 длин волн в вакууме излучения, соответствующего переходу между уровнями 2р10 и 5d5 атома криптона 86» (ГОСТ 9867-61). Впервые метр был определен как одна десятимиллионная часть четверти Парижского меридиана. При установлении Метрической системы мер измерения части дуги этого меридиана были произведены комиссией ученых, созданной Парижской Академией наук. На основе этих измерений был изготовлен прототип метра, утвержденный Национальным собранием Франции в 1799 г. Прототип метра представлял собой платиновую линейку шириной около 25 мм, толщиной около 4 мм с расстоянием между концами, равным одному метру. Этот прототип получил название «метр Архива» и хранится в Национальном архиве Франции. Позднее выяснилось, что при повторных измерениях метр не может быть точно воспроизведен в силу неизбежных ошибок, допускаемых при измерениях, а также потому, что отсутствовали точные данные о фигуре Земли. Поэтому пришлось отказаться от этого «естественного» эталона метра и принять в качестве исходной меры длины «метр Архива». По нему был изготовлен 31 эталон из платиноиридиевого сплава. Сплав платины и иридия был выбран как обладающий очень малым коэффициентом расширения. Один из эталонов (эталон № 6), как наиболее точно воспроизводивший «метр Архива», по постановлению I Генеральной конференции по мерам и весам в 1889 г. был утвержден в качестве Международного прототипа метра. Международный эталон метра представлял собой стержень Х-образного сечения длиной 102 см (рис. 1.19, размеры указаны в миллиметрах: а) вид сбоку; б) вид сверху). Форма поперечного сечения эталона отвечала требованию возможно меньшего прогиба. На обоих концах эталона на специально отполированных участках нанесены по три поперечных и два продольных штриха. Расстояние между осями средних поперечных штрихов при температуре тающего льда было принято за 1 метр.
а б Рис. 1.19. Международный прототип метра, утвержденный I Генеральной конференцией по мерам и весам в 1889 г.: а - вид сбоку; б - вид сверху
Для государств, перешедших на метрическую систему, были изготовлены копии прототипа метра, которые были распределены по жеребьевке. России достались метры № 28 (государственный эталон) и № 11 (эталон-свидетель для контроля государственного эталона). Однако, определение метра с помощью штрихового эталона неудовлетворительно в двух отношениях. Во-первых, штриховой прототип метра является искусственным и, в случае утраты, не может быть воспроизведен. Во-вторых, это определение не обеспечивало необходимой точности. Ширина штрихов, нанесенных на прототипе метра и устанавливающих его длину, составляла 10 мкм. Поэтому при сличении государственных эталонов метра с прототипом неизбежно допускалась абсолютная погрешность не менее 0,1 мкм или относительная погрешность 10-7. Такая точность является недостаточной как для научных целей, так и для ряда отраслей промышленного производства. Поэтому в 1960 году XI Генеральная конференция по мерам и весам постановила определить метр как длину, равную некоторому числу длин световых волн. Известно, что раскаленные пары и газы дают линейчатые спектры излучения. Каждая линия спектра данного газа соответствует переходу электрона в атоме с одного стационарного состояния с бо́льшим значением энергии Е1 в другое стационарное состояние с меньшим значением энергии Е2 (Е1 > Е2). При этом излучается квант света, частота
где h – постоянная Планка. Тогда длина волны
где с – скорость света в вакууме. Длины волн спектральных линий подчиняются строгим закономерностям. Поэтому длина волны, соответствующая какой-либо спектральной линии, или некоторое число этих длин волн, может быть принято за естественный эталон длины. Но спектральные линии в линейчатых спектрах не являются строго монохроматическими. Каждая линия содержит не одну длину волны Ширина спектральной линии может в той или иной степени меняться в зависимости от условий излучения. Эта зависимость для разных линий различна. Поэтому за основу эталона длины необходимо брать длину волны, соответствующую такой линии, ширина которой более стабильна. Таким образом, за основу эталона длины следует выбрать излучение такого химического элемента, в спектре которого имеется наиболее узкая линия, отличающаяся в то же время максимально возможным постоянством ширины. В результате многочисленных исследований было найдено, что наилучшим образом этим двум требованиям удовлетворяет оранжевая линия в спектре криптона. Поскольку естественный криптон содержит шесть стабильных изотопов, спектральные линии которых хотя и в малой степени, но отличаются друг от друга, то определение метра через длину волны уточняется указанием на то, что в качестве источника берется излучение наиболее тяжелого изотопа криптона с массовым числом 86 (36Kr86). Принятая спектральная линия соответствует переходу электрона в атоме криптона между квантовыми состояниями, которые в спектроскопии обозначаются символами 2р10 и 5d5. По определению, которое было указано в начале этого параграфа, метр содержит 1 650 763,73 длины волны в вакууме этой спектральной линии. Схема устройства лампы, наполненной изотопом криптона 86 и используемой для воспроизведения единицы длины метра в длинах световых волн, приведена на рис. 1.20. Газоразрядная лампа представляет собой U-образную трубку 2 со средней частью в виде капилляра 1 длиной 10 – 12 см и внутренним диаметром 2 - 4 мм. Лампа имеет накаливаемый катод 3 и анод 5. Газоразрядная криптоновая лампа помещается в сосуд Дьюара 6 с жидким азотом. Дьюаровский сосуд находится в герметически закрытой камере 7. Откачивая испаряющийся азот насосом, понижают температуру внутри сосуда и обеспечивают в камере условия, соответствующие тройной точке азота (
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1065; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.013 с.) |

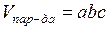 , (1.1)
, (1.1)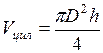 , (1.2)
, (1.2)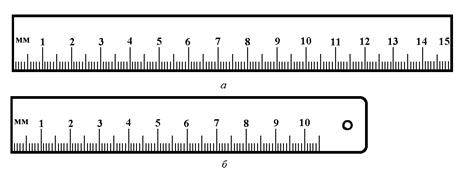
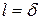 . Вторые штрихи линеек совпадут при сдвиге нулевых штрихов на две точности нониуса D
. Вторые штрихи линеек совпадут при сдвиге нулевых штрихов на две точности нониуса D 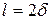 и т.д. Если совпали
и т.д. Если совпали 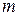 -е штрихи, то можно утверждать, что нулевые штрихи сдвинуты на D
-е штрихи, то можно утверждать, что нулевые штрихи сдвинуты на D 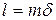 . При сдвиге ровно на одно большое деление
. При сдвиге ровно на одно большое деление 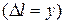 нулевой штрих верхней линейки совпадает с первым штрихом нижней линейки и совпадают
нулевой штрих верхней линейки совпадает с первым штрихом нижней линейки и совпадают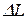 – неизвестная пока еще доля (k +1)-го деления масштаба:
– неизвестная пока еще доля (k +1)-го деления масштаба: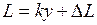 . (1.8)
. (1.8)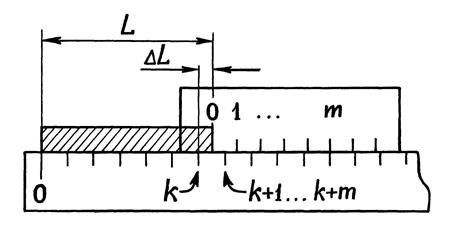
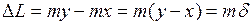 . (1.9)
. (1.9)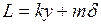 . (1.10)
. (1.10)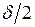 , ибо при большем несовпадении этих штрихов, один из соседних штрихов нониуса (справа или слева) имел бы несовпадение меньше
, ибо при большем несовпадении этих штрихов, один из соседних штрихов нониуса (справа или слева) имел бы несовпадение меньше 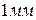 , наименьшее деление нониуса
, наименьшее деление нониуса 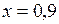 мм, точность нониуса
мм, точность нониуса 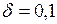 мм, N = 10. Из рисунка видно, что расстояние между нулевыми штрихами масштаба и нониуса в случае «а» равно 0,6 мм, в случае «б» – 7,0 мм, в случае «в» – 7,4 мм.
мм, N = 10. Из рисунка видно, что расстояние между нулевыми штрихами масштаба и нониуса в случае «а» равно 0,6 мм, в случае «б» – 7,0 мм, в случае «в» – 7,4 мм.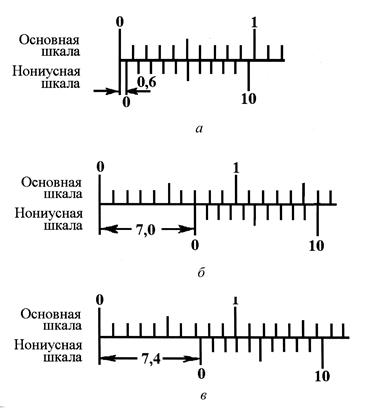
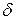 меньше одного наименьшего деления масштаба. Однако на практике для удобства измерений нониус «растягивают» так, чтобы каждое его деление было на величину
меньше одного наименьшего деления масштаба. Однако на практике для удобства измерений нониус «растягивают» так, чтобы каждое его деление было на величину 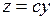 , (1.11)
, (1.11)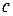 – целое число, которое называется модулем нониуса. Такой нониус называют расширенным или растянутым. Точность расширенного нониуса равна разности отрезка
– целое число, которое называется модулем нониуса. Такой нониус называют расширенным или растянутым. Точность расширенного нониуса равна разности отрезка 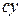 масштаба и наименьшего деления нониуса
масштаба и наименьшего деления нониуса 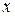
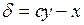 . (1.12)
. (1.12)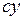 = 2 мм, модуль нониуса с = 2; число делений на нониусе N = 10; точность нониуса
= 2 мм, модуль нониуса с = 2; число делений на нониусе N = 10; точность нониуса 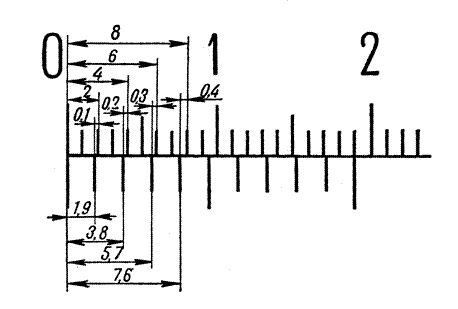
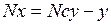 . (1.13)
. (1.13)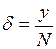 (1.14)
(1.14)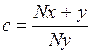 . (1.15)
. (1.15)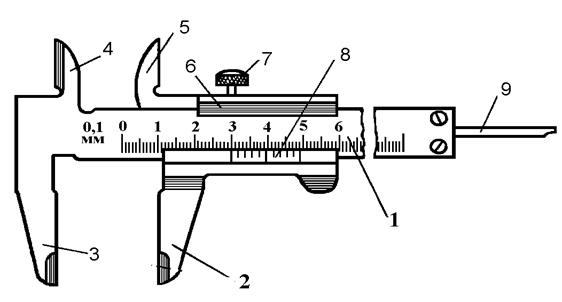
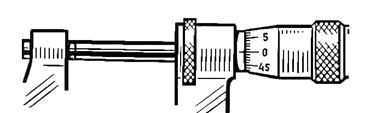
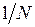 долю шага микрометрического винта, где N – число делений на головке винта.
долю шага микрометрического винта, где N – число делений на головке винта.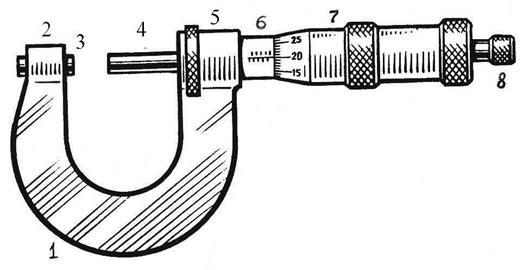
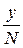
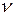 которого определяется из условия
которого определяется из условия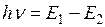 , (1.34)
, (1.34)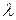 равна
равна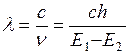 , (1.35)
, (1.35)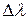 вблизи длины волны
вблизи длины волны 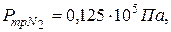
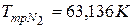 ). При температуре тройной точки азота газоразрядная лампа содержит твердую фазу криптона 86 (
). При температуре тройной точки азота газоразрядная лампа содержит твердую фазу криптона 86 (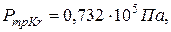
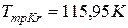 ). Температура капилляра измеряется термопарой 8, а давление паров азота – манометром 4. Плотность разрядно
). Температура капилляра измеряется термопарой 8, а давление паров азота – манометром 4. Плотность разрядно 


