Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение устройства микрометраСодержание книги
Поиск на нашем сайте
1. Изучить устройство микрометра.
ЗАДАНИЕ 4
Подготовка микрометра к работе 1. Медленно вращая барабан за головку трещотки, ознакомиться с тем, как открываются штрихи на верхней и нижней частях неподвижной шкалы. Определить шаг микрометрического винта и цену деления подвижной шкалы барабана. 2. Привести в соприкосновение торец стержня микрометрического винта с опорной пятой, определить систематическую погрешность микрометра, записать эти и другие данные в табл. 1.2.
Таблица 1.2
ЗАДАНИЕ 5
Измерение линейных размеров тела правильной геометрической формы и расчет погрешностей при прямых измерениях 1. Измерить длину а параллелепипеда 5 раз. Результаты измерений записать в табл. 1.3.
Таблица 1.3
Измерительный инструмент: Инструментальная погрешность:
Вычислить среднее значение длины
Рассчитать абсолютную погрешность каждого отсчета*:
Рассчитать среднюю абсолютную погрешность отсчета:
Записать, каким измерительным прибором проводились измерения длины тела и его инструментальную погрешность
Записать результат в форме:
2. Измерить ширину b и высоту с параллелепипеда. Результаты измерений занести в таблицы аналогичные табл. 1.3. Результаты представить в форме:
[*]
Примечание. Правила округления 1. Если старшая отбрасываемая цифра меньше 5, то последняя сохраняемая цифра не изменяется. 2. Если старшая отбрасываемая цифра больше или равна 5, то последняя сохраняемая цифра увеличивается на единицу. 3. Если при округлении последняя сохраняемая цифра оказалась нулем, то его следует писать, даже если он стоит в разряде десятичных дробей.
4. Из правил округления имеется существенное исключение – при округлении погрешностей последняя сохраняемая цифра увеличивается на единицу, если старшая отбрасываемая цифра 3 или больше 3. 5. Физическая величина округляется до первой сомнительной цифры. Все цифры, стоящие после сомнительной, отбрасываются. 6. Абсолютная погрешность округляется до одной значащей цифры, относительная – до двух значащих цифр. 7. При вычислении промежуточных результатов следует брать на одну цифру больше. В окончательном результате эта «запасная» цифра отбрасывается.
ЗАДАНИЕ 6
Определение объема прямого прямоугольного параллелепипеда И расчет погрешностей при косвенных измерениях Рассчитать объем прямого прямоугольного параллелепипеда по формуле:
Рассчитать относительную погрешность объема:
Сравнить вклад, который вносят погрешности величин a, b, c в относительную погрешность объема. Сделать вывод. Вычислить абсолютную погрешность объема:
Записать результат в форме:
Сделать выводы по проведенному эксперименту. ЗАДАНИЕ 7
Определение объема прямого кругового цилиндра И расчет погрешностей при косвенных измерениях Измерить диаметр D и высоту h прямого кругового цилиндра. Рассчитать объем прямого кругового цилиндра по формуле:
Относительная погрешность объема цилиндра равна:
Оценить вклад, который вносят погрешности величин D и h в относительную погрешность объема. Сделать вывод. Вычислить абсолютную погрешность объема:
Записать результат в форме V = Сделать выводы по проведенному эксперименту.
ТЕХНИКА БЕЗОПАСНОСТИ На рабочем месте могут находиться только необходимые в данной работе приборы и оборудование.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое масштабная линейка? Каковы ее достоинства и недостатки? 2. Какие методы позволяют увеличить точность измерения линейных размеров тел? 3. Что такое нониус, каково его назначение? 4. Каково устройство штангенциркуля? 5. Как найти длину тела с помощью штангенциркуля? 6. Каково устройство микрометра? 7. Как найти длину тела с помощью микрометра?
8. Назовите правила использования и хранения штангенциркуля и микрометра? 9. Что такое уравнение нониуса? Точность нониуса? Какой нониус называют расширенным? Каковы его преимущества? Как определить точность нониуса штангенциркуля? 10. Покажите, как измерить внутренний размер детали и высоту выступа. 11. Какой винт называют микрометрическим? 12. Какое расстояние называют шагом или ходом винта? 13. На какое расстояние смещается микрометрический винт вдоль оси при повороте барабана на одно деление? 14. Каково назначение трещотки? Каков принцип работы трещотки? 15. Что такое прямые измерения? 16. Как рассчитать абсолютную погрешность прямого измерения? Что такое средняя абсолютная погрешность? Как ее найти? 17. Что такое относительная погрешность? Как рассчитать относительную погрешность прямого измерения? 18. Какая из погрешностей – инструментальная или погрешность отсчета – оказалась преобладающей при измерении линейных размеров тела? 19. В каких случаях следует пользоваться штангенциркулем, в каких – микрометром? 20. Можно ли уменьшить ошибку измерений, применяя микроскоп для наблюдения штрихов линейки? 21. С какой целью деления на чертежных линейках наносят на наклонных краях? Какая из погрешностей при этом уменьшается? 22. Какие измерения называют косвенными? Как определить искомую величину при косвенных измерениях? 23. Как рассчитать абсолютную и относительную погрешности при косвенных измерениях? 24. Какая из измеренных величин вносит максимальный вклад в относительную погрешность объема? 25. Предложите способы уменьшения погрешности измерений объема тела. Вопросы для допуска: 1–8. Вопросы для защиты: 9–25. ПРИЛОЖЕНИЕ 1.6.1. Единица длины – метр «Метр – длина, равная 1 650 763,73 длин волн в вакууме излучения, соответствующего переходу между уровнями 2р10 и 5d5 атома криптона 86» (ГОСТ 9867-61). Впервые метр был определен как одна десятимиллионная часть четверти Парижского меридиана. При установлении Метрической системы мер измерения части дуги этого меридиана были произведены комиссией ученых, созданной Парижской Академией наук. На основе этих измерений был изготовлен прототип метра, утвержденный Национальным собранием Франции в 1799 г. Прототип метра представлял собой платиновую линейку шириной около 25 мм, толщиной около 4 мм с расстоянием между концами, равным одному метру. Этот прототип получил название «метр Архива» и хранится в Национальном архиве Франции. Позднее выяснилось, что при повторных измерениях метр не может быть точно воспроизведен в силу неизбежных ошибок, допускаемых при измерениях, а также потому, что отсутствовали точные данные о фигуре Земли. Поэтому пришлось отказаться от этого «естественного» эталона метра и принять в качестве исходной меры длины «метр Архива». По нему был изготовлен 31 эталон из платиноиридиевого сплава. Сплав платины и иридия был выбран как обладающий очень малым коэффициентом расширения. Один из эталонов (эталон № 6), как наиболее точно воспроизводивший «метр Архива», по постановлению I Генеральной конференции по мерам и весам в 1889 г. был утвержден в качестве Международного прототипа метра. Международный эталон метра представлял собой стержень Х-образного сечения длиной 102 см (рис. 1.19, размеры указаны в миллиметрах: а) вид сбоку; б) вид сверху). Форма поперечного сечения эталона отвечала требованию возможно меньшего прогиба. На обоих концах эталона на специально отполированных участках нанесены по три поперечных и два продольных штриха. Расстояние между осями средних поперечных штрихов при температуре тающего льда было принято за 1 метр.
а б Рис. 1.19. Международный прототип метра, утвержденный I Генеральной конференцией по мерам и весам в 1889 г.: а - вид сбоку; б - вид сверху
Для государств, перешедших на метрическую систему, были изготовлены копии прототипа метра, которые были распределены по жеребьевке. России достались метры № 28 (государственный эталон) и № 11 (эталон-свидетель для контроля государственного эталона). Однако, определение метра с помощью штрихового эталона неудовлетворительно в двух отношениях. Во-первых, штриховой прототип метра является искусственным и, в случае утраты, не может быть воспроизведен. Во-вторых, это определение не обеспечивало необходимой точности. Ширина штрихов, нанесенных на прототипе метра и устанавливающих его длину, составляла 10 мкм. Поэтому при сличении государственных эталонов метра с прототипом неизбежно допускалась абсолютная погрешность не менее 0,1 мкм или относительная погрешность 10-7. Такая точность является недостаточной как для научных целей, так и для ряда отраслей промышленного производства. Поэтому в 1960 году XI Генеральная конференция по мерам и весам постановила определить метр как длину, равную некоторому числу длин световых волн. Известно, что раскаленные пары и газы дают линейчатые спектры излучения. Каждая линия спектра данного газа соответствует переходу электрона в атоме с одного стационарного состояния с бо́льшим значением энергии Е1 в другое стационарное состояние с меньшим значением энергии Е2 (Е1 > Е2). При этом излучается квант света, частота
где h – постоянная Планка. Тогда длина волны
где с – скорость света в вакууме. Длины волн спектральных линий подчиняются строгим закономерностям. Поэтому длина волны, соответствующая какой-либо спектральной линии, или некоторое число этих длин волн, может быть принято за естественный эталон длины. Но спектральные линии в линейчатых спектрах не являются строго монохроматическими. Каждая линия содержит не одну длину волны
Ширина спектральной линии может в той или иной степени меняться в зависимости от условий излучения. Эта зависимость для разных линий различна. Поэтому за основу эталона длины необходимо брать длину волны, соответствующую такой линии, ширина которой более стабильна. Таким образом, за основу эталона длины следует выбрать излучение такого химического элемента, в спектре которого имеется наиболее узкая линия, отличающаяся в то же время максимально возможным постоянством ширины. В результате многочисленных исследований было найдено, что наилучшим образом этим двум требованиям удовлетворяет оранжевая линия в спектре криптона. Поскольку естественный криптон содержит шесть стабильных изотопов, спектральные линии которых хотя и в малой степени, но отличаются друг от друга, то определение метра через длину волны уточняется указанием на то, что в качестве источника берется излучение наиболее тяжелого изотопа криптона с массовым числом 86 (36Kr86). Принятая спектральная линия соответствует переходу электрона в атоме криптона между квантовыми состояниями, которые в спектроскопии обозначаются символами 2р10 и 5d5. По определению, которое было указано в начале этого параграфа, метр содержит 1 650 763,73 длины волны в вакууме этой спектральной линии. Схема устройства лампы, наполненной изотопом криптона 86 и используемой для воспроизведения единицы длины метра в длинах световых волн, приведена на рис. 1.20. Газоразрядная лампа представляет собой U-образную трубку 2 со средней частью в виде капилляра 1 длиной 10 – 12 см и внутренним диаметром 2 - 4 мм. Лампа имеет накаливаемый катод 3 и анод 5. Газоразрядная криптоновая лампа помещается в сосуд Дьюара 6 с жидким азотом. Дьюаровский сосуд находится в герметически закрытой камере 7. Откачивая испаряющийся азот насосом, понижают температуру внутри сосуда и обеспечивают в камере условия, соответствующие тройной точке азота ( Излучение положительного столба газового разряда в направлении от катода к аноду выводится наружу через торец капилляра и направляется к компаратору. С помощью компаратора производится сличение эталонов длины с указанным выше числом длин волн света. Эталон метра, как и большинство эталонов, представляет собой сложный комплекс аппаратуры, требующий для своего обслуживания и применения ученых высочайшей квалификации. Государственный первичный эталон метра РФ включает:
а) источник излучения – газоразрядная лампа с изотопом криптона-86; б) эталонный интерферометр с фотоэлектрическим микроскопом и рефлектором для измерений длины в пределах 0¸1000 мм, снабженный платиновым термометром сопротивления и дифференциальными термопарами для точных измерений температуры; в) эталонный спектроинтерферометр для измерения длин волн в пределах 200¸3000 нм.
 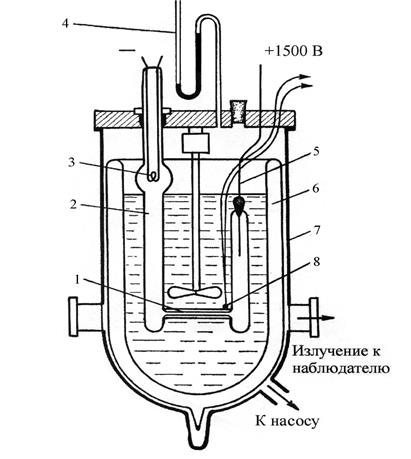
Рис. 1.20. Схема источника излучения эталона метра: 1 - капилляр; 2 - газоразрядная лампа; 3 - накаливаемый катод; 4 - манометр; 5 - анод; 6 - сосуд Дьюара; 7 - герметически закрытая камера; 8 - термопара; 9 - жидкий азот
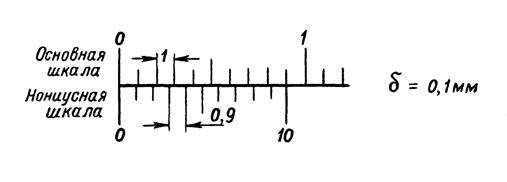
Место хранения Государственного эталона метра – ВНИИМ им. Д.И. Менделеева. Он обеспечивает воспроизведение единицы длины 1 м со средним квадратичным отклонением не более 5×10-9 м. Эталон метра постоянно совершенствуется в целях повышения точности, стабильности, надежности. Методы повышения точности базируются на возможности использования в качестве источников интенсивного монохроматического излучения с узкой спектральной линией стабилизированных лазеров и других физических эффектов. Под эгидой Международного бюро мер и весов производится систематическое международное сличение национальных эталонов крупнейших метрологических лабораторий с Международным эталоном и между собой. Эталоны метра сличают один раз в 25 лет. Нониусы На рис. 1.21-1.23 представлены в увеличенном виде различные типы нониусов. На основной шкале одно деление равно 1 мм, у каждого десятого штриха проставлено число, показывающее количество сантиметров, отсчитанных от нулевого штриха. Длина деления нониуса и отрезка на основной шкале, соизмеримого с делением нониуса, указаны в миллиметрах. Основными характеристиками нониусов являются точность нониуса (наименьшая величина отсчета по нониусу, цена деления нониуса) (1.14) Нониусы с точностью отсчета 0,1 мм изображены на рис. 1.21: а – модуль нониуса с = 1, десять делений нониуса имеют длину 9 мм, каждое деление нониуса равно 9 мм: 10 = 0,9 мм, т.е. короче деления основной шкалы на 1 мм – 0,9 мм = 0,1 мм; б – в растянутом нониусе (модуль нониуса с = 2) длина десяти его делений равна 19 делениям основной шкалы или 19 мм, каждое деление нониуса равно 19 мм: 10 = 1,9 мм, т.е. короче двух делений основной шкалы на 2 мм – 1,9 мм = 0,1 мм.
а
б
Рис. 1.21. Нониусы с точностью отсчета а – модуль нониуса с = 1; б – модуль нониуса с = 2 (растянутый нониус) Кроме нониусов с точностью 0,1 мм, применяются нониусы с точностью отсчета 0,05 и 0,02 мм.
б Рис. 1.22. Нониусы с точностью отсчета а – модуль нониуса с = 1; б – модуль нониуса с = 2 (растянутый нониус)
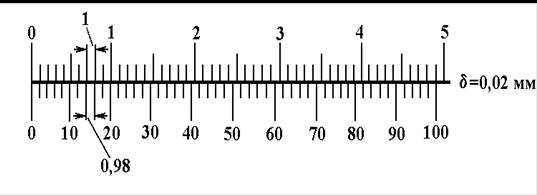
Нониус с точностью 0,02 мм и модулем с = 1 имеет 50 делений на длине 49 мм (рис. 1.23). В этом случае каждое деление нониуса равно 49 мм: 50 = 0,98 мм, т.е. короче деления основной шкалы на 1 мм – 0,98 мм = 0,02 мм.
Рис. 1.23. Нониус с точностью отсчета Иногда в приборах предусмотрен отсчет в двух противоположных направлениях. В этом случае не только основная шкала, но и нониусная шкала состоят из двух совершенно одинаковых шкал, расположенных по обе стороны от нулевого штриха; при отсчетах следует пользоваться той шкалой, которая идет вперед по направлению отсчетов. Добавочная шкала штангенинструмента, называемая нониусом, служит для повышения точности отсчета дробных долей миллиметра. Величина точности нониуса (0,1 мм; 0,05 мм или 0,02 мм) указана на рамке либо на штанге инструмента. Числа у штрихов нониуса проставлены для удобства отсчета долей деления основной шкалы. В некоторых случаях для облегчения отсчета нониусы снабжаются скрепленными с ними лупами. При отсутствии таковых рекомендуется пользоваться для отсчета обыкновенными ручными лупами.
Штангенциркули Штангенциркули, предназначенные для измерения наружных и внутренних размеров изделий, выпускаются четырех типов: ШЦ-I (рис. 1.8); ШЦТ-I (ШЦ-I – без верхних губок с нижними губками, выполненными из твердого сплава); ШЦ-II (рис. 1.24) и ШЦ-III (ШЦ-II без верхних губок) (рис. 1.26). Штангенциркуль ШЦ-II представлен на рис. 1.24.
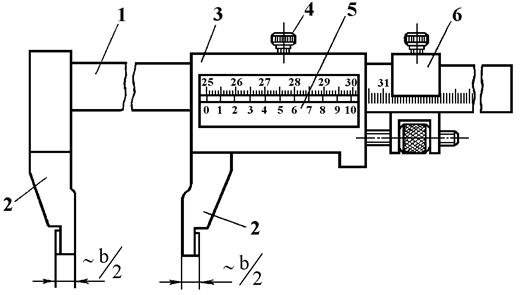
Рис. 1.24. Штангенциркуль ШЦ-II: 1 – штанга; 2 – измерительные ножки (губки); 3 – разметочные ножки (губки); 4 – рамка, 5 – зажим рамки; 6 – нониус; 7 – движок микрометрической подачи; 8 – зажим движка; 9 – винт; 10 – гайка
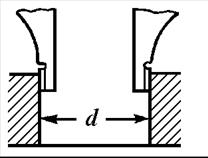
В конструкции этого инструмента имеются две пары измерительных ножек. Заостренные верхние ножки служат для наружных измерений и разметки. Каждая из измерительных нижних ножек имеет по две измерительные поверхности – внутреннюю (плоскую) и наружную (цилиндрическую). Две плоские поверхности, расположенные на внутренней стороне измерительных ножек, служат для наружных измерений. Две цилиндрические поверхности, расположенные на наружных сторонах измерительных ножек, служат для внутренних измерений (рис. 1.25). При измерении внутренних размеров ширина губок b прибавляется к отсчету.
Рис. 1.25. Измерение внутренних размеров штангенциркулем ШЦ-II
Для облегчения установки инструмента на заданный размер имеется устройство, состоящее из винта 9, гайки 10, движка 7 и зажима 8 (рис. 1.24). Резьба винта 9 имеет малый шаг, поэтому винт также принято называть микрометрическим. Микрометрический винт 9 жестко соединен с рамкой 4. Гайка 10 расположена в прорези движка 7. Микрометрическая подача рамки достигается при вращении гайки 10. Если движок 7 закрепить на штанге винтом 8 и вращать гайку 10, то микрометрический винт получит поступательное движение относительно гайки и движка. В результате рамка 4 с подвижной ножкой начнет перемещаться по штанге. При навинчивании гайки на винт ножки раздвигаются, при обратном ходе – ножки сдвигаются. Штангенциркули этого типа имеют пределы измерений 0 – 150, 0 – 200 и 0 – 300 мм. Штангенциркуль типа ШЦ-III изображен на рис. 1.26. В конструкции инструмента имеется одна пара измерительных ножек для наружных и внутренних измерений и микрометрическая подача рамки. Штангенциркули с односторонними ножками изготавливаются с верхними пределами измерений от 300 до 2000 мм.
Рис. 1.26. Штангенциркуль ШЦ-III: 1 – штанга; 2 – измерительные губки; 3 – рамка; 4 – зажим рамки; 5 – нониус; 6 – микрометрическая подача
Рис. 1.27. Штангенциркуль со стрелочным индикатором: 1 – штанга; 2 – подвижная рамка; 3 – индикатор
Рис. 1.28. Штангенциркуль с электронным цифровым отсчетом
Микрометры
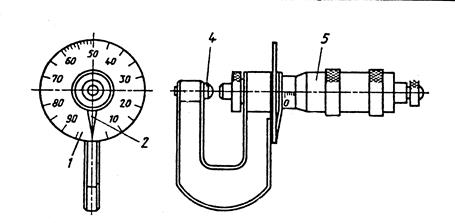
  Микрометры с циферблатом МЛ (рис. 1.29) применяют для измерения толщины листов и лент. К их отличительным особенностям относятся увеличенный вылет скобы 3, сферическая измерительная поверхность пятки 4, отсчетное устройство, выполненное в виде неподвижного циферблата 1 и стрелки 2, вращающейся вместе с барабаном 5. Микрометры с циферблатом МЛ (рис. 1.29) применяют для измерения толщины листов и лент. К их отличительным особенностям относятся увеличенный вылет скобы 3, сферическая измерительная поверхность пятки 4, отсчетное устройство, выполненное в виде неподвижного циферблата 1 и стрелки 2, вращающейся вместе с барабаном 5.

Рис. 1.29. Микрометр МЛ со стрелочным индикатором: 1 – неподвижный циферблат; 2 – стрелка; 3 – скоба; 4 – опорная пята; 5 – барабан
Микрометры с цифровым отсчетом показаний (рис. 1.30) повышают качество и производительность измерений. Числовой механизм может располагаться либо в стебле микровинта (а) либо в скобе микрометра (б).
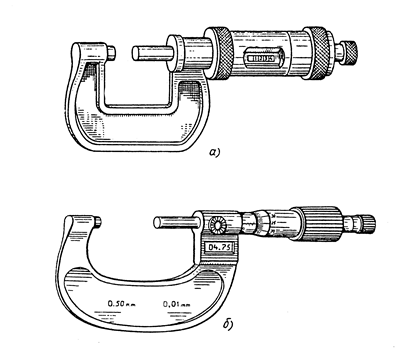
Рис. 1.30. Микрометры с электронным цифровым отсчетом
СПИСОК ЛИТЕРАТУРЫ 1. Агапов, Б.Т. Лабораторный практикум по физике / Б.Т. Агапов, Г.В.Максютин, П.И. Островерхов [Текст]. М.: Высшая школа, 1982. С. 50–55. 2. Ариас, Е.А. Сборник лабораторных работ по общему курсу физики: в 2 ч. Ч.1/Е.А. Ариас, З.С. Бондарева, Ф.А. Груздев [и др.] [Текст]. Великий Новгород: НовГУ им. Ярослава Мудрого, 2003. С.5–19. 3. Васильев, А.С. Основы метрологии и технические измерения / А.С. Васильев [Текст]. М.: Машиностроение, 1988. 239 с. 4. Детлаф, А.А. Курс физики / А.А. Детлаф, Б.М. Яворский [Текст]. М.: Высшая школа, 1989. С. 8–16. 5. Кабардин, О.Ф. Факультативный курс физики: 8 класс / О.Ф. Кабардин, В.А. Орлов, А.В. Пономарева [Текст]. М.: Просвещение, 1985. С. 4–18, 24–27. 6. Контрольно-измерительные приборы и инструменты / С.А. Зайцев, Д.Д. Грибанов [и др.] [Текст]. М.: Академия, 2003. С. 18–19, 62–67. 7. Кортнев, А.В. Практикум по физике / А.В. Кортнев, Ю.В. Рублев, А.Н. Куценко [Текст]. М.: Высшая школа, 1961. С. 30–34. 8. Лабораторный практикум по общей и экспериментальной физике: Учеб. пособие для студ. высш. пед. учеб. заведений / В.Н. Александров, С.В. Бирюков [и др.] / Под ред. Е.М. Гершензона и А.Н. Мансурова [Текст]. М.: Академия, 2004. С. 5–24. 9. Минчин, С.Н. Измерительный инструмент и техника измерений / С.Н. Минчин, А.Е. Шац [Текст]. М.: Оборонгиз, 1957. С. 8–43, 56–66. 10. Руководство к лабораторным занятиям по физике / Л.Л. Гольдин, Ф.Ф. Игошин [и др.] / Под ред. Л.Л. Гольдина [Текст]. М.: Наука, 1964. С. 34–40. 11. Физическая энциклопедия: в 5 т. Т.3 / Гл. ред. А.М. Прохоров [Текст]. М.: Большая Российская энциклопедия, 1992. С. 124. 12. Чертов, А.Г. Международная система единиц измерений / А.Г. Чертов [Текст]. М.: Высшая школа, 1967. С. 157–161.
ЛАБОРАТОРHАЯ РАБОТА2
ОПРЕДЕЛЕHИЕ МАССЫ ТЕЛА С ПОМОЩЬЮ ТЕХНИЧЕСКИХ ВЕСОВ
ЦЕЛИ РАБОТЫ
1. Изучение физических основ взвешивания на рычажных весах. 2. Изучение устройства и правил взвешивания на технических весах. 3. Определение массы тела с помощью технических весов. 4. Оценка абсолютной и относительной погpешностей пpи прямых измерениях массы тела. 5. Расчет плотности твердого тела правильной геометрической формы и оценка погрешностей при косвенных измеpениях.
ОСНОВНЫЕ ПОНЯТИЯ Среди многочисленных методов исследования весовой метод занимает особое место благодаря своей простоте, универсальности и достоверности. Весы являются одним из важнейших инструментов в неорганической и физической химии. Практически каждое физико-химическое исследование начинается взвешиванием. Весы и весовые дозаторы* используются в промышленном и сельскохозяйственном производствах в качестве основных средств количественного учета сырья и готовой продукции. Велика их роль в сфере потребления и обслуживания. Весоизмерительная и весодозировочная техника имеет большое значение для всех отраслей народного хозяйства и государства в целом. Главная цель работы – изучение физических основ взвешивания на рычажных весах.
Взвешивание и весы
Взвешиванием называют сравнение массы* данного тела с массой гирь, масса которых известна и выражена в определенных единицах (мг, г, кг и др.). Взвешивание тел производится с помощью весов. Весы – это прибор для определения массы тел по действующей на них силе тяжести. Весы являются важнейшим прибором в лаборатории. В зависимости от назначения весы делятся на образцовые (для проверки гирь), лабораторные (в том числе аналитические), специальные (пробирные, торзионные и др.) и общего назначения. По принципу действия весы подразделяются на рычажные, пружинные, крутильные, гидростатические, электротензометрические и др. По степени автоматизации цикла взвешивания – с автоматическим, полуавтоматическим и неавтоматическим уравновешиванием. В зависимости от точности**, с которой производят взвешивание, весы делятся на следующие группы: 1) для грубого взвешивания (точность до граммов); 2) для точного взвешивания: а) технические (точность до 10 мг); б) технохимические (точность до 1 мг); в) аналитические: - обычные (точность до 0,1 - 0,2 мг); - полумикрохимические (точность до 0,01 - 0,02 мг); - микрохимические (точность до 0,001 мг); - ультрамикрохимические (точность до 10-6 - 10-9 мг). Каждая из этих групп подразделяется на подгруппы в зависимости от конструктивных особенностей. Запись результатов взвешивания показывает, с какой точностью оно было сделано. Например, если масса тела записана «9,5 г», то это означает, что взвешивание было произведено на весах для грубого взвешивания; если масса тела записана «9,50 г» или «9,500 г» – взвешивание было произведено на технических или технохимических весах. Если же масса записана «9,5000 г», – взвешивание было произведено на аналитических весах. Следовательно, количество знаков после запятой должно показывать, с какой точностью и на каких весах было произведено взвешивание. Весы характеризуются наибольшим и наименьшим пределами взвешивания (тmax и тmin), т.е. значениями массы выше и ниже которых взвешивание невозможно или его погрешность может превысить допускаемое
______________________ * Масса – (лат. massa, букв. – глыба, ком, кусок) фундаментальная физическая величина, определяющая инерционные и гравитационные свойства материи (см. приложения 2.6.1, 2.6.2). ** Характеристики точности измерений массы в зависимости от ее величины и метода измерения приведены в приложении 2.6.3. значение. Наибольший предел взвешивания называется предельной нагрузкой, или грузоподъемностью весов.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.105.72 (0.016 с.) |

 , см
, см
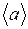 по формуле:
по формуле: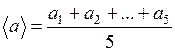 . (1.19)
. (1.19)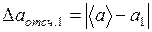 и т.д. (1.20)
и т.д. (1.20)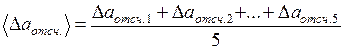 . (1.21)
. (1.21)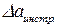 Найти границу абсолютной погрешности длины тела:
Найти границу абсолютной погрешности длины тела: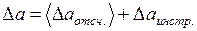 . (1.22)
. (1.22)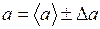 . (1.23)
. (1.23)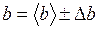 , (1.24)
, (1.24)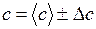 . (1.25)
. (1.25)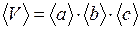 . (1.26)
. (1.26)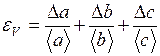 . (1.27)
. (1.27)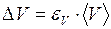 . (1.28)
. (1.28)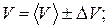
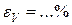 . (1.29)
. (1.29)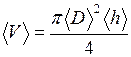 . (1.30)
. (1.30)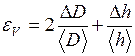 . (1.31)
. (1.31)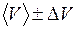 ;
; 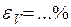 . (1.33)
. (1.33)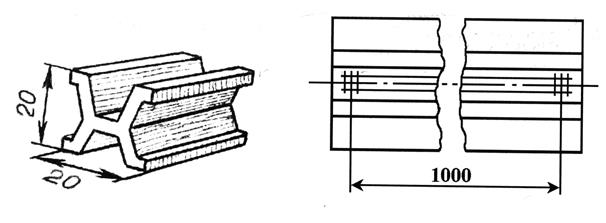
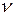 которого определяется из условия
которого определяется из условия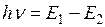 , (1.34)
, (1.34)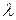 равна
равна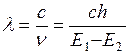 , (1.35)
, (1.35)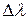 вблизи длины волны
вблизи длины волны 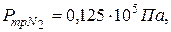
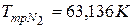 ). При температуре тройной точки азота газоразрядная лампа содержит твердую фазу криптона 86 (
). При температуре тройной точки азота газоразрядная лампа содержит твердую фазу криптона 86 (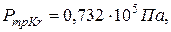
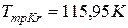 ). Температура капилляра измеряется термопарой 8, а давление паров азота – манометром 4. Плотность разрядного тока в капилляре должна быть (3±1)∙103 А/м2. При таком режиме работы обеспечивается достаточно высокая когерентность оранжевого излучения криптоновой лампы.
). Температура капилляра измеряется термопарой 8, а давление паров азота – манометром 4. Плотность разрядного тока в капилляре должна быть (3±1)∙103 А/м2. При таком режиме работы обеспечивается достаточно высокая когерентность оранжевого излучения криптоновой лампы.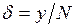 и модуль нониуса (1.15)
и модуль нониуса (1.15) 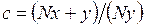 .
. При использовании растянутого нониуса (модуль нониуса с > 1) принцип определения размера детали, а также точность отсчета по нониусу не изменяются, но удобство отсчета увеличивается.
При использовании растянутого нониуса (модуль нониуса с > 1) принцип определения размера детали, а также точность отсчета по нониусу не изменяются, но удобство отсчета увеличивается.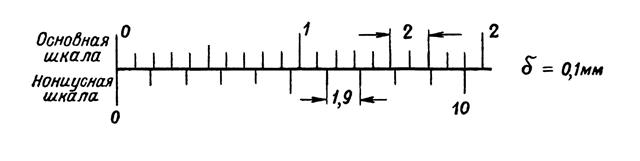
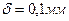 :
: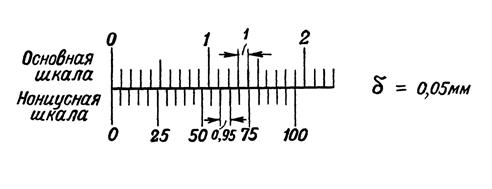 Нониусы с точностью 0,05 мм представлены на рис. 1.22: а – модуль нониуса с = 1, на шкале нониуса длиной 19 мм нанесено 20 делений, каждое деление нониуса равно 19 мм: 20 = 0,95 мм, т.е. короче деления основной шкалы на 1 мм – 0,95 мм = 0,05 мм; б – модуль нониуса с = 2, длина шкалы растянутого нониуса равна 39 делениям основной шкалы или 39 мм, каждое деление нониуса равно 39 мм: 20 = 1,95 мм, т.е. короче двух делений основной шкалы на 2 мм – 1,95 мм = 0,05 мм.
Нониусы с точностью 0,05 мм представлены на рис. 1.22: а – модуль нониуса с = 1, на шкале нониуса длиной 19 мм нанесено 20 делений, каждое деление нониуса равно 19 мм: 20 = 0,95 мм, т.е. короче деления основной шкалы на 1 мм – 0,95 мм = 0,05 мм; б – модуль нониуса с = 2, длина шкалы растянутого нониуса равна 39 делениям основной шкалы или 39 мм, каждое деление нониуса равно 39 мм: 20 = 1,95 мм, т.е. короче двух делений основной шкалы на 2 мм – 1,95 мм = 0,05 мм.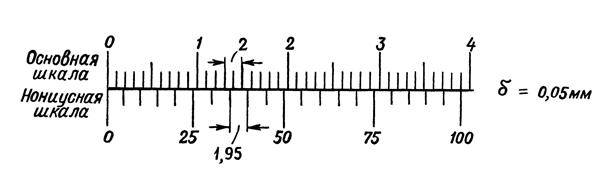 а
а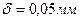 :
:
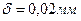
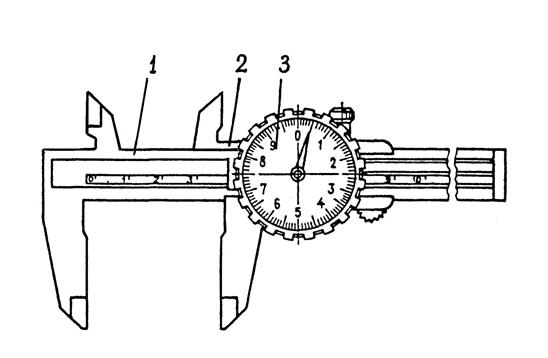 Штангенинструменты с автоматическим отсчетом показаний (рис. 1.27) повышают качество и производительность измерений. В штангу 1 индикаторного штангенциркуля вмонтирована зубчатая рейка. Зубчатое колесо индикатора 3, закрепленного на рамке 2 с подвижной губкой, перемещается по зубчатой рейке. Поворот зубчатого колеса преобразуется в перемещение стрелки индикатора. По шкале, нанесенной на штанге, отсчитывают десятки миллиметров, по шкале индикатора – единицы, десятые и сотые доли миллиметра.
Штангенинструменты с автоматическим отсчетом показаний (рис. 1.27) повышают качество и производительность измерений. В штангу 1 индикаторного штангенциркуля вмонтирована зубчатая рейка. Зубчатое колесо индикатора 3, закрепленного на рамке 2 с подвижной губкой, перемещается по зубчатой рейке. Поворот зубчатого колеса преобразуется в перемещение стрелки индикатора. По шкале, нанесенной на штанге, отсчитывают десятки миллиметров, по шкале индикатора – единицы, десятые и сотые доли миллиметра.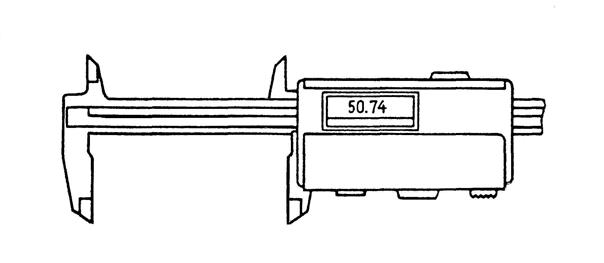 Штангенинструмент с электронным цифровым отсчетом показан на рис. 1.28.
Штангенинструмент с электронным цифровым отсчетом показан на рис. 1.28.