
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип взвешивания на рычажных весахСодержание книги
Поиск на нашем сайте
Главной частью рычажных весов является коромысло 1 (рис. 2.3).
Рис. 2.3. Коромысло равноплечих рычажных весов: 1 – коромысло; 2 – опорная подушка; 3 – опорная призма; 4 – грузоприемные призмы
Коромысло равноплечих весов является рычагом первого pода. В центре коромысла укреплена центральная опорная призма 3*, а по краям – две концевые грузоподъемные призмы 4. По конструкции весов рабочие pебpа призм АВ, CD и EF находятся в одной плоскости. Центральная призма опирается на плоскую подушку 2, неподвижно закрепленную на корпусе. Осью вращения (качания) коромысла весов является рабочее ребро CD опорной призмы. Принцип действия рычажных весов основан на уравновешивании действующего на коромысло весов момента силы веса груза, массу которого необходимо определить, моментом силы веса разновесов, масса которых известна.
Рис. 2.4. Коромысло весов с подвесками: 1 - коромысло; 2 - опорная подушка; 3 - опорная призма; 4 - грузоподъемные призмы; 5 - подушки подвесок; 6 - подвески с чашками; 7 - гиря; 8 - груз
К грузоподъемным призмам 4 через плоские подушки 5 подвешены симметричные подвески 6, горизонтальные участки которых служат площадками (чашками) для размещения груза 8 и гирь 7. К коромыслу жестко прикреплена стрелка, свободный конец которой перемещается относительно неподвижной шкалы (на рисунке не указаны). Рассмотрим уравновешенное ненагруженное коромысло весов (рис. 2.5). Для упрощения на рисунке изображено только коромысло весов, призмы и подушки. Точка О – это проекция на плоскость рисунка рабочего ребра центральной опорной призмы; в дальнейшем будем называть ее точкой опоры. Точки А и В – проекции на плоскость рисунка рабочих ребер грузоподъемных призм. При правильной установке весов в состоянии равновесия рабочие ребра призм находятся в горизонтальной плоскости. К грузоподъемным призмам в точках А и В приложены силы веса подвесок с чашками
Рис. 2.5. Равновесие нагруженного коромысла весов
Поместим на левую чашку тело массой т1. Коромысло весов выйдет из положения равновесия. Для того чтобы вернуть коромысло в первоначальное положение, необходимо на правую чашку накладывать разновески до тех пор, пока равновесие не восстановится. Пусть т2 – масса разновесок, уравновешивающих коромысло весов. Пренебрегая силой Архимеда, действующей на тела в среде (см. приложение 2.6.5), можно считать, что вес тела равен силе тяжести
вес разновесок равен
где Выберем ось Оz, совпадающую с осью вращения коромысла весов, поместив ее начало в точку опоры О. Если ось Оz направить за плоскость рис. 2.5, то проекция на эту ось моментов сил, вращающих рычаг по часовой стрелке, будет больше нуля; а проекция моментов сил, вращающих рычаг против часовой стрелки - меньше нуля. Момент суммарной силы реакции По условию равновесия тела, имеющего ось вращения, можно записать:
где
Подставив выражения (2.8) и (2.9) в равенство (2.7), получим:
Поскольку моменты сил веса левой и правой чашек ненагруженных весов предварительно уравновешены, то
и, следовательно, моменты сил веса груза
Для равноплечих весов l1 = l2, тогда при равновесии вес тела равен весу разновесок:
С учетом (2.5) и (2.6) получим
– при взвешивании на рычажных весах без учета влияния внешней среды сила тяжести
Тогда получим, что равные по весу тела в отсутствие влияния внешней среды имеют одинаковую массу:
Такое взвешивание называется простым. При простом взвешивании масса тела принимается равной массе разновесок (гирь). За истинное значение массы разновесок принимают их номинальное значение (см. п. 2.2.5). Рис. 2.6. Аптечные весы
Простейшим типом весов для простого взвешивания являются ручные, или аптечные, весы (рис. 2.6). Предельная нагрузка ручных весов может быть различной и достигает 100 г. Равновесие рычажных весов сохраняется вне зависимости от географической широты местности и высоты над уровнем моря. Примечание. Принцип взвешивания без применения гирь рассмотрен в Приложении 2.6.6.
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.73.46 (0.008 с.) |

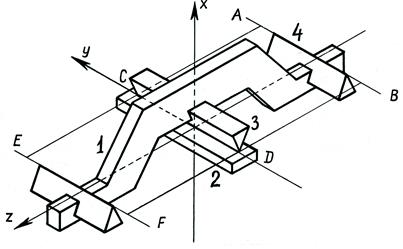
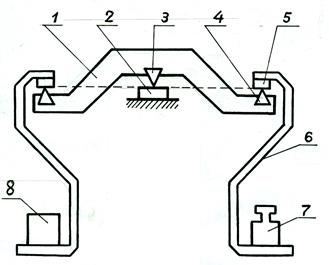 Схема коромысла с подвесками лабораторных равноплечих весов представлена на рис. 2.4 (обозначения 1–4 и назначение деталей коромысла весов те же, что и на рис. 2.3).
Схема коромысла с подвесками лабораторных равноплечих весов представлена на рис. 2.4 (обозначения 1–4 и назначение деталей коромысла весов те же, что и на рис. 2.3).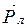 и
и 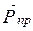 , направленные вертикально вниз. Обозначим расстояния от точки опоры до точек приложения сил веса:
, направленные вертикально вниз. Обозначим расстояния от точки опоры до точек приложения сил веса: 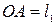 и
и 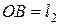 ; l1 – плечо силы
; l1 – плечо силы 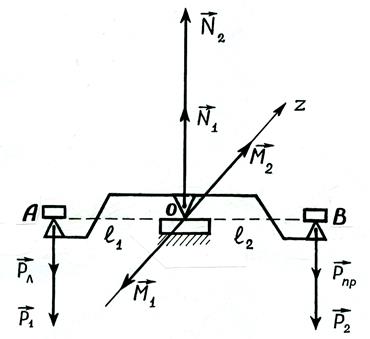 Сила реакции опоры
Сила реакции опоры 
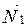 приложена в точке О к рабочему ребру центральной призмы и направлена вертикально вверх, уравновешивая две параллельные силы
приложена в точке О к рабочему ребру центральной призмы и направлена вертикально вверх, уравновешивая две параллельные силы 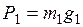 , (2.5)
, (2.5)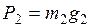 , (2.6)
, (2.6)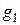 и
и 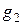 – ускорения свободного падения в местах расположения тела и разновесок.
– ускорения свободного падения в местах расположения тела и разновесок.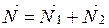 опорной подушки, действующей на центральную призму нагруженных весов, равен нулю, поскольку сила
опорной подушки, действующей на центральную призму нагруженных весов, равен нулю, поскольку сила 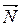 проходит через ось вращения и плечо этой силы равно нулю.
проходит через ось вращения и плечо этой силы равно нулю.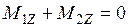 , (2.7)
, (2.7)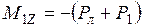 l1, (2.8)
l1, (2.8)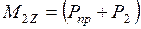 l2. (2.9)
l2. (2.9)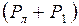 l1 =
l1 = 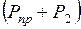 l2. (2.10)
l2. (2.10)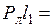
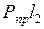 (2.11)
(2.11)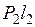 и веса разновесок
и веса разновесок 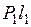 равны:
равны: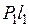 =
= 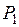 =
= 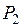 . (2.13)
. (2.13)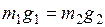 (2.14)
(2.14)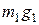 , с которой взвешиваемое тело притягивается к вращающейся Земле, сравнивается с силой тяжести
, с которой взвешиваемое тело притягивается к вращающейся Земле, сравнивается с силой тяжести 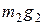 разновесок. Значения g в разных местах земной поверхности различны. Учитывая, однако, что тело и разновески находятся на очень близком расстоянии, ничтожно малой разницей между
разновесок. Значения g в разных местах земной поверхности различны. Учитывая, однако, что тело и разновески находятся на очень близком расстоянии, ничтожно малой разницей между 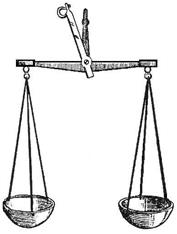
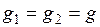 . (2.15)
. (2.15) . (2.16)
. (2.16)


