
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики точности измерения массыСодержание книги
Поиск на нашем сайте
в зависимости от ее величины и метода измерения* Общая картина современного состояния весоизмерительной техники по значениям предельных нагрузок и погрешностей определения массы для обычных (не суммирующих и не интегрирующих) весов представлена на рис. 2.13. По оси абсцисс (в логарифмическом масштабе) отложены значения предельных нагрузок, по оси ординат – приведенные значения погрешностей (отнесенные к соответствующему значению нагрузки, тоже в логарифмическом масштабе). График построен с учетом оптимальных условий использования весов и гирь – для каждой нагрузки используются соответствующие весы и гири.
Рис. 2.13. Погрешности измерения массы: 1 – сличение Государственного первичного эталона килограмма с Международным прототипом килограмма; 2 – метрологические исследования; 3 – аналитические исследования высшей точности; 4 – технические взвешивания повышенной точности, взвешивание драгоценных и токсичных материалов; 5 – торговые и хозяйственные взвешивания; заштрихованная область – взвешивание на автоматических, крановых и других технических весах и дозаторах.
Точка 1 характеризует наивысшую точность, которая достигается при сличениях эталонов килограмма. Кривая 2 дает представление о высшей точности определения массы, достижимой при метрологических работах («метрологическая точность»). Кривая 2 имеет минимум при нагрузке, равной 1 кг. Это объясняется тем, что в точке 1 передача значения единицы массы производится прямым сравнением с эталонами, в то время как при других нагрузках сказываются дополнительно погрешности, связанные с калибровкой гирь, воспроизводящих кратные или дольные значения килограмма. Как известно, с уменьшением предельной нагрузки весов абсолютные значения погрешностей быстро падают. Однако графики показывают, что, несмотря на это, происходит интенсивное возрастание приведенной погрешности измерений, что не может быть отнесено только за счет накопления погрешностей при калибровке гирь малых номиналов. В значительной мере это объясняется тем, что при малых нагрузках влияние внешних возмущений и сил трения сказывается в сравнительно большей степени, чем при больших нагрузках. Кривая 3 характеризует ту высшую точность определения массы, которая может быть достигнута в настоящее время при наиболее тщательном проведении исследовательских работ (за исключением метрологических). Кривая 4 дает представление о точности, регламентированной в России и ряде зарубежных стран, при взвешивании золота и других драгоценных металлов, а также токсичных материалов. Кривой 5 представлены допустимые погрешности весов общего назначения (настольных, платформенных, автомобильных и вагонных). Предельная нагрузка весов, достигнутая в мировой практике, составляет 500 т. Такие весы с классической рычажной схемой и несколькими грузоприемными платформами предназначены для определения положения центра тяжести и взвешивания сверхтяжелых самолетов. Минимальная предельная нагрузка серийно выпускаемых ультрамикровесов равна 10 мкг. Для специальных исследований применяются уникальные весы с предельными нагрузками порядка 1 мкг. Таким образом, отношение максимального и минимального пределов измерений массы с помощью весов составляет порядка 5 × 1014. Отношение точностей при взвешивании одной и той же нагрузки на весах разного назначения достигает 1 × 106.
Призма
Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. Призма называется правильной, если она прямая и основание ее – правильный многоугольник. Призма называется наклонной, если ее боковые ребра (грани) не перпендикулярны основаниям. Призма называется треугольной, если ее основание – треугольник, четырехугольной, если ее основание – четырехугольник, и вообще n - угольной, если основание ее – n -угольник. Призматическая поверхность – поверхность, образованная движением прямой в пространстве так, что эта прямая остается параллельной самой себе и пересекает данную ломаную линию. Рис. 2.14. Призма Подвижная прямая называется образующей призматической поверхности, а данная ломаная линия – ее направляющей.
Сила тяжести и вес тела
1. Если бы Земля не вращалась, то на тело массой т, лежащее неподвижно на опоре в вакууме, действовала бы гравитационная сила
Принимая для простоты, что Земля обладает сферической симметрией (по форме и плотности), можно записать гравитационную силу законом всемирного тяготения Ньютона:
где М = 5,96·1024 кг – масса Земли; R = 6,37·106 м – средний радиус Земли. . Притягиваясь к Земле, тело действует на подставку силой веса
Из уравнений (2.37)-(2.39) следует, что сила веса
и была бы направлена к центру Земли. При отсутствии опоры нет силы реакции
не зависящим от массы тела
и совпадающим по величине и направлению с вектором напряженности гравитационного поля в любой точке траектории.
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.137.96 (0.008 с.) |


 Призма – многогранник, полученный от пересечения призматической поверхности двумя параллельными плоскостями. Равные многоугольники (грани), полученные в сечении призматической поверхности с параллельными плоскостями, называются ее основаниями, а другие грани (параллелограммы) – боковыми гранями (рис. 2.14).
Призма – многогранник, полученный от пересечения призматической поверхности двумя параллельными плоскостями. Равные многоугольники (грани), полученные в сечении призматической поверхности с параллельными плоскостями, называются ее основаниями, а другие грани (параллелограммы) – боковыми гранями (рис. 2.14).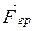 , направленная к центру Земли, а также сила реакции опоры
, направленная к центру Земли, а также сила реакции опоры 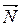 , направленная от центра Земли. В условиях равновесия
, направленная от центра Земли. В условиях равновесия . (2.37)
. (2.37) , (2.38)
, (2.38) – гравитационная постоянная;
– гравитационная постоянная; . По третьему закону Ньютона
. По третьему закону Ньютона . (2.39)
. (2.39) , действующая в вакууме со стороны покоящегося тела на опору или подвес на гипотетической невращающейся Земле, равнялась бы гравитационной силе
, действующая в вакууме со стороны покоящегося тела на опору или подвес на гипотетической невращающейся Земле, равнялась бы гравитационной силе 
 (2.40)
(2.40) , (2.41)
, (2.41) (2.42)
(2.42)


