
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние различных факторов на чувствительность весовСодержание книги
Поиск на нашем сайте Рассмотрим влияние различных факторов на чувствительность однорычажных коромысловых равноплечих весов. Для удобства и простоты целесообразно заменить достаточно сложную конфигурацию коромысла весов его упрощенной схемой (рис. 3.5). Точка О – проекция на плоскость рисунка рабочего ребра центральной опорной призмы; в дальнейшем будем называть ее точкой опоры. В точках А и В, соответствующих рабочим ребрам грузоподъемных призм, приложены силы веса Р чашек с грузом и разновесами
где т – масса нагрузки, Пунктир АОВ схематически изображает начальное положение плеч уравновешенного коромысла весов при грузах Р на чашках. Угол a – это угол между плечами коромысла и горизонталью MN. Центр тяжести коромысла находится в точке С, которая расположена ниже точки опоры О. Сила тяжести Обозначим: АО = ОВ = L – длина плеча коромысла, ОС = l – расстояние от точки опоры коромысла до центра тяжести.
Рис. 3.5. Равновесие нагруженного коромысла равноплечих весов
Допустим, что под действием дополнительного перегрузка массой ∆т и весом Проведем через точку О ось Oz перпендикулярно плоскости рис. 3.5 «на нас». Проекции на ось Oz моментов сил*, вращающих коромысло весов против часовой стрелки, положительны, а вращающих по часовой стрелке – отрицательны. Тогда на основании условия равновесия тела, имеющего ось вращения, можно записать для коромысла весов в положении А'ОВ':
После несложных преобразований** получим:
Разделив левую и правую части равенства (3.7) на D Р, получим выражение для чувствительности весов:
Для малых углов tg ∆a» Da, тогда
Из формулы (3.8) следует, что чувствительность весов, вообще говоря, зависит от общей нагрузки на чашках (2 Р + D Р) и не является постоянным параметром весов. Поскольку величина (2 Р + D Р) находится в знаменателе выражения (3.8), то при увеличении общей нагрузки чувствительность весов уменьшается. Влияние массы груза и разновесов на чувствительность весов необходимо исключить. Из выражения (3.9) следует, что это может быть достигнуто при условии, что опорные ребра всех трех призм коромысла лежат в одной горизонтальной плоскости и отсутствует деформация плеч коромысла, т.е. a = 0. В этом случае можно получить следующую формулу для чувствительности весов:
Выражение (3.10) показывает, что чувствительность весов уменьшается с увеличением расстояния от центра тяжести коромысла до точки опоры. Этой зависимостью пользуются для регулировки чувствительности большинства конструкций рычажных весов. На коромысле весов обычно имеются специальные грузики-гайки (на рис. 3.1 не указаны), которые могут перемещаться вверх или вниз по винтовой резьбе, что приводит к смещению центра тяжести коромысла со стрелкой, и, следовательно, к увеличению или уменьшению чувствительности весов. Чувствительность весов снижается при увеличении массы m 0коромысла. Поэтому коромысло весов, особенно высокочувствительных, изготавливается возможно более легким – обычно оно имеют ажурную форму, позволяющую совместить малую массу с повышенной жесткостью. Из формулы (3.10) следует также, что чувствительность весов повышается при увеличении размера коромысла, поскольку плечо L входит в числитель выражения. Однако на практике удлинение плеча коромысла неизбежно связано с увеличением массы, причем увеличение массы в большинстве случаев интенсивнее увеличения размеров. В результате эффект получается обратным – чувствительность падает. Добиться полного сведения рабочих ребер призм в одну горизонтальную плоскость практически не удается. Поэтому в конструкциях некоторых весов предусмотрена возможность регулировки положения призм и изменения в небольших пределах чувствительности. Чувствительность рычажных весов зависит не только от величин, входящих в аналитическое выражение (3.10), но и от ряда других факторов, не вошедших в это выражение: – от деформации коромысла при его нагрузке (при прогибе коромысла под действием нагрузки центр тяжести коромысла и точки приложения сил опускаются, что приводит к уменьшению чувствительности весов; поэтому профиль сечения коромысла выполняют возможно более жестким); – от установки призм; – от твердости призм и подушек и т.д. Методы точного взвешивания
Методы точного взвешивания применяют для исключения погрешностей, связанных с неравноплечестью коромысла при взвешивании на равноплечих весах. В большинстве случаев причиной неравноплечести является невозможность изготовления абсолютно симметричного коромысла. На изменение соотношения плеч коромысла влияет температура. Нагрев плеча коромысла на 0,1 – 0,20 С может вызвать удлинение плеча на несколько десятых долей микрометра (зависит от материала, из которого изготовлено коромысло). Погрешность из-за одностороннего нагрева плеча коромысла может многократно превышать цену деления аналитических весов. Причиной появления неравноплечести является установление груза и разновесов не в центре чашки, износ рабочих ребер призм и ряд других факторов. При рассмотрении методов точного взвешивания будем полагать, что коромысло весов предварительно уравновешено. 3.2.4.1. Метод двойного взвешивания (метод Гаусса)
а б Рис. 3.6. Равновесие нагруженного коромысла весов при двойном взвешивании: а – тело на левой чашке весов; б – тело на правой чашке весов Вследствие неравенства плеч результат первого взвешивания P 1 не будет совпадать с результатом Р 2 второго взвешивания и весом тела Р. Из условия равновесия при первом и втором взвешивании получим равенства:
где Р2: Р = Р: Р1, (3.12) тогда вес тела равен
– среднему пропорциональному, или среднему геометрическому из результатов двух взвешиваний. Этот метод взвешивания необходимо применять, например, при проверке разновесок. Из уравнений (3.11) и (3.12) можно найти отношение длин плеч коромысла весов (равноплечих по паспорту):
Поскольку результаты Р 1и Р 2мало отличаются друг от друга (| Р 2 – Р 1|<< P 1), то можно получить более простое выражение для быстрого расчета веса тела:
– вес тела равен среднему арифметическому из результатов взвешивания на левой и правой чашках весов. 3.2.4.2. Метод замещения (метод Борда)
Метод замещения – это взвешивание на одном плече весов. Иногда этот метод называют метод тарирования. На правую чашку весов помещают взвешиваемое тело, а на левую – тарный груз. Тарой называют предмет, уравновешивающий взвешиваемое тело. В качестве тары часто используют мелкую дробь, кусочки листового олова и т.д. Кусочки олова добавляют до тех пор, пока не будет достигнуто положение равновесия, точно совпадающее с нулевой точкой весов:
где РТ – вес тары. После этого тело снимают и на его место помещают такое количество разновесок, которое необходимо для уравновешивания тары:
где РР – вес разновесок. Из уравнений (3.17) и (3.18) следует, что вес тела равен весу разновесок: Р = РР. (3.19)
3.2.4.3. Метод максимальной нагрузки (метод Менделеева)
Метод принципиально не отличается от метода замещения – взвешивания на одном плече. Особенностью метода является постоянство массы на весах. Как уже было установлено, чувствительность и цена деления весов зависят от массы груза на чашках. Поэтому при изменении нагрузки, т.е. при замене гирь по номиналам, приходится каждый раз вновь определять цену деления весов. Предложение Менделеева позволяет определять цену деления только один раз, поскольку масса на весах остается постоянной, равной максимальной нагрузке весов. В этом методе на правую чашку весов помещают гири в количестве, соответствующем предельной нагрузке весов, а на левую – тару, точно уравновешивающую эти гири. Равновесия стараются достигнуть с возможной тщательностью. В этом случае
где РГ – вес гирь. Взвешиваемое тело помещают на чашку с гирями, снимая при этом столько гирь, чтобы весы были уравновешены:
Откуда следует, что вес тела равен весу снятых гирь ∆Р: Р = ∆Р. (3.22)
|
||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.011 с.) |

 , (3.5)
, (3.5) – ускорение свободного падения в месте расположения весов.
– ускорение свободного падения в месте расположения весов. уравновешенного коромысла весов действует по вертикали, проходящей через точку опоры О, где т0 - масса коромысла весов.
уравновешенного коромысла весов действует по вертикали, проходящей через точку опоры О, где т0 - масса коромысла весов.
 , помещенногона левую чашку весов, коромысло отклонилось на некоторый угол Da и заняло новое положение равновесия, изображенное на рис. 3.5 сплошной линией А'ОВ'.
, помещенногона левую чашку весов, коромысло отклонилось на некоторый угол Da и заняло новое положение равновесия, изображенное на рис. 3.5 сплошной линией А'ОВ'. . (3.6)
. (3.6) . (3.7)
. (3.7) .(3.8)
.(3.8) . (3.9)
. (3.9) . (3.10)
. (3.10) При использовании этого метода тело сначала помещают на левую чашку весов и момент силы веса тела уравновешивают моментом силы веса разновесов; затем тело помещают на правую чашку весов и повторяют уравновешивание (рис. 3.6, а, б).
При использовании этого метода тело сначала помещают на левую чашку весов и момент силы веса тела уравновешивают моментом силы веса разновесов; затем тело помещают на правую чашку весов и повторяют уравновешивание (рис. 3.6, а, б). ,
,  , (3.11)
, (3.11) и
и  - соответственно длины левого и правого плеч коромысла весов. Откуда
- соответственно длины левого и правого плеч коромысла весов. Откуда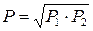 (3.13)
(3.13) . (3.14)
. (3.14) ; (3.15)
; (3.15) ;
; (3.16)
(3.16) , (3.17)
, (3.17) , (3.18)
, (3.18) , (3.20)
, (3.20) . (3.21)
. (3.21)


