Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нониус – многозначная мера длиныСодержание книги
Поиск на нашем сайте Представим себе две разномасштабные линейки. Сложим линейки вместе и совместим их нулевые штрихи, как показано на рис. 1.4. Пусть для определенности первая (верхняя) линейка имеет меньшие деления, длину одного деления обозначим х. Вторая (нижняя) линейка имеет большие деления, длина одного деления равна у. Поскольку деления линеек неодинаковы, то при совпадении нулевых штрихов первые штрихи не совпадают – они находятся друг от друга на некотором расстоянии По мере удаления от совпадающих нулевых штрихов расстояние между штрихами с одинаковыми номерами увеличивается.
Рис. 1.4. Две линейки, образующие нониус
Линейки образуют нониус, если существует такое целое число N, при котором выполняется равенство
Выражение (1.3) называют уравнением нониуса. Левая и правая части уравнения нониуса представляют собой расстояние между ближайшими совпадениями штрихов, выраженное через длину деления каждой из линеек. В результате деления левой и правой части уравнения нониуса на Nу получим, что меньшее деление составляет долю бо́льшего деления, равную
Точностью нониуса называется величина, равная разности делений линеек нониуса
Точность нониуса можно выразить через длину деления каждой из линеек:
Измерения с помощью нониуса Сравнивать длину детали с отрезками многозначной меры, концы которых нужно искать на двух неподвижно закрепленных как указано выше линейках, неудобно. Поступим иначе. Начнем медленно сдвигать вправо линейку нониуса с меньшими делениями. Нулевые штрихи разойдутся. Затем совпадут первые штрихи линеек. Это произойдет при сдвиге нулевых штрихов на величину ∆l, равную точности нониуса D N -ые штрихи, т.е. в этом случае т = N (см. рис. 1.4). Аналогичные наблюдения можно сделать при смещении нулевого штриха верхней линейки относительно первого штриха нижней линейки, затем относительно второго, третьего и т.д. В любом положении линеек нониуса один из штрихов верхней линейки (из первых N) совпадает с каким-либо штрихом нижней линейки или очень близко расположен к нему. Отсчет по нониусу основан на способности глаза фиксировать это совпадение. На практике линейку с малыми делениями делают обычно короткой, чтобы со штрихами второй линейки совпадал только один штрих этой линейки. Длинную линейку называют основной шкалой или масштабом, короткую – дополнительной шкалой, нониусом или верньером (по имени изобретателя – французского математика П. Вернье (1580-1637)). Рассмотрим процесс измерений с помощью нониуса. Пусть L – длина измеряемого образца (рис. 1.5). Совместим с началом образца нулевой штрих масштаба. Пусть при этом конец образца окажется между k -м и (k + 1)-м штрихами масштаба. Тогда в длине образца содержится k целых делений масштаба и отрезок
Рис. 1.5. Измерение длины детали с помощью нониуса
Для определения отрезка
Тогда вся длина будет равна
Результат можно сформулировать следующим образом: длина образца, измеряемая с помощью нониуса, равна длине целых делений масштаба до нулевого штриха нониуса плюс отрезок, равный произведению точности нониуса на номер штриха нониуса, совпадающего с некоторым штрихом масштаба. Погрешность, которая может возникнуть при таком методе отсчета, обусловлена неточным совпадением т -го штриха нониуса с (k + т)-м штрихом масштаба. Значение ее не будет превышать, очевидно, величину На рис. 1.6 изображен в увеличенном виде измерительный инструмент, у которого наименьшее деление масштаба у =
Рис. 1.6. Примеры измерений с помощью нониуса: а - L = 0,6 мм; б - L = 7,0 мм; в - L = 7,4 мм
Расширенный нониус Нониус не на всех приборах одинаков. Обычно в теории рассматривается случай, когда каждое деление нониуса на величину
где
На рис. 1.7 изображены в увеличенном виде основная шкала и расширенный нониус: наименьшее деление основной шкалы у = 1 мм; наименьшее деление нониуса х = 1,9 мм; отрезок основной шкалы, соизмеримый с наименьшим делением нониуса,
Рис. 1.7. Расширенный нониус
Точность расширенного нониуса можно найти из уравнения нониуса. Пусть N – число делений на нониусе, тогда длина линейки нониуса (всех его N делений) равна Nх. Длина линейки нониуса меньше длины такого же числа N отрезков масштаба
Выразив отсюда х и подставив в формулу (1.12), получим точность расширенного нониуса
- как N -ую долю наименьшего деления масштаба (ср. с формулой (1.7)). Модуль нониуса равен
Правила отсчета длины тела с помощью расширенного нониуса такие же, как и при использовании простейшего нониуса. Различные типы нониусов приведены в приложении 1.6.2. Нониусы используются в штангенциркулях, теодолитах, сахариметрах, препаратоводителях микроскопов и многих других приборах. Штангенциркуль
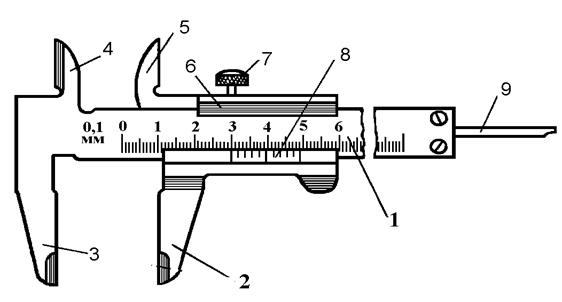
Штангенциркуль служит для измерений контактным способом линейных размеров тел, при которых не требуется высокая точность, т.е. с абсолютной погрешностью от 0,02 мм до 0,1 мм. Штангенциркуль предназначен для наружных и внутренних измерений, а также для измерения глубины или высоты выступа. Основной частью штангенциркуля (рис. 1.8) является масштабная линейка 1 или штанга, на которой нанесена миллиметровая шкала. Продольные грани штанги параллельны между собой. Вдоль штанги скользит подвижная рамка 6 с нониусом 8. Точность нониуса обычно указана на штанге. Положение рамки на штанге может быть зафиксировано с помощью винта 7.
Рис. 1.8. Штангенциркуль ШЦ–I: 1– штанга; 2 – подвижная нижняя ножка; 3 – неподвижная нижняя ножка; 4 – неподвижная верхняя ножка; 5 – подвижная верхняя ножка; 6 – рамка; 7 – винт для зажима рамки; 8 – нониус; 9 – линейка глубиномера
Неподвижная ножка (губка) 3 жестко скреплена (или составляет одно целое) со штангой и является упором. Измерительная поверхность ножки строго перпендикулярна продольным граням штанги. Подвижная рамка и подвижная ножка 2 также представляют одно целое. Рамка обеспечивает плавное передвижение подвижной ножки и ее устойчивое положение относительно штанги. Внутренние грани рамки плотно прилегают к наружным граням штанги – это обеспечивает параллельность измерительных поверхностей ножек, что очень важно при измерениях. Когда измерительные поверхности ножек соприкасаются, нулевой штрих нониуса совпадает с нулевым штрихом масштаба. Если измерительные поверхности не соприкасаются, то расстояние между ними равно расстоянию между нулевыми штрихами масштаба и нониуса. Штангенциркуль типа ШЦ-I с пределами измерений 0 – 125 мм (рис. 1.8) имеет две пары измерительных ножек. Две нижние ножки (2 и 3) служат для наружных измерений (рис. 1.9, а), а две верхние ножки (4 и 5) – для внутренних (рис. 1.9, б). Верхние ножки расположены так, что при измерении внутренних размеров отсчет ведется от нуля, т.е. так же, как и при измерении наружных размеров.
а б
Рис. 1.9. Измерение с помощью штангенциркуля Рис. 1.10. Измерение ШЦ-I: а – наружных размеров; б – внутренних размеров глубины отверстия
Штангенциркуль ШЦ-I снабжен глубиномером в виде линейки или стержня 9 (рис. 1.8), который жестко скреплен с подвижной рамкой. Если измерительные поверхности ножек соприкасаются (нулевые штрихи совпадают), то торец глубиномера совпадает с торцом штанги. При перемещении рамки линейка глубиномера выдвигается. На сколько нулевой штрих нониуса сдвинут относительно нулевого штриха масштаба, на столько же линейка глубиномера выступает за торец штанги. Линейка глубиномера применяется для измерения глубины или высоты выступа (рис. 1.10). Существует несколько видов штангенциркулей. Они отличаются типом и количеством измерительных ножек, длиной штанги, типом нониуса и наличием некоторых вспомогательных деталей (см. приложение 1.6.3).
|
||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

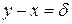 . Расстояние между вторыми штрихами равно
. Расстояние между вторыми штрихами равно  , расстояние между третьими штрихами равно
, расстояние между третьими штрихами равно  и т.д.
и т.д. Расстояние между штрихами с номером (т + 1) больше расстояния между штрихами с номером т на величину δ. Таким образом, две разномасштабные линейки являются многозначной мерой длины, с помощью которой можно реализовать отрезки, отличающиеся на величину
Расстояние между штрихами с номером (т + 1) больше расстояния между штрихами с номером т на величину δ. Таким образом, две разномасштабные линейки являются многозначной мерой длины, с помощью которой можно реализовать отрезки, отличающиеся на величину  .
. . (1.3)
. (1.3) . (1.4)
. (1.4)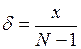 , (1.6)
, (1.6)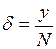 . (1.7)
. (1.7) Из формул (1.6) и (1.7) следует, что точность нониуса составляет
Из формул (1.6) и (1.7) следует, что точность нониуса составляет  долю меньшего деления либо
долю меньшего деления либо  долю бо́льшего деления линеек. Чем больше N, тем меньше эта доля.
долю бо́льшего деления линеек. Чем больше N, тем меньше эта доля.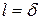 . Вторые штрихи линеек совпадут при сдвиге нулевых штрихов на две точности нониуса D
. Вторые штрихи линеек совпадут при сдвиге нулевых штрихов на две точности нониуса D 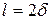 и т.д. Если совпали
и т.д. Если совпали 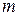 -е штрихи, то можно утверждать, что нулевые штрихи сдвинуты на D
-е штрихи, то можно утверждать, что нулевые штрихи сдвинуты на D 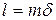 . При сдвиге ровно на одно большое деление
. При сдвиге ровно на одно большое деление 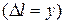 нулевой штрих верхней линейки совпадает с первым штрихом нижней линейки и совпадают
нулевой штрих верхней линейки совпадает с первым штрихом нижней линейки и совпадают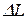 – неизвестная пока еще доля (k +1)-го деления масштаба:
– неизвестная пока еще доля (k +1)-го деления масштаба: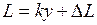 . (1.8)
. (1.8)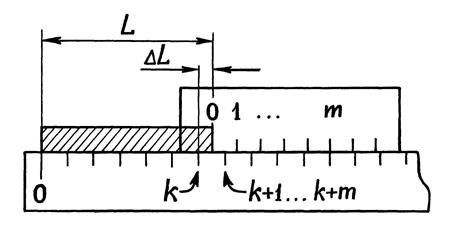
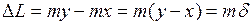 . (1.9)
. (1.9)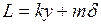 . (1.10)
. (1.10)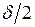 , ибо при большем несовпадении этих штрихов, один из соседних штрихов нониуса (справа или слева) имел бы несовпадение меньше
, ибо при большем несовпадении этих штрихов, один из соседних штрихов нониуса (справа или слева) имел бы несовпадение меньше 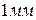 , наименьшее деление нониуса
, наименьшее деление нониуса 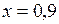 мм, точность нониуса
мм, точность нониуса 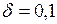 мм, N = 10. Из рисунка видно, что расстояние между нулевыми штрихами масштаба и нониуса в случае «а» равно 0,6 мм, в случае «б» – 7,0 мм, в случае «в» – 7,4 мм.
мм, N = 10. Из рисунка видно, что расстояние между нулевыми штрихами масштаба и нониуса в случае «а» равно 0,6 мм, в случае «б» – 7,0 мм, в случае «в» – 7,4 мм.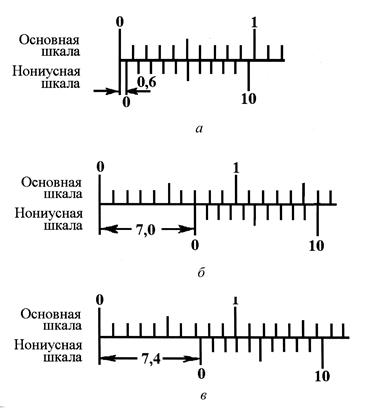
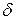 меньше одного наименьшего деления масштаба. Однако на практике для удобства измерений нониус «растягивают» так, чтобы каждое его деление было на величину
меньше одного наименьшего деления масштаба. Однако на практике для удобства измерений нониус «растягивают» так, чтобы каждое его деление было на величину 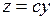 , (1.11)
, (1.11)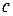 – целое число, которое называется модулем нониуса. Такой нониус называют расширенным или растянутым. Точность расширенного нониуса равна разности отрезка
– целое число, которое называется модулем нониуса. Такой нониус называют расширенным или растянутым. Точность расширенного нониуса равна разности отрезка 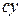 масштаба и наименьшего деления нониуса
масштаба и наименьшего деления нониуса 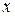
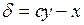 . (1.12)
. (1.12)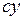 = 2 мм, модуль нониуса с = 2; число делений на нониусе N = 10; точность нониуса
= 2 мм, модуль нониуса с = 2; число делений на нониусе N = 10; точность нониуса 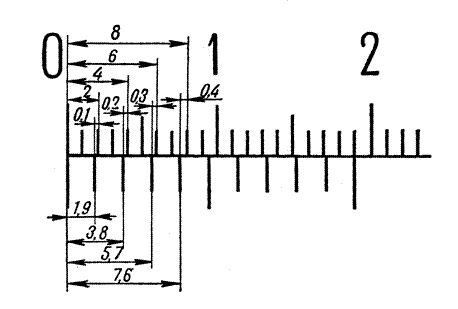
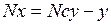 . (1.13)
. (1.13)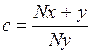 . (1.15)
. (1.15)