
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение плотности тела правильной геометрической формыСодержание книги
Поиск на нашем сайте
Плотность вещества* можно определить различными методами, используя зависимости свойств вещества от плотности. Наиболее распространенный метод определения плотности твердых тел основан на определении массы т и объема V тела. Определив массу и объем тела, можно найти значение плотности 1. Вписать в табл. 2.5 результаты измерений массы тела (табл. 2.4) и объема тела (см. лабораторную работу «Определение линейных размеров и объема тела правильной геометрической формы»), абсолютные и относительные погрешности. 2. Зная массу и объем тела, рассчитать плотность вещества при комнатной темпеpатуpе:
3. Определить относительную погрешность плотности по формуле:
4. Определить абсолютную погрешность плотности по формуле:
Результаты расчетов также внести в табл. 2.5 и представить в виде
5. Определить, из какого вещества изготовлено тело. Таблица 2.5
ТЕХНИКА БЕЗОПАСНОСТИ На рабочем месте могут находиться только необходимые в данной работе приборы и оборудование.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Каково устройство технических весов? 2. Какова последовательность подготовки весов к работе? 3. Каковы правила взвешивания на технических весах? 4. Что такое чувствительность весов? Как определить чувствительность ненагруженных весов? Нагруженных весов? 5. Как определить цену деления ненагруженных весов? Нагруженных весов? 6. Как рассчитать абсолютную погрешность массы тела при взвешивании на технических весах? 7. Что такое масса? Масса инертная, масса гравитационная? 8. Каковы представления о массе в классической механике Ньютона? В механике Эйнштейна? 9. Что называется плотностью? Средняя плотность тела, плотность в точке? Что такое элементарный объем?
10. Как зависит плотность вещества от температуры? Какова плотность воды при температуре 4°С и нормальном атмосферном давлении? Какова температурная зависимость плотности воды? 11. Что такое взвешивание? Как подразделяются весы по их назначению? По принципу действия? По точности измерений? 12. Что такое наибольший и наименьший пределы взвешивания весов? 13. Каковы отличительные особенности весов для точного взвешивания? 14. Что такое точный разновес? Номинальная масса гири? 15. Какая физическая величина называется моментом силы относительно точки? Как направлен вектор момента силы? Что такое плечо силы? 16. Что такое момент силы относительно оси? 17. Каково условие равновесия тела, имеющего ось вращения? 18. Каков принцип действия рычажных весов? 19. С какой целью весы устанавливают по отвесу (или по уровню)? Почему такая установка называется правильной? 20. Как изменится плечо силы веса подвески, действующей на коромысло весов, если груз расположить не в центре чашки? 21. В каких системах отсчета и с какой целью вводят силы инерции? 22. Является ли система отсчета, связанная лабораторией, находящейся на поверхности Земли, инерциальной? 23. Какие силы действуют на тело, покоящееся во вращающейся системе отсчета? 24. Что такое сила тяжести? Каково статическое проявление силы тяжести? Какова величина и направление силы тяжести? 25. Что такое вес тела? 26. Как зависит вес тела на Земле от широты местности? 27. Как зависит вес тела от окружающей среды? 28. Какие силы действуют на тело, движущееся во вращающейся системе отсчета? 29. Что такое сила Кориолиса? Как направлена сила Кориолиса? Какова ее величина? 30. Каково ускорение свободного падения тела на вращающейся Земле? Каково ускорение тела в начале свободного падения из состояния покоя? 31. Каков принцип взвешивания на пружинных весах? 32. Укажите факторы, влияющие на результат измерения массы с помощью пружинных весов? 33. Почему при решении многих практических задач Землю можно считать инерциальной системой отсчета?
Вопросы для допуска: 1-7. Вопросы для защиты: 8-33.
ПРИЛОЖЕНИЕ Масса тела Физическое представление о массе тела было заложено еще И. Ньютоном.
Масса материального тела – фундаментальная физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные и гравитационные свойства. Инертная масса В принципе ниоткуда не следует, что масса тела
где k – коэффициент пропорциональности. В системе единиц измерения СИ коэффициент k = I, следовательно, массы
Этот фундаментальный закон природы называют принципом эквивалентности. Ввиду того, что равенство инертной и гравитационной масс имеет важное значение, оно было весьма тщательно проверено в различных экспериментах. Можно считать доказанным, что эти массы равны друг другу с точностью, не меньшей, чем 10-12 их величины, т.е. В классической механике Ньютона считается, что: 1) масса - мера количества вещества, является одной из характеристик тела, она зависит от размеров тела и от природы вещества; 2) масса тела равна сумме масс всех частиц, из которых оно состоит (аддитивность массы); 3) масса закрытой системы (отсутствует обмен веществом с окружающей средой) не изменяется ни при каких процессах, происходящих в системе (закон сохранения массы); 4) масса тела не зависит от скорости его движения в системе отсчета. В механике Эйнштейна показано, что: 1) масса тела зависит от скорости
где т - масса движущегося тела,
т0 – масса покоя или масса тела, которой оно обладает при с = 3·108 м/с – скорость света в вакууме; 2) масса определяет запас полной энергии Е материального тела:
Поскольку при обычных скоростях Примечание. При определении массы макроскопических тел взвешиванием нет необходимости отступать от классических представлений, поскольку расхождение результатов определения массы, полученных на основе теории относительности Эйнштейна и классической механики Ньютона, значительно меньше точности, предъявляемой практикой. 2.6.2. Единица массы – килограмм
В системе СИ масса является основной физической величиной. Единица массы в СИ – килограмм. Килограмм есть масса эталонной гири из сплава иридия с платиной, хранящейся в Севре (Франция) в Международном бюро мер и весов. «Килограмм – единица массы – представлен массой международного прототипа килограмма» (ГОСТ 9867 – 61). Такое определение единицы массы было дано III Генеральной конференцией по мерам и весам в 1961 г.
При установлении метрической системы мер единицу массы было предложено вывести из единицы длины, приняв за нее массу воды, содержащуюся в кубе, размеры которого составляют определенную долю этой единицы длины. За единицу массы была принята масса одного кубического дециметра дистиллированной воды при температуре +4°С, при которой вода имеет наибольшую плотность. На основе такого определения был изготовлен образец килограмма – платиново-иридиевый цилиндр с высотой, равной своему диаметру 39 мм. Этот образец, как и образец метра, были переданы на хранение в Национальный архив Франции и с тех пор носят название архивного метра и архивного килограмма. В 1799 году они были специальным законом признаны окончательными прототипами метра и килограмма. Более поздние и более точные измерения показали, что масса 1 дм3 воды на 0,028 г меньше архивного прототипа килограмма и что взвешивание платиново-иридиевого цилиндра можно произвести примерно в тысячу раз точнее, чем определить массу кубического дециметра воды. В связи с этим Российская Академия наук поставила вопрос о признании основами метрической системы мер архивных метра и килограмма. Поскольку архивные метр и килограмм имели ряд недостатков, то было предложено изготовить новые их копии, которые, будучи им равны, позволяли бы выполнять с их помощью более точные измерения и как можно меньше изменялись бы во времени. По решению Международной комиссии по эталонам метрической системы (1872 г.) из платиново-иридиевого сплава (90% Pt, 10% Ir) были изготовлены эталоны килограмма. Один из них, масса которого наиболее точно соответствовала массе архивного килограмма, был принят за Международный прототип. Сличение с ним национальных эталонов килограмма в настоящее время производится с относительной погрешностью 2·10-9. Такая точность более и менее удовлетворяет требованиям современной науки и техники. Однако принятая единица массы метрической системы имеет ряд недостатков, неизбежных при таком искусственном ее определении. Во-первых, Международный прототип килограмма подвержен разрушению, что может вызвать потерю точности не только при измерениях массы, но и при измерениях других величин, в определение которых входит масса. Во-вторых, он невоспроизводим, что является недостатком как при его разрушении, так и при измерениях масс с наивысшей точностью, поскольку такие измерения можно выполнить только при наличии прототипа.
В-третьих, Международный прототип килограмма подвержен механическому износу даже при самом тщательном и осторожном обращении с ним. Кроме того, платиноиридий, из которого он изготовлен, как и любое вещество, испаряется. Небольшие потери в массе прототипа в результате этих причин в настоящее время еще не обнаружены, но они, несомненно, существуют и со временем будут вызывать систематические погрешности не только при измерении массы, но и при измерениях других величин, в определении которых входит масса. В дальнейшем может возникнуть потребность производить сличение эталонов с более высокой точностью. Поэтому ведутся работы по изысканию методов сравнения эталонов килограмма с атомными константами, например, с массой протона. Эта задача очень трудная и потребует для своего решения значительного времени. К сожалению, в настоящее время точность измерения атомных масс уступает точности измерения путем взвешивания. Государственный первичный эталон килограмма РФ хранится во ВНИИМ им. Д.И. Менделеева. В состав Государственного первичного эталона РФ входят: а) копия международного прототипа килограмма – платиново-иридиевый прототип № 12, представляющий собой гирю в виде цилиндра с закругленными ребрами диаметром 39 мм и высотой 39 мм; б) эталонные весы № 1 и № 2 на 1 кг с дистанционным управлением для передачи размера единицы массы от прототипа № 12 эталонам-копиям и от эталонов-копий рабочим эталонам. Национальные эталоны массы один раз в 25 лет сличают между собой и с Международным прототипом килограмма. Примечание. Международный Комитет Мер и Весов на 94-й Конференции в октябре 2005 года принял Рекомендацию по подготовительным шагам к переопределению четырех основных единиц СИ – килограмма, ампера, кельвина и моля, чтобы эти единицы были связаны со значениями фундаментальных физических констант, соответственно, постоянной Планка h, элементарного заряда е, постоянной Больцмана k и постоянной Авогадро NA.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.161.182 (0.012 с.) |

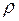 . Объем тела правильной геометрической формы можно определить, измерив линейные pазмеpы тела.
. Объем тела правильной геометрической формы можно определить, измерив линейные pазмеpы тела.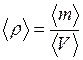 . (2.28)
. (2.28)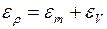 . (2.29)
. (2.29)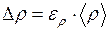 . (2.30)
. (2.30)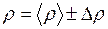 ;
; 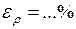 . (2.31)
. (2.31)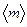 , г
, г
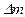 , г
, г
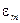 , %
, %
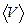 , см3
, см3
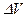 , см3
, см3
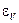 , %
, %
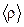 , г/ см3
, г/ см3
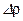 , г/ см3
, г/ см3
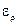 , %
, %
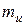 входит во второй закон Ньютона и характеризует динамические свойства тела. Инертность проявляется в том, что изменение состояния покоя или движения тела происходят не мгновенно, а постепенно. Скорость тела изменяется тем медленнее, чем больше его инертная масса. Гравитационная масса
входит во второй закон Ньютона и характеризует динамические свойства тела. Инертность проявляется в том, что изменение состояния покоя или движения тела происходят не мгновенно, а постепенно. Скорость тела изменяется тем медленнее, чем больше его инертная масса. Гравитационная масса 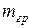 входит в закон всемирного тяготения Ньютона и выступает как источник поля тяготения. Каждое тело создает поле тяготения, характеристики которого пропорциональны массе
входит в закон всемирного тяготения Ньютона и выступает как источник поля тяготения. Каждое тело создает поле тяготения, характеристики которого пропорциональны массе 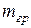 тела. С другой стороны, на каждое тело действует поле тяготения со стороны других тел. Это действие зависит от массы
тела. С другой стороны, на каждое тело действует поле тяготения со стороны других тел. Это действие зависит от массы 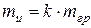 , (2.32)
, (2.32)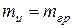 . (2.33)
. (2.33)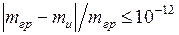 . Поэтому их не разделяют и говорят просто о массе тела т.
. Поэтому их не разделяют и говорят просто о массе тела т.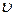 его движения, т.е. зависит от выбора системы отсчета, и характеризует не только количество материи, но и ее движение:
его движения, т.е. зависит от выбора системы отсчета, и характеризует не только количество материи, но и ее движение: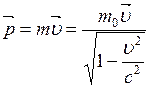 , (2.34)
, (2.34)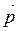 - импульс тела;
- импульс тела;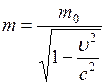 ; (2.35)
; (2.35)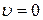 ;
;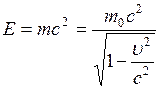 . (2.36)
. (2.36)


