
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однако земля вращается в системе неподвижных звезд и является поэтому неинерциальной системой отсчета.Содержание книги
Поиск на нашем сайте
В неинерциальной системе отсчета на каждую материальную точку (тело) действует сила инерции
Знак «минус» показывает, что сила инерции направлена в сторону, противоположную вектору ускорения Величина силы инерции зависит от расстояния r до оси вращения. Это расстояние зависит от географической широты
и на различных широтах разное – на экваторе оно наибольшее (j = 0), а на полюсе равно нулю ( На широте
где
а б Рис. 2.15. Сила инерции во вращающейся системе отсчета «Земля»
Рассмотрим более детально силы, действующие на тело, которое покоится на поверхности вращающейся Земли на некоторой широте
Из равенства (2.46) следует, что сила реакции Геометрическая сумма гравитационной силы
Тогда условие (2.46) равновесия тела имеет вид:
Вес тела
 
а б Рис. 2.16. Силы, действующие на тело и опору (а); на тело и подвес (б)
Таким образом, на вращающейся Земле в отсутствие среды вес
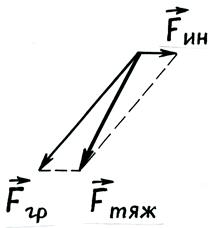
т.е. вес равен геометрической сумме гравитационной силы Определим величину силы тяжести и вес тела, находящегося в произвольной точке земной поверхности на широте φ. Из треугольника сил (рис. 2.17) следует
Рис. 2.17. Силы, действующие на тело и опору, покоящиеся во вращающейся системе отсчета «Земля»
С учетом выражений (2.38) и (2.45), получим
Таким образом, вес тела и сила тяжести зависят от массы тела т, от параметров, характеризующих Землю (М,ω), и от положения тела на Земле (R,φ). На полюсах
На экваторе (
Если учесть, что полярный и экваториальный радиусы Земли не одинаковы (Rпол = 6356, 9 км, Rэкв = 6378,1 км), то
После подстановки в формулу (2.55) значений Rпол, Rэкв, М, γ, а также
Таким образом, с учетом различия полярного и экваториального радиусов и вращения Земли вес тела и сила тяжести на экваторе уменьшаются примерно на 1,0 % от величины на полюсе! Определим теперь направление силы тяжести и веса тела. Сила тяжести и вес тела направлены к центру Земли только на полюсах и на экваторе. В остальных точках земной поверхности такого совпадения нет. Угол отклонения ∆α от направления на центр Земли зависит от географической широты φ. Поскольку угол ∆α мал, то из рис. 2.17 следует, что для сферической Земли
и для φ = 45° ∆α ≈ 0,1 °. Таким образом, если не требуется высокая точность, то приближенно можно считать, что сила тяжести и вес тела направлены к центру Земли и равны по модулю гравитационной силе. 3. В связи с актуальностью взвешивания объектов в движении необходимо рассмотреть влияние силы Кориолиса. Сила Кориолиса обусловлена движением тел относительно вращающейся системы отсчета. Сила Кориолиса зависит от скорости Выражение для кориолисовой силы имеет вид:
где Величина силы Кориолиса равна
где β – угол между векторами Сила Кориолиса равна нулю, если скорость движения тела равна нулю или угол между векторами
а б Рис. 2.18. Сила Кориолиса, действующая на тело, движущееся во вращающейся системе отсчета «Земля»
Если тело покоится относительно Земли, то
Таким образом, силе тяжести можно дать другое толкование, отказавшись от выражения (2.47)
Полученное выражение совпадает с выражением (2.47) для статического проявления силы тяжести при условии Ускорение свободного падения
Таким образом, ускорение свободного падения тела
Однако поскольку относительная ошибка
при скорости тела
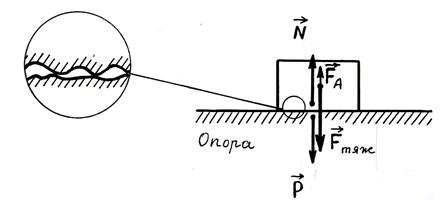
где 4. Вес тела зависит от окружающей среды. Вес тела в воздухе (или в жидкости) меньше, чем в безвоздушном пространстве, так как этих средах на тело действует выталкивающая сила. Возникновение выталкивающей силы можно объяснить тем, что соприкасающиеся поверхности тела и опоры не являются идеально гладкими – они имеют шероховатости (выступы), форма и величина которых различны. Фактически касание, т.е. реальный контакт поверхностей двух тел, происходит лишь в отдельных «пятнах» (рис. 2.19). Суммарная фактическая площадь касания составляет 0,001¸0,01 номинальной площади поверхности и зависит от природы тел и характера обработки их поверхности. Таким образом, тело, находящееся в среде, фактически окружено этой средой.
Рис. 2.19. Выталкивающая сила
На тело, находящееся в газовой среде, действует выталкивающая сила, равная произведению его объема на плотность среды и на ускорение свободного падения:
где
- плотность газовой среды, которая зависит от давления газа Сила реакции опоры В условиях равновесия
Откуда вес тела равен
Таким образом, вес тела в воздухе меньше силы тяжести. Вес тела является переменной величиной - зависит от температуры, давления и состава окружающей его газовой среды, а также от объема тела и ускорения свободного падения в месте нахождения тела. Расчет показывает, что уменьшение веса латунной гири массой т и плотностью
от силы тяжести. Если не требуется такая высокая точность, то можно полагать, что вес тела в воздухе равен силе тяжести:
Расчет поправки при определении массы на действие силы Архимеда приведен в п. 3.2.8.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.247.50 (0.009 с.) |

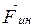 , которая является не результатом взаимодействия тел, а результатом ускоренного движения системы отсчета. Сила инерции равна произведению массы т материальной точки (тела) на ускорение
, которая является не результатом взаимодействия тел, а результатом ускоренного движения системы отсчета. Сила инерции равна произведению массы т материальной точки (тела) на ускорение  системы отсчета:
системы отсчета: . (2.43)
. (2.43)
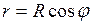 (2.44)
(2.44) ).
). сила инерции равна
сила инерции равна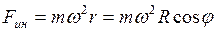 , (2.45)
, (2.45) – угловая скорость вращения Земли.
– угловая скорость вращения Земли.
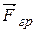 , направленная к центру Земли, и сила инерции
, направленная к центру Земли, и сила инерции  , направленная от оси ее вращения. Сила реакции опоры
, направленная от оси ее вращения. Сила реакции опоры  удерживает тело в неподвижном относительно Земли состоянии. Поскольку тело покоится в системе отсчета, то действующие на тело силы скомпенсированы
удерживает тело в неподвижном относительно Земли состоянии. Поскольку тело покоится в системе отсчета, то действующие на тело силы скомпенсированы . (2.46)
. (2.46) и инерции
и инерции  . Линия действия силы реакции
. Линия действия силы реакции 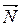 совпадает с линией действия результирующей двух сил
совпадает с линией действия результирующей двух сил  +
+  и силы инерции
и силы инерции  , учитывающей суточное вращение Земли, называется силой тяжести
, учитывающей суточное вращение Земли, называется силой тяжести  , действующей на неподвижное тело (рис. 2.15, б):
, действующей на неподвижное тело (рис. 2.15, б): . (2.47)
. (2.47) +
+  = 0. (2.48)
= 0. (2.48) – это сила, с которой любое тело, находящееся в поле силы тяжести, действует на опору или подвес, препятствующие свободному падению тела (рис. 2.16). Силы
– это сила, с которой любое тело, находящееся в поле силы тяжести, действует на опору или подвес, препятствующие свободному падению тела (рис. 2.16). Силы  и
и 


 (2.47):
(2.47):
 . (2.51)
. (2.51)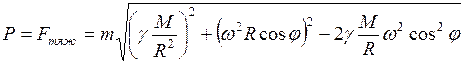 . (2.52)
. (2.52) вес тела и сила тяжести оказываются наибольшими и равными гравитационной силе
вес тела и сила тяжести оказываются наибольшими и равными гравитационной силе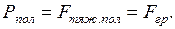 (2.53)
(2.53) ,
,  ) вес тела и сила тяжести принимают наименьшее значение
) вес тела и сила тяжести принимают наименьшее значение (2.54)
(2.54) . (2.55)
. (2.55) получим
получим
 %.
%.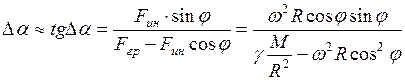 (2.56)
(2.56)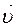 движения тела относительно системы отсчета и угловой скорости
движения тела относительно системы отсчета и угловой скорости  системы отсчета.
системы отсчета. , (2.57)
, (2.57)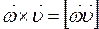 – векторное произведение.
– векторное произведение. , (2.58)
, (2.58) . Вектор
. Вектор  перпендикулярен плоскости, в которой лежат векторы
перпендикулярен плоскости, в которой лежат векторы  при движении по поверхности Земли вдоль параллели; на рис. 2.18 а, б представлен случай движения тела на восток).
при движении по поверхности Земли вдоль параллели; на рис. 2.18 а, б представлен случай движения тела на восток).
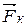 = 0 и действующие на него силы
= 0 и действующие на него силы 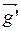 – динамическое проявление силы тяжести на вращающейся Земле. Уравнение движения тела имеет вид:
– динамическое проявление силы тяжести на вращающейся Земле. Уравнение движения тела имеет вид: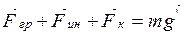 . (2.59)
. (2.59) , и заменив его более общим
, и заменив его более общим , (2.60)
, (2.60) . (2.61)
. (2.61)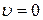 , т.е. для момента, когда тело начинает движение или падение из состояния покоя.
, т.е. для момента, когда тело начинает движение или падение из состояния покоя. тела можно выразить из формулы (2.59):
тела можно выразить из формулы (2.59):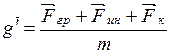 . (2.62)
. (2.62) , действующая на тело, движущееся относительно вращающейся Земли, есть величины неоднозначные, зависящие от скорости движения тела.
, действующая на тело, движущееся относительно вращающейся Земли, есть величины неоднозначные, зависящие от скорости движения тела.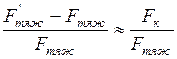 (2.63)
(2.63)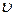 ≈ 67 м/с (≈ 240 км/ч) и
≈ 67 м/с (≈ 240 км/ч) и  (2.64)
(2.64) , (2.65)
, (2.65) – ускорение в начале свободного падения тела из состояния покоя, когда скорость движения еще очень мала
– ускорение в начале свободного падения тела из состояния покоя, когда скорость движения еще очень мала  .
.
 , действующая на тело, находящееся в воздухе
, действующая на тело, находящееся в воздухе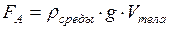 , (2.66)
, (2.66) (2.67)
(2.67)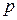 и его температуры Т;
и его температуры Т;  - молярная масса газа; R = 8,31 Дж/(моль × К) - универсальная газовая постоянная.
- молярная масса газа; R = 8,31 Дж/(моль × К) - универсальная газовая постоянная. является результирующей всех сил
является результирующей всех сил  , действующих на тело в областях фактического касания.
, действующих на тело в областях фактического касания. . (2.68)
. (2.68) , (2.69)
, (2.69) . (2.70)
. (2.70) в воздухе при температуре t = 200 С = 293 К и давлении ратм = 105 Па составляет
в воздухе при температуре t = 200 С = 293 К и давлении ратм = 105 Па составляет
 . (2.71)
. (2.71)


