
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип взвешивания без применения гирьСодержание книги
Поиск на нашем сайте
В зависимости от принципа действия одни приборы предназначены для измерения массы, другие – для измерения веса. И те и другие основаны на использовании гравитационного притяжения тел к Земле. Однако в одних случаях взвешивание производится с использованием мер массы, в других – безгирным способом. При взвешивании без применения гирь используются приборы, снабженные упругими весовыми элементами (пружинные, торсионные, крутильные весы и т.д.). Принцип взвешивания на таких весах основан на уравновешивании силы тяжести, действующей на тело, силой упругого сопротивления весового элемента. Чувствительным элементом пружинных весов является пружина, один конец которой подвешивается к опоре, а другой нагружают телами с известными массами и отмечают растяжение пружины, вызванное силой веса каждого тела (рис. 2.20). По закону Гука абсолютное удлинение пружины ∆l пропорционально весу тела Р: ∆l = αР. (2.72) где α – коэффициент пропорциональности. Поскольку вес тела равен силе тяжести (в отсутствии среды), то абсолютная деформация пружины пропорциональна произведению массы тела т на ускорение свободного падения g:
Рис. 2.20. Градуировка пружинных весов
Пружина обычно снабжается указателем, скользящим вдоль шкалы. При помощи пружинных весов измеряют не массу, а вес тела. Однако в большинстве случаев шкала пружинных весов градуируется при подвешивании тел с известной массой и, следовательно, проградуирована в единицах массы. Масса тела – величина постоянная, а значение ускорения свободного падения g зависит от географической широты и высоты над уровнем моря. В связи с этим изменяется вес тела и, следовательно, показания пружинных весов зависят от места их нахождения. Пружинные весы дают верные показания только в месте их градуировки. Кроме того, допускается, что после снятия нагрузки указатель возвращается в нулевое положение, т.е. в пружине под действием нагрузки не возникают остаточные деформации. Следует также учесть, что упругие свойства пружины зависят от температуры и изменяются со временем. Все это снижает точность пружинных весов. В результаты измерений массы с помощью пружинных весов необходимо вводить поправки, когда такая корректировка обоснована требованиями точности. Таким образом, определение массы тела безгирным методом требует учета множества факторов, влияющих на результат измерений, и сопряжено со значительно большими трудностями, чем измерение массы на рычажных весах. Плотность вещества
Распределение массы по объему тела можно характеризовать с помощью физической величины, называемой плотностью. Плотность численно равна массе вещества, содержащейся в единице объема тела. Если тело однородно, т.е. свойства его во всех точках одинаковы, то плотность его определяют по формуле
где m – масса; V – объем тела. Средняя плотность неоднородного вещества также равна отношению массы m тела к его объему V: r ср= Плотность в данной точке объема неоднородного вещества равна
В формуле (2.76) бесконечно малый объем нельзя понимать математически. Уменьшение Примечание. Флуктуация – случайное отклонение значения физической величины от ее среднего значения. Обозначив флуктуацию через ∆х, получим, что
Среднее арифметическое величины (2.77) равно нулю:
Поэтому в качестве характеристики флуктуаций берут среднюю квадратичную флуктуацию, равную
Относительная флуктуация величины х равна
В статистической физике доказывается, что относительная флуктуация аддитивной величины (т.е. такой величины, значение которой для тела равно сумме значений для отдельных его частей, например, массы) обратно пропорциональна корню квадратному из числа N молекул, образующих тело:
Плотность вещества, как правило, уменьшается с ростом температуры и увеличивается с повышением давления. При переходе вещества из одного агрегатного состояния в другое плотность изменяется скачкообразно - резко уменьшается при переходе в газообразное состояние и, как правило, увеличивается при кристаллизации. Плотность некоторых веществ (воды, чугуна и др.) аномально уменьшается при переходе из жидкой фазы в кристаллическую. За единицу плотности принимается плотность такого однородного вещества, единица объема которого содержит единицу массы вещества. В СИ единицей плотности является килограмм на кубический метр (кг/м3), в системе СГС – г/см3:
Примечание. В связи с введением в 1960 году Международной системы единиц (СИ) плотность воды при температуре 4°С и нормальном атмосферном давлении стала равной
Объем, занимаемый массой дистиллированной воды в 1 кг при температуре 40С, до 1964 г являлся единицей вместимости – литром. В СИ литр, следовательно, оказался равным
На XII Генеральной конференции по мерам и весам в 1964 г такое определение литра было отменено. Конференция постановила, что слово «литр» может использоваться лишь как специальное название, даваемое кубическому дециметру, и рекомендовала не использовать его для выражения результатов измерений объема высокой точности. СПИСОК ЛИТЕРАТУРЫ
1. Агапов, Б.Т. Лабоpатоpный пpактикум по физике / Б.Т. Агапов, Г.В.Максютин, П.И. Остpовеpхов [Текст]. М.: Высшая школа, 1982. С.68–70. 2. Воскресенский, П.И. Техника лабораторных работ / П.И. Воскресенский [Текст]. М.: Химия, 1973. С.231– 239. 3. Захаров, Л.Н. Начала техники лабораторных работ / Под ред. проф. Х.В. Бальяна [Текст]. Л.: Химия, 1981. С.65–72. 4. Ивеpонова, В.И. Физический пpактикум / В.И. Иверонова [Текст]. М.: ГИТТЛ, 1953. С.63–66. 5. Исакович, Е.Г. Весы и весовые дозаторы. Метрологическое обеспечение: Справочная книга метролога / Е.Г. Исакович [Текст]. М.: Изд-во стандартов, 1991. С. 3–10, 16–43. 6. Контрольно-измерительные приборы и инструменты / С.А. Зайцев, Д.Д. Грибанов, А.Н. Толстов, Р.В. Меркулов [Текст]. М.: Академия, 2003. С. 18–19. 7. Кортнев, А.В. Практикум по физике / А.В. Кортнев, Ю.В. Рублев, А.Н. Куценко [Текст]. М.: Высшая школа, 1961. С. 41– 43. 8. Мантуров, О.В. Толковый словарь математических терминов / О.В. Мантуров, Ю.К. Солнцев, Ю.И. Соркин, Н.Г. Федин / Под ред. проф. В.А. Диткина [Текст]. М.: Просвещение, 1965. С. 352–353. 9. Матвеев, А.Н. Механика и теория относительности / А.Н. Матвеев [Текст]. М.: Высшая школа,1976. С.391–399, 405–410. 10. Павленко, Ю.Г. Начала физики / Ю.Г. Павленко [Текст]. М.: Изд-во Моск. ун-та, 1988. С. 130–131. 11. Рудо, Н.М. Лабораторные весы и точное взвешивание / Н.М. Рудо [Текст]. М.: Стандартгиз, 1963. 152 с. 12. Савельев, И.В. Курс общей физики: в 3 т. Т.1: Механика. Молекулярная физика / И.В. Савельев [Текст]. М.: Наука, 1977. С.329–330. 13. Сивухин, Д.В. Общий курс физики: в 5 т. Т.1: Механика / Д.В. Сивухин [Текст]. М.: Наука, 1974. С. 68–71, 349–353. 14. Смирнова, Н.А. Единицы измерений массы и веса тела в Международной системе единиц / Н.А. Смирнова [Текст]. М.: Издательство комитета стандартов, мер и измерительных приборов при Совете Министров СССР, 1966. С.3–43. 15. Уродов, В.И. Практикум по физике / В.И. Уродов, В.С. Стрижнев [Текст]. Мн.: Выш. шк., 1973. С. 28–43. 16. Феоктистов, В.Г. Лабораторные весы / В.Г. Феоктистов [Текст]. М.: Изд-во Стандартов, 1979. 199 с. 17. Физическая энциклопедия: в 5 т. Т. 1. / Гл. ред. А.М. Прохоров [Текст]. М.: Советская энциклопедия, 1988. С. 262. 18. Физический энциклопедический словарь / Гл. ред. А.М. Прохоров [Текст]. М.: Советская энциклопедия, 1983. С. 70– 71, 73. 19. Чертов, А.Г. Международная система единиц измерений / А.Г. Чертов [Текст]. М.: Высшая школа, 1967. С. 161–162. 20. Щедровицкий, С.С. Техника измерений массы / С.С. Щедровицкий [Текст]. М.: Государственное издательство стандартов, 1961. 355 с. 21. Яворский, Б.М. Основы физики / Б.М. Яворский, А.А. Пинский [Текст]. М.: Наука, 1969. С. 93–101.
ЛАБОРАТОРНАЯ РАБОТА 3
С ПОМОЩЬЮ АНАЛИТИЧЕСКИХ ВЕСОВ
ЦЕЛИ РАБОТЫ
1. Изучение теоретических основ определения массы с помощью аналитических весов. 2. Рассмотрение влияния различных факторов на чувствительность весов. 3. Изучение методов точного взвешивания. 4. Изучение устройства аналитических весов АДВ-200 и правил взвешивания на аналитических весах. 5. Измерение массы тела с абсолютной погрешностью до десятых долей миллиграмма. ОСНОВНЫЕ ПОНЯТИЯ
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.146.94 (0.006 с.) |

 . (2.73)
. (2.73)
 , (2.74)
, (2.74) . (2.75)
. (2.75) . (2.76)
. (2.76) может продолжаться лишь до определенной величины, которая, с одной стороны, достаточно мала для того, чтобы свойства тела в пределах
может продолжаться лишь до определенной величины, которая, с одной стороны, достаточно мала для того, чтобы свойства тела в пределах  . (2.77)
. (2.77) . (2.78)
. (2.78) . (2.79)
. (2.79) . (2.80)
. (2.80)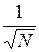 . (2.81)
. (2.81) , (2.82)
, (2.82)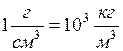 . (2.83)
. (2.83) .
. ;
; .
.


