
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы моделирования строительных конструкцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Сущность инженерного моделирования состоит в том, что натурный объект на основе теории подобия заменяется его аналогом-моделью. Различают физическое моделирование, когда исследование ведется на моделях, сохраняющих физическую природу изучаемого явления, и математическое - на моделях иной физической природы, имеющих такое же математическое описание (электрические, мембранные, гидравлические и другие аналоги). Моделирование дает возможность решить большое число довольно сложных задач: 1. Выявить экспериментальным путем при минимальных затратах Материала, трудоемкости и стоимости действительную картину распределения усилий во всех характерных сечениях и узловых сопряжениях элементов конструкций. 2. Произвести экспериментальным путем анализ напряженного состояния сложного сооружения взамен аналитического расчета, когда методы строительной механики и теории упругости не приемлемы. З. Проверить правильность гипотез, положенных в основу аналитического расчета. 5. Определить характер разрушения и разрушающую нагрузку. 6. Определить реальный запас прочности. 7. Установить влияние различных факторов на работу конструкции: свойств материалов, условий сопряжений, податливости основания и др. Для новых, сложных, малоизученных сооружений исследование может вестись в несколько этапов: 1) расчет на ЭВМ с применением математической или маломасштабной модели (1/10—1/20); 2) исследование крупномасштабной модели (1/2—1/5); 3) натурные испытания сооружения или его отдельных узлов и элементов. Теоретическая основа моделирования — теория подобия,. которая устанавливает определенные соотношения между геометрическими размерами, свойствами материалов, нагрузками и деформациями модели и натурной конструкции.. Различают простое и расширенное подобие. При простом (линейном) подобии масштабы всех безразмерных величин равны 1, при расширенном (нелинейном) они могут отличаться от 1, а разные величины одинаковой размерности могут иметь и отличные масштабы Подобными называют явления, происходящие в геометрически подобных системах, если отношения одноименных физических величин во всех сходственных точках представляют постоянные числа. При простом подобии безразмерные величины в сходственны точках равны:
где индекс «н» относится к натурному объекту, а «м» — к его модели: Переход от натурного объекта к модели осуществляется введением системы коэффициентов пропорциональности или масштабов преобразования:
где Е, Р, L, — соответственно модуль упругости, усилие геометрический размер и коэффициент Пуассона. Масштабы преобразования взаимосвязаны и не могут быть назначены произвольно. Так, при действии сосредоточенных. сил подобие напряженно-деформированного состояния обеспечивается, если удовлетворены условия
а при действии равномерно распределенной по длине нагрузки -
Выражения (6.1), (6.2), (6.3) называют индикаторами подобия. У подобных явлений индикаторы подобия равны единице. Это составляет содержание первой теоремы подобия. Вторая теорема устанавливает взаимосвязь преобразования физических уравнений в критериальные: если физические процессы подобны, их критерии подобия между собой равны. Третья тёорема устанавливает необходимые и достаточные условия подобия: для подобных явлений достаточно, чтобы они описывались одинаковыми уравнениями и имели подобные начальные и граничные условия. Условия подобия определяют путем анализа уравнений задачи или анализа размерностей входящих в уравнения величин. Размерность величин записывается символически с помощью букв, присвоенных основным физическим величинам. Так, если М—масса, Т—время, а L—длина, то размерность напряжения Величины могут быть и безразмерными, например относительная деформация ε, коэффициент Пуассона. Необходимые условия простого подобия: 1. Модель и натурный объект геометрически подобны. 2. Коэффициенты Пуассона для материалов модели и натуры должны быть равными. 3. Относительные деформации модели и натуры равны. 4. Все нагрузки, действующие на модель, находятся в таком же отношении, как и нагрузки, действующие на натурный объект. 5. Материалы модели и натуры могут отличаться при соответствующем коэффициенте масштаба напряжений. Рассмотрим пример моделирования изгибаемого элемента. Дана балка (рис. 6.12, а), изготовленная из бетона и загружена в середине пролета сосредоточенной силой Р=6 кН. (Размеры балки указаны в сантиметрах.) При модуле упругости материала натуры Ен=2,4·104МПа напряжение, относительное удлинение нижнего волокна и прогиб в середине пролета балки соответственно равны:
Рис. 6.12. Бетонная балка: а - натурная конструкция; б - модель
Модель (рис. 6.12, 6) изготовлена из бетона той же прочности ( Еr= 1и
Масштабы силового и геометрического подобия в данном случае не совпадают. Оригинал в модель отличаются размерами, свойствами материалов и соотношениями нагрузки. Для оценки точности и достоверности результатов модельных испытаний при переходе от модели к реальной конструкции должна учитываться изменчивость свойств оригинала и модели и даваться оценка погрешности полученных результатов. Под планированием эксперимента понимается выбор числа моделей и образцов для определения их свойств при заданной вероятности Р и принятой погрешности
где При моделировании железобетонных конструкций, учитывается масштабный фактор как функция случайного аргумента призменной прочности бетона. Это вызвано тем, что при изготовлении образцов из одного и того же материала с уменьшением размеров практически не всегда удается точно найти математическое ожидание При испытаниях больших и малых призм выявляется действие масштабного фактор а, учитывающего некоторые различия натурного и модельного материалов. Выбор материала для изготовления модели и методики исследования напряженно-деформированного состояния является важным вопросом теории и практики моделирования строительных конструкций. Крупномасштабные модели обычно изготавливаются из тех же материалов, что и натурная конструкция: сталь, алюминий, железобетон, армоцемент, древесина, пластмассы. В зависимости от цели исследования модуль упругости материала модели можёт отличаться от модуля упругости материала натуры или быть идентичным. Маломасштабные модели, как правило, работают в упругой стадии. Поэтому их следует изготавливать из материалов с хорошими упругими свойствами. К таким материалам относятся металлы, оргстекло, некоторые пластмассы и минеральные материалы Если предусматривается исследование работы модели в упругопластической стадии, материал должен обладать низким модулем упругости и высокой пластичностью при обязательном выполнении заданных соотношений между напряжениями и деформациями. Выбор масштаба и материала модели зависит от целей и задач моделирования, вида исследуемой конструкции, способа изготовления и загружения, методики исследования напряженно-деформированного состояния, производственных возможностей и технико-экономических соображений Так, если для исследования напряженно-деформированного состояния выбран поляризационно-оптический метод, для изготовления
6.13. Испытание моделей, изготовленных: а —из железобетона; б —клееной древесины; в — металла
моделей применяются материалы: стекло, целлулоид, фенолформальдегидные смолы, полиэфирные смолы, плексиглас, полиметилметакрилат, полибензилметакрилат, глифтамал, полидиаллилфталаты, сшитый полихлорстирол, оптически чувствительные гели, полиуретановые каучуки, прозрачные поликристаллы галлоидов серебра и таллия и др. Материалы для изготовления моделей должны отличаться постоянством физико-механических свойств, хорошо обрабатываться, склеиваться или свариваться. Наиболее часто применяются следующие методы исследования напряженно-деформированного состояния моделей: тензометрический, поляризационно-оптический, фотоупругих в хрупких покрытий, делительных сеток и муаровык полос, голографии и физической аналогии. Сущность тензометрического метода заключается в том, что в заданных участках модели устанавливают тензометры или наклеивают тензорезисторы для замера фибровых деформаций с последующим вычислением напряжений. Поляризацяонно-оптический метод основан на изменении оптических свойств определенных пьезооптических материалов, которые под действием напряжений приобретают свойство двойного лучепреломления. Для этого через модель пропускают поляризованный пучок света (рис. 6.14) и рассматривают на. экране интерференционную картину в виде системы светлых и черных полос (рис. 6.15), характеризующих напряженное состояние модели. По картине полос одинаковой окраски в заданных точках модели устанавливают разность главных напряжений
Рис. 6.14. Схема поляризационно-оптической установки: 1- Источник света; 2- поляризатор; 3- модель; 4- анализатор; 5- экран
Рис. 6.15. Интерференционная картина при испытании балки на двух опорах сосредоточенной силой
Для полного представления о напряженном состоянии требуется также определить каждое из главных напряжений. Определение напряжений обычно выполняется одним из трех методов: экспериментальным; численным или смешанным. Экспериментальные методы применяют: для определения с помощью оптиметров или тензометров приращения толщины модели Относительная деформация
откуда
Для повышения точности измерений широко применяют интерферометрические методы получения изопахик - линий, равных сумме главных напряжений Измерение толщин моделей при этом производится оптическим квантовым генератором — лазером. Численные методы разделения напряжений основаны на применении уравнений механики сплошной среды. В смешанных методах численный анализ дополняют данными экспериментов. Исследование решений линейных упругих задач на моделях, изготовленных из оптически чувствительных и механически изотропных материалов, называют методом фотоупругости. Упругопластические задачи решают методом фотопластичности. Материалы, проявляющие при загружении свойства ползучести, изучают методом фотоползучести. для исследования больших деформаций применяют упругие изотропные материалы — полиуретановые каучуки (прозрачные резины). Однако возможности исследователя при испытаниях моделей строительных конструкций, изготовленных из оптически прозрачных материалов, весьма ограниченью. Поэтому получили развитие другие, более удобные для применения, методы. Метод фотоупругих покрытий заключается в том, что на поверхность модели, изготовленной из любого материала, в том числе и материала натурной конструкции, наносится тонкий слой покрытия, работающий в процессе испытания модели упруго. При загружении модели в покрытии возникает пьезооптический эффект, с помощью которого изучают характер распределения деформаций на поверхности модели. Покрытие может наноситься не на всю модель, а только на отдельные участки. В наиболее характерных сечениях модели могут применяться вклейки из материала с высокой оптической чувствительностью. Модель может изготовляться и из двух материалов с разной оптической чувствительностью или из одного с разделением отдельных частей модели полупрозрачными, зеркально отражающими слоями или поляроидной пленкой. Разработаны методы, позволяющие измерять оптические эффекты в отдельных слоях модели с помощью «замораживания» и последующей разрезкой модели на отдельные слои для изучения в полярископе. Под «замораживанием» понимают способность некоторых полимеров сохранять неизменной оптическую анизотропию, возникающую при загружении модели при определенной температуре или в состоянии частичной полимеризации. Если загрузить модель, которая в результате воздействия повышенной температуры или неполной полимеризации находится в высокоэластическом состоянии, а затем охладить ее или произвести полимеризацию, то после снятия нагрузки оптические эффекты остаются неизменными, как бы замораживаются. Представляют интерес простые методы качественной оценки распределения деформаций на первом этапе исследования модели с тем, чтобы принять для последующих испытаний наиболее обоснованную методику изучения напряженно-деформированного состояния и схему установки измерительных приборов. К числу таких методов можно отнести метод хрупких покрытий. Метод хрупких покрытий характеризуется тем, что на поверхность модели наносится тонкое лаковое покрытие. Состав лака подбирается так, чтобы разрыв пленки происходил в пределах упругих деформаций материала модели. При загружении модели в наиболее напряженных сечениях в покрытии возникают трещины, направленные перпендикулярно к оси максимальных удлинений. По характеру расположения трещин и величине нагрузки, при которой они возникают, можно судить о напряженно-деформированном состоянии модели. По картине трещинообразования можно сделать вывод о требуемой схеме расположения тензорезисторов для более точной количественной оценки возникающих напряжений. Для исследования больших пластических деформаций и ползучести применяют метод делительных сеток. На поверхность модели наносят делительную сетку, форму и положение которой сравнительно просто оценивают в какой-либо системе координат. При загружении модели сетка деформируется, и определяют приращения деформаций. В методе муаровых полос используются специальные сетки— растры. Одна из сеток наносится на поверхность модели, вторая — на эталон. Совмещая оптическим способом рабочую сетку с эталонной, получают муаровые полосы, характеризующие напряженно-деформированное состояние модели. Перенос растрового изображения с эталона на модель производится фотографическим способом. Для более совершенной фиксации отпической информации используется метод голографии. Из теории упругости известно, что сумма главных напряженней
для решения данного уравнения при испытаниях моделей пользуются электрогидродинамической аналогией, основанной на том, что при плоском напряженном состоянии функция суммы ЛЕКЦИЯ 7. ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ДЛЯ СТАТИЧЕСКИХ ИСПЫТАНИЙ КОНСТРУКЦИЙ.
Назначение и виды приборов.
Основная задача статических испытаний строительных конструкций — выявление их напряженно-деформированного состояния под нагрузкой, оценка несущей способности, жесткости и трещиностойкости конструкций. Растяжение, сжатие, изгиб, кручение, срез в конструкциях сопровождаются линейными деформациями, прогибами, изменениями углов поворота и сдвигами. Измерение перечисленных деформаций производится специальными приборами как с непосредственным снятием отсчетов по шкалам (показывающие приборы), так и с помощью измерительных преобразователей, работающих дистанционно [3.2,3.11,3.14,3.15]. Большие линейные деформации и перемещения, а также прогибы измеряют прогпбомерамп и индикаторами часового типа. Углы поворота измеряют клинометрами, смещение параллельных волокон при сдвиге — сдвигомерами. Измерение фибровых деформаций производят тензометрами и тензорезисторами. По деформациям определяют напряжения, использования при упругой работе материала закон Гука, а при пластической — инвариантные величины интенсивности касательных и нормальных напряжении. При испытаниях строительных конструкций, кроме перечисленных, применяют и другие приборы: микроскопы, щупы, щелемеры, ультразвуковую аппаратуру, геодезические, приборы и инструменты и т. д.
|
||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 1370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.014 с.) |

 ;
; 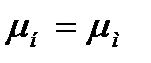 ;
;  ;
;  ,
, — нормальное напряжение; и — приращение длины х.
— нормальное напряжение; и — приращение длины х.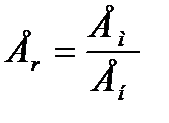 ;
;  ;
;  ;
;  ,
,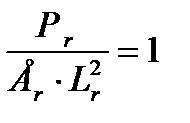 ; (6.1)
; (6.1) , (6.2)
, (6.2)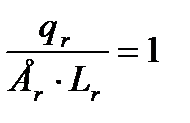 (6.3)
(6.3)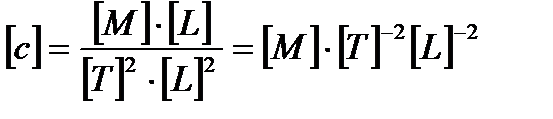 , а изгибающего момента [М] [Т]-2[L]-2
, а изгибающего момента [М] [Т]-2[L]-2 ;
;  ;
; 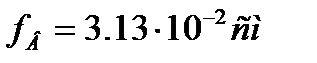 .
.
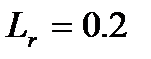 . Масштаб нагрузки определяем по формуле (6.1): Рr= 0,04. Линейные размеры модели уменьшены в 5 раз, а нагрузка - в 25 раз. Напряжения, относительные удлинения и прогибы оригинала после испытания модели определяются по следующим формулам:
. Масштаб нагрузки определяем по формуле (6.1): Рr= 0,04. Линейные размеры модели уменьшены в 5 раз, а нагрузка - в 25 раз. Напряжения, относительные удлинения и прогибы оригинала после испытания модели определяются по следующим формулам: ;
;  ;
; 
 . для множителя преобразования
. для множителя преобразования 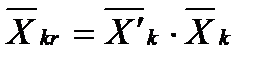 предложена интервальная оценка, где
предложена интервальная оценка, где  и
и  —усредненные величины, полученные по результатам испытаний оригинала и модели:
—усредненные величины, полученные по результатам испытаний оригинала и модели:
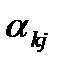 — показатель степени, с которой множитель преобразования входит в индикатор подобия;
— показатель степени, с которой множитель преобразования входит в индикатор подобия; 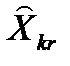 ,. — математическое ожидание множителя преобразования.
,. — математическое ожидание множителя преобразования. материала модели, поэтому обычно
материала модели, поэтому обычно  определяется некорректно.
определяется некорректно.


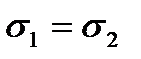 , называемую ценой деления полосы модели. Порядок чередования волос определяют подсчетом числа затемнений при увеличении нагрузки на модель. По напряжению модели
, называемую ценой деления полосы модели. Порядок чередования волос определяют подсчетом числа затемнений при увеличении нагрузки на модель. По напряжению модели  определяют напряжение в натурной конструкции
определяют напряжение в натурной конструкции  .
.

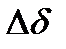 при загружении.
при загружении. ,
, .
. в плоскости модели при отсутствии объемных сил удовлетворяет уравнению Лапласа
в плоскости модели при отсутствии объемных сил удовлетворяет уравнению Лапласа ,
, — оператор Лапласа.
— оператор Лапласа.


