
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение. Погрешности измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Введение
Лабораторный практикум содержит описание лабораторных работ, подготовленных в соответствии с рабочей программой, утвержденной для медицинских ВУЗов. Изложению работ предшествует вводное занятие, посвященное вычислению погрешностей, построению графиков и методике выполнения простейших измерений. Для облегчения усвоения учебного материала, в практикуме к каждой лабораторной работе изложен теоретический материал в соответствии с программой курса физики для медицинских ВУЗов. Все представленные работы составлены по единому плану и содержат элементы теории и описание установки. Кроме того, приводится порядок выполнения работы, последовательность обработки результатов экспериментальных измерений и вычислений. Практикум позволит изучить основные законы физики, физические явления, а также закономерности, лежащие в основе процессов, протекающих в человеческом организме. Он даст возможность расширения и углубления знаний, умений и навыков для дальнейшего продолжения обучения и успешной профессиональной деятельности. Одновременно с этим он познакомит обучающихся с правилами техники безопасности в физических лабораториях, физическими основами устройств и функционирования медицинской аппаратуры. Практикум научит пользоваться физическим оборудованием и измерительной техникой, производить эксперимент и расчеты по его результатам. Подготовленный практикум поможет студентам лечебного факультета в овладении общекультурными и профессиональными компетенциями. В частности, следующими общекультурными компетенциями: – способности и готовности анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1); – способностью и готовностью к логическому и аргументированному анализу, к публичной речи, ведению дискуссий и полемике, к редактированию текстов профессионального содержания, к осуществлению воспитательной и педагогической деятельности, к сотрудничеству и разрешению конфликтов, к толерантности (ОК-5); а также следующими профессиональными компетенциями: – способностью и готовностью выявлять естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, использовать для их решения соответствующих физико-химический и математический аппарат (ПК-2); – способностью и готовностью к формированию системного подхода к анализу медицинской информации, опираясь на всеобъемлющие принципы доказательной медицины, основанной на поиске решений с использованием теоретических знаний и практических умений в целях совершенствования профессиональной деятельности (ПК-3); – способностью и готовностью к работе с медико-технической аппаратурой, используемой в работе с пациентами, владеть компьютерной техникой, получать информацию из различных источников, работать с информацией в глобальных компьютерных сетях, применять возможности современных информационных технологий, для решения профессиональных задач (ПК-9); – способностью, готовностью выполнять основные лечебные мероприятия при наиболее часто встречающихся заболеваниях и состояниях у взрослого населения и подростков, способных вызвать тяжелые осложнения и (или) летальный исход: заболевания нервной, эндокринной, иммунной, сердечно-сосудистой, дыхательной, пищеварительной, мочеполовой систем и крови, своевременно выявлять жизнеопасные нарушения (острая кровопотеря, нарушение дыхания, остановка сердца, кома, шок), использовать методики их немедленного устранения, осуществлять противошоковые мероприятия (ПК-19); – способность и готовность давать рекомендации по выбору оптимального режима двигательной активности в зависимости от морфофункционального статуса, определять показания и противопоказания к назначению средств лечебной физкультуры, физиотерапии, рефлексотерапии, фитотерапии, гомеопатии и других средств немедикаментозной терапии, использовать основные курортные факторы при лечении взрослого населения и подростков (ПК-24); – способностью и готовностью использовать нормативную документацию, принятую в здравоохранении (законы Российской Федерации, технические регламенты, международные и национальные стандарты, приказы, рекомендации, терминологию, международные системы единиц (СИ), действующие международные классификации), а также документацию для оценки качества и эффективности работы медицинских организаций (ПК-27); – способностью и готовностью изучать научно-медицинскую информацию, отечественный и зарубежный опыт по тематике исследования (ПК-31); – способностью и готовностью к участию в освоении современных теоретических и экспериментальных методов исследования, с целью создания новых перспективных средств, в организации работ по практическому использованию и внедрению результатов исследований (ПК-32). Диагностика формирования компетенций обучающихся в процессе изучения учебных дисциплин, междисциплинарных курсов или иных учебных модулей осуществляется посредством проведения текущего, предварительного, рубежного или итогового контроля – контролирующих мероприятий. Последовательность проведения контролирующих мероприятий заключается в планировании, организации и проведении с последующей оценкой результатов контроля как процедуры сопоставления зафиксированных ответов обучающихся с требованиями к решению учебных задач. Проведение контроля предполагает использование контрольных измерительных материалов в соответствии с императивными, дозволительными и рекомендательными нормами, определенными технологией проведения контролирующих мероприятий. Существует несколько методов оценки профессиональных качеств экспертов, которые делят на априорные, апостериорные и тестовые. К априорным методам относят самооценивание, взаимное оценивание и документационный метод. Методы самооценки основаны на использовании балльных, вербально-числовых и вербальных шкал. Апостериорные методы оценки качества экспертов основаны на сравнении отклонений индивидуальных данных от результирующей групповой оценки. С помощью апостериорных методов можно оценить коньюктурность, конформизм и воспроизводимость оценок эксперта. Тестовые методы оценки экспертов основаны на тестировании с целью установления квалификации, навыков и опыта работы эксперта. Оценка качества подготовки студентов будет включать текущий контроль, рубежный контроль и итоговый контроль. Текущий контроль, то есть проверка усвоения учебного материала, регулярно осуществляемая на протяжении семестра, осуществляется в форме устных опросов во время практических занятий. Рубежный контроль осуществляется в виде сдачи коллоквиума. Полученные в результате этого данные служат основой для балльно-рейтинговой оценки успеваемости студента. Итоговый контроль проводится в конце семестра в форме зачета и завершает изучение дисциплины служит для проверки результатов обучения в целом, при этом оценивается совокупность приобретенных студентом общеобразовательных и профессиональных компетенций. Настоящий практикум является первой частью запланированного издания с общим объемом 18–20 лабораторных работ, с учетом ФГОС третьего поколения. Практическое занятие Равноточных измерений Измерения называются равноточными, если они проведены одинаковыми по точности методами, или одним и тем же методом в одинаковых условиях. В результате n измерений некоторой физической величины x, истинное значение которой X0 = mx (если нет систематических погрешностей) неизвестно, из-за наличия случайных погрешностей получается ряд численных значений x1; x2, …, xn, которые в общем случае отличаются друг от друга и от X0. При обработке результатов этих измерений возникают две задачи: 1. Нахождение по результатам отдельных измерений наилучшей оценки истинного значения, т.е. значения, наиболее близкого к истинному; 2. Определение погрешности полученной оценки. Для большого числа практических случаев, когда грубые погрешности (промахи) встречаются редко, а случайные погрешности распределены по нормальному закону, наилучшей оценкой измеряемой величины является среднее арифметическое
Отдельные результаты измерений являются случайными величинами, поскольку содержат случайные погрешности ∆Хi: ∆хi = хi - х0. Среднее арифметическое
также будет случайной. Это говорит о том, что истинное значение абсолютной погрешности найти невозможно, можно лишь тем или иным способом приближенно оценить ее значение. Например, можно считать, что с определенной вероятностью значение абсолютной погрешности по абсолютной величине будет меньше некоторой заданной величины
Отсюда следует, что истинное значение измеряемой величины с вероятностью
Интервал Таким образом, для характеристики случайной погрешности необходимо знать два числа, а именно – величину оценки абсолютной погрешности В качестве ширины доверительного интервала можно взять
Среднее арифметическое имеет меньшее рассеивание и соответственно его среднеквадратичная погрешность будет меньше в
В физических, биологических, медицинских, физиологических и др. измерениях обычно пользуются значениями доверительной вероятности
где Если взять величину абсолютной погрешности Наряду со среднеквадратичной погрешностью
Все приведенные выше результаты теории случайных погрешностей применимы для характеристики точности измерения лишь в случае, если измерение многократно повторено. Последовательность действий при оценке истинного значения измеряемой величины и оценки случайной погрешности следующая: 1. находится среднее арифметическое по результатам измерений:
2. находится среднеквадратическая погрешность отдельного результата измерения:
3. находится максимальная абсолютная погрешность отдельного измерения:
4. проверяется, все ли результаты измерений укладываются в интервал 5. находится среднеквадратическая погрешность среднего арифметического:
6. находится из таблицы коэффициент
7. записывается результат измерения:
при заданном 8. если необходимо, то находится относительная погрешность, при этом, поскольку Х0 неизвестно, приближенно его заменяют на
Измерений Чаще всего интересующая нас величина Х непосредственно не измеряется. Вместо этого измеряются некоторые величины
Для каждой из величин Т.к. каждая из величин
Погрешность результата косвенных измерений зависит от погрешностей прямых измерений каждой из величин, входящих в эту формулу. Для расчета абсолютной погрешности косвенного измерения при заданной доверительной вероятности
где Для нахождения максимальной абсолютной погрешности используют формулу:
Окончательный результат измерений и вычислений записывается в виде при заданной доверительной вероятности или При этом обязательно указывать название характеризующей результат меры точности
Порядок обработки результатов косвенных измерений следующий: 1. находятся средние арифметические 2. находится среднее значение результата косвенных измерений по формуле (23). 3. находится абсолютная погрешность косвенного измерения по формуле (24). 4. записывается результат измерения: Величины нагрузки P
11. На основании графика можно найти абсолютную погрешность в определении одной из величин, если известна абсолютная погрешность другой величины. Пусть график изображает зависимость y = f(x) и известно, что некоторое значение величины Х измерено с погрешностью Δх (точка Х0). Тогда на графике откладывают на соответствующей оси около значения Х0 величину ΔX в выбранном масштабе и по графику находит соответствующую ей величину отрезка ΔY (см. рис.2). Найденное ΔY и будет представлять собой абсолютную погрешность в определении Y.
Задачи для самостоятельного решения 1. Постоянная термопары определяется по формуле
где Rr – сопротивление гальванометра 30 Ом, I – ток термопары (показания гальванометра) T2 - T1 – разность температур теплого и холодного слоев термопары: T1 - T2 = 10 К. По показаниям гальванометра оцените среднее значение и погрешность измерения ˚ С при γ = 0,95 I · 10-10 А: 23; 24; 23,5; 25; 24,2.
2. Коэффициент вязкости жидкости определяется формулой (капиллярный вискозиметр): где t2 – время истечения из капилляра исследуемой жидкости объемом V; t1 - время истечения из капилляра дистиллированной воды объемом V; Обработать данные при
t1 = 9,8 10 10,2 9,9 9,9 t2 = 38,8 40,2 40 40,3 40,5
3. Определить размеры коллоидной частицы по скорости ее оседания в монодисперсной среде из формулы Стокса (
где
g - ускорение силы тяжести (9,8 м/сек2).
Скорость оседания в пяти измерениях составила:
4. Вес тела при взвешивании по методу Гаусса определяется по формуле где: P1 – вес тела на левой стороне весов [г], P2 – вес тела на правой стороне весов [г].
В результате взвешивания получены результаты: P1 = 2,32 г, 2,21 г, 2,25 г, 2,24 г, 2,23 г. P 2 = 2,41 г, 2,39 г, 3,4 г, 2,41 г, 2,42 г. Найти
5. При определении к.п.н. методом отрыва капель формула для его подсчета имеет вид: Где:
Лабораторная работа №1 Краткая теория Простейшим случаем вращательного движения является вращение твердого тела вокруг неподвижной оси. При этом все точки тела описывают окружности, центры которых лежат на одной прямой, являющейся осью вращения. Вращательное движение удобно характеризовать углом поворота «j», угловой скоростью « Аналогом величин, характеризующих поступательное движение во вращательном движении вокруг неподвижной оси являются: 1) пройденный путь S - угол поворота j; 2) линейная скорость u = dS/dt - угловая скорость 3) ускорение 4) масса тела m - момент инерции J вращающейся материальной точки массой m относительно оси неподвижной оси на расстоянии r: J = mr2 , а для любого тела – 5) сила 6) импульс тела Выполнение работы 1. Грузы m1 на маятнике Обербека (крестовине) закреплены на некотором одинаковом расстоянии R от оси вращения (рис.4). 2. Измерить расстояние R от оси вращения до центра масс груза m1. 3. Намотать нить на шкив крестовины и последнюю придерживать рукой. 4. Подвесить к нити груз массой m (100, 200 или 300 гр) и совместить нижнюю часть груза с верхней меткой на стене. 5. Дать возможность грузу массой m опускаться. Измерить время движения t груза на расстоянии h = 0,5 м от верхней до нижней меток на стене. 6. Результаты измерений занести в таблицу 1. 7. Измерения провести при двух различных грузах массой m по 3 раза с каждым при h=const. 8. По формулам 11, 12, 13 (см. ниже) по средним значениям «t» вычислить линейное ускорение «a», угловое ускорение «e», вращающий момент «M», действующий на маятник
где r – радиус шкива, на который наматывается нить.
9. По формуле «14» высчитать момент инерции, найденный практически Jпракт = М / e (14)
10. Вычислить теоретически момент инерции «Jтеорет» по формуле (15) и сравнить с результатом Jпракт, полученным в пункте 9 (формула 14).
Сравнивая Jпракт = М/e, найденный из основного уравнения динамики вращательного движения (e= M/J), с его теоретическим значением
11. Вычислить абсолютную по формуле (16) и относительную по формуле (17) погрешность измерений для одной из серий результатов. Вычисление погрешностей 1) Абсолютная погрешность измерения практического значения момента инерции маятника Обербека:
где 2) Относительная погрешность измерения практического значения момента инерции маятника Обербека:
Таблица 1 Результаты измерений и вычислений
m1=154 г = 0,154 кг – масса каждого груза на стержне, m2 =184 г=0,184 кг – масса каждого из 2-х стержней, l =52 cм=0,52 м – длина стержня, r =1 см=0,01м – радиус шкива, g =9,8 м/с2, h =0,5 м, Dh =1см=0,01м
Рисунок 4. Маятник Обербека
Контрольные вопросы 1. Перечислите величины, характеризующие кинематику вращательного движения, момент инерции и единицы его измерения. 2. Момент инерции различных тел (с выводом формул для стержня, тонкого кольца, тонкой сферы и др.). 3. Момент силы (векторная форма записи), направление и единицы его измерения. 4. Основное уравнение динамики вращательного движения. 5. Закон сохранения момента количества движения (привести примеры использования его на практике). 6. Сочленения и рычаги в опорно-двигательном аппарате человека. 7. Центрифугирование.
Лабораторная работа №2 Краткая теория Теплоемкость газов При термодинамическом равновесии состояние газа в целом может характеризоваться тремя параметрами: давлением P, объемом V и температурой Т. Соотношение, связывающее между собой эти величины, называется уравнением состояния газа. Для идеального газа таковым является уравнение Клапейрона - Менделеева, которое для данной массы газа m имеет вид:
где m - молярная масса газа, R- универсальная газовая постоянная. При равновесном переходе газа из одного состояния в другое, т.е. при термодинамическом процессе, должно выполниться первое начало термодинамики, которое можно сформулировать следующим образом: количество теплоты dQ, переданное газу, идет на изменение его внутренней энергии dU и на работу dA, совершаемую газом против внешних сил: dQ = dU + dA Элементарная работа dA=pdV, а внутренняя энергия одного киломоля идеального газа определяется по формуле
где i - число степеней свободы молекулы газа, Для одноатомных молекул i =3 (только 3 поступательных степени свободы); для двухатомных i =5 (3 поступательных и 2 вращательных); для трех и более атомных i =6 (3 поступательных и 3 вращательных). Теплоёмкостью С называется величина, равная отношению сообщенного телу при нагревании количества теплоты dQ к вызванному этим процессом изменению температуры dT:
Различают удельную теплоемкость Cуд – теплоёмкость одного килограмма газа в молярную Сm - теплоёмкость одного киломоля газа. Эти теплоёмкости связаны между собой равенством:
Теплоемкости для одного и того же газа не являются постоянными величинами, а зависят от характера процесса, при котором происходит нагревание газа, т.к. одному и тому же изменению температуры dT могут соответствовать различные значения работы dA. Рассмотрим основные изопроцессы, протекающие в одном киломоле идеального газа и найдем соответствующие им теплоёмкости. а) Изохорический процесс (V = const) В этом случае dV=0, следовательно dA=0, и всё подводимое к газу количество теплоты идет на увеличение его внутренней энергии dU: dQ = dU. Тогда молярная теплоемкость при постоянном объёме, учитывая (I), равна:
б) Изобарический процесс (p = const) В этом случае молярная теплоемкость
Из уравнения состояния газа для одного киломоля имеем:
Т.к, p = const,то dp =0 и pdV=RdT. (4а) Подставляя (4а) в (3) и заменяя dU согласно (2) на
в) Изотермический процесс (T = const) В этом случае dT =0 и dQ = dA,т.е. все подводимое количество теплоты идет на совершение газом работы, а его внутренняя энергия остается постоянной. Т.к. температура при этом не изменяется, то молярная теплоёмкость равна Элементарная работа при изотермическом процессе определяется уравнением
Полная работа
где V1 и V2 - начальный и конечный объем газа при изотермическом расширении Из уравнения Клапейрона- Менделеева для любой массы газа
Находим давление Тогда Данный интеграл имеет следующее решение
Итак, работа газа при изотермическом расширении определяется уравнением
г) Адиабатический процесс (dQ = 0, dU + dA = 0) – процесс, происходящий при отсутствии теплообмена между газом и окружающей средой. Т.к. при этом dQ =0,то молярная теплоёмкость равна нулю. Выведем уравнение адиабатического процесса (уравнение Пуассона). dA = -dU или pdV = -CvdT. (6)
Разделив равенство (4) на (6), учитывая (5),получим:
где Если вместо Ср и Сv подставить в выражение для g их значения через число степеней свободы идеального газа i, то получим:
Интегрируя и потенцируя уравнение (7), получим уравнение Пуассона:
В данной работе определяется отношение g для воздуха по скорости звука в нем. Теория метода Звуковые волны в газах являются продольными и представляют собой последовательные сжатия и разрежения частиц газа. Скорость распространения звуковой волны зависит от упругости газа и его плотности:
где Е – модуль упругости (Юнга). Модуль упругости Е, по определению, есть коэффициент пропорциональности между относительным удлинением тела
В продольной волне при одностороннем растяжении относительное удлинение
При распространении волн в газовой среде вследствие сжатий и разрежений происходит изменение температуры различных учас
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.036 с.) |

 отдельных результатов измерения:
отдельных результатов измерения: . (7)
. (7)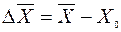 (8)
(8)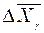 , т.е.
, т.е. . (9)
. (9)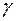 накрывается интервалом
накрывается интервалом 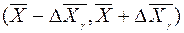 , т.е.
, т.е. 
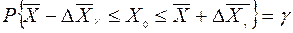 . (10)
. (10)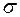 - среднеквадратичную погрешность. Для отдельного измерения она равна:
- среднеквадратичную погрешность. Для отдельного измерения она равна: . (11)
. (11)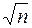 раз.
раз.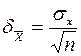 . (12)
. (12)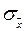 , т.е.:
, т.е.: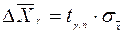 , (13)
, (13) - коэффициент, зависящий от величины доверительный вероятности
- коэффициент, зависящий от величины доверительный вероятности 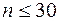
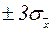 , то вероятность того, что доверительный интервал
, то вероятность того, что доверительный интервал 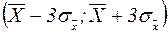 содержит Х0 будет равна
содержит Х0 будет равна 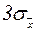 невозможно. Это правило известно под названием “правила трех сигм”.
невозможно. Это правило известно под названием “правила трех сигм”.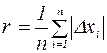 . (14)
. (14) , (15)
, (15) , (16)
, (16) , (17)
, (17) , если да, то переходим к следующему пункту, если нет, то такое значение отбрасыватся (тем самым мы избавляемся от промахов) и вычисления следует начать сначала.
, если да, то переходим к следующему пункту, если нет, то такое значение отбрасыватся (тем самым мы избавляемся от промахов) и вычисления следует начать сначала. (18)
(18)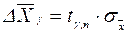 (19)
(19) (20)
(20)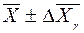 накрывает
накрывает 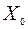 , т.е.
, т.е. 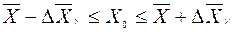 .
. . (21)
. (21)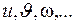 ,а затем вычисляется искомая величина Х, которая является функцией указанных непосредственно измеренных величин:
,а затем вычисляется искомая величина Х, которая является функцией указанных непосредственно измеренных величин: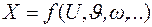 (22)
(22)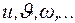 мы находим, как было указано выше, наиболее вероятное значение, т.е. среднеарифметическое из измеренных значений
мы находим, как было указано выше, наиболее вероятное значение, т.е. среднеарифметическое из измеренных значений 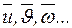 ; и оцениваем их погрешности – либо вычисляем их среднеквадратичные погрешности
; и оцениваем их погрешности – либо вычисляем их среднеквадратичные погрешности 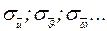 для случая многократных изменений, либо находим максимальные погрешности
для случая многократных изменений, либо находим максимальные погрешности  , в случае отсутствия разброса в значениях
, в случае отсутствия разброса в значениях  при многократных измерениях.
при многократных измерениях.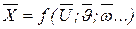 . (23)
. (23) (24)
(24) - погрешности прямых измерений при заданной доверительной вероятности
- погрешности прямых измерений при заданной доверительной вероятности 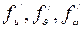 - частные производные функции
- частные производные функции 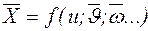 по переменным
по переменным  по одной из них, например, по u, является обычной производной функции f по u, только при этом другие переменные
по одной из них, например, по u, является обычной производной функции f по u, только при этом другие переменные 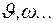
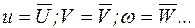
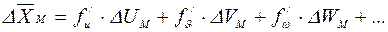 (25)
(25)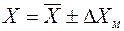 , где
, где 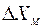 - максимальная абсолютная погрешность.
- максимальная абсолютная погрешность.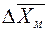 ). Если необходимо, указывается и значение относительной погрешности
). Если необходимо, указывается и значение относительной погрешности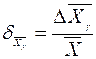 или
или 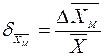 (26)
(26) и абсолютные погрешности
и абсолютные погрешности  , а объем выборки может быть для них различным.
, а объем выборки может быть для них различным. 10. Кривую, построенную по экспериментально полученным точкам для некоторой области изменения аргумента, можно затем использовать для нахождения значений функции для любого промежуточного значения аргумента на этой области. Эта операция называется графическим интегрированием. Например, по графику (рис. 1) можно найти значение чувствительности весов αх при нагрузке Рх = 75 г: α 75 =
10. Кривую, построенную по экспериментально полученным точкам для некоторой области изменения аргумента, можно затем использовать для нахождения значений функции для любого промежуточного значения аргумента на этой области. Эта операция называется графическим интегрированием. Например, по графику (рис. 1) можно найти значение чувствительности весов αх при нагрузке Рх = 75 г: α 75 = 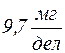 .
. ,
, ,
, и известных
и известных (вода)
(вода) (кровь)
(кровь)

 )
)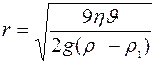 ,
, - коэффициент вязкости среды (4 сПз),
- коэффициент вязкости среды (4 сПз),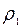 - плотность среды (0,95 г/см3),
- плотность среды (0,95 г/см3),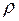 - плотность частицы (3 г/см3),
- плотность частицы (3 г/см3),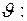 8,1 8,25 8,3 8,2 8,15 мм/час.
8,1 8,25 8,3 8,2 8,15 мм/час.
 и
и 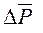 , при
, при 

 - плотность эталонной жидкости (1 г/см3),
- плотность эталонной жидкости (1 г/см3), - плотность исследуемой жидкости (1,5 г/см3).
- плотность исследуемой жидкости (1,5 г/см3).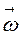 », т.к. все токи при таком вращении поворачиваются на один и тот же угол «j», движутся с одинаковой угловой скоростью «
», т.к. все токи при таком вращении поворачиваются на один и тот же угол «j», движутся с одинаковой угловой скоростью «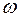 = dj/dt;
= dj/dt;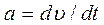 – угловое ускорение
– угловое ускорение 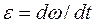 ;
;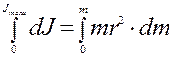 ;
;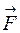 - момент силы
- момент силы 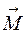 , характеризующий вращающее действие силы;
, характеризующий вращающее действие силы;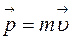 - момент импульса тела
- момент импульса тела 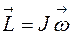 .
. (12)
(12) (13)
(13) (15)
(15)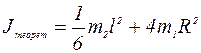 в работе проверяется справедливость основного уравнения динамики вращательного движения e = M/J.
в работе проверяется справедливость основного уравнения динамики вращательного движения e = M/J.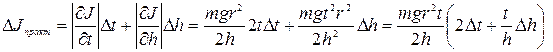 , (16)
, (16) .
. (17)
(17)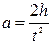 м/с2
м/с2
 a/r
1/с2
a/r
1/с2
 кг.м2
кг.м2
 кг.м2
кг.м2

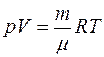 ,
,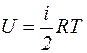 , (1)
, (1)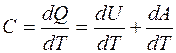
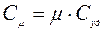
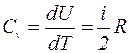 . (2)
. (2)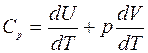 . (3)
. (3)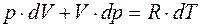 . (4)
. (4)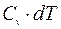 , получим окончательно:
, получим окончательно: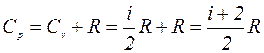 . (5)
. (5)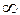 .
.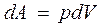
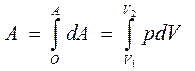
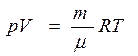
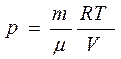
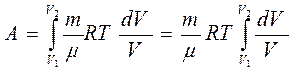
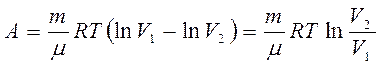
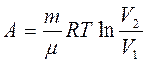
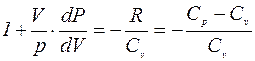 или
или 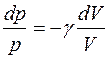 , (7)
, (7)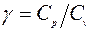 - отношение теплоемкостей, называемое показателем адиабаты.
- отношение теплоемкостей, называемое показателем адиабаты.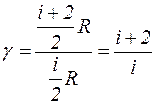 . (8)
. (8)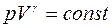 . (9)
. (9)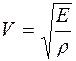 , (10)
, (10)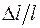 и приложенным к нему напряжением
и приложенным к нему напряжением 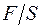 (т.е. растягивающей силе на единицу площади):
(т.е. растягивающей силе на единицу площади): , откуда
, откуда 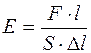 .
.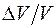 , а роль напряжения играет изменение давленая, Dр. Полагая изменения объёма и давления бесконечно малыми и принимая во внимание, что увеличение давления соответствует уменьшению объёма, для модуля упругости газа можно написать равенство:
, а роль напряжения играет изменение давленая, Dр. Полагая изменения объёма и давления бесконечно малыми и принимая во внимание, что увеличение давления соответствует уменьшению объёма, для модуля упругости газа можно написать равенство: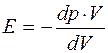 . (11)
. (11)


