
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метрология и технические измеренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЛЕКЦИЯ 1 МЕТРОЛОГИЯ И ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ
1.1.Понятие о метрологии и основные положения государственной системы измерений. В практической жизни человек часто имеет дело с измерениями, которые являются одним из важнейших путей познания природы. Отраслью науки изучающей измерения является метрология. Метрология в современном понимании наука об измерениях 6методах и средствах обеспечения их единства и способах достижения требуемой точности. Единством измерений называется состояние измерений, при которых результаты выражены в узаконенных единицах и погрешности известны с заданной вероятностью. ГСИ предусматривает комплекс взаимосвязанных правил и положений требований и норм, определяющих организацию и методику проведения работ по оценке и обеспечению точности измерений, результаты которых используются государственными органами предприятиями и учреждениями РФ. Основополагающими стандартами системы регламентируются: · единицы физических величин, допущенные к применению в РФ; · термины и определения из области метрологии; · нормируемые метрологические характеристики средств измерений; · организация и порядок проведения государственных испытаний средств измерений; · организация и порядок проведения поверки6 ревизии и экспертизы средств измерений; показатели точности измерений и формы представления результатов измерений; методика выполнения измерений. В большинстве стран мира мероприятия по обеспечению единства измерений установлены законодательно. Поэтому один из разделов метрологии называется законодательной метрологией и включает комплекс общих правил, требований и норм, направленный на обеспечение единства измерений. Для введения единообразия в единицах измерений в 1978 г был утвержден СТСЭ 1052-78 «Единицы физических величин» (СИ) который введен в РФ с 1 января 1979 г как обязательный во всех отраслях народного хозяйства, науки, техники и при преподавании. Система (СИ) исключает необходимость подробного изучения множества систем единиц. Система (СИ) содержит семь основных единиц, которые затрагивают измерения всевозможных параметров: механических, тепловых, электрических, магнитных, световых, акустических и ионизирующих излучений в области химии. Основными единицами установлены метр (М)- для измерения длины; килограмм (КГ)-для измерения массы; секунда (С)-для измерения времени; Кельвин (К)-для измерения температуры; ампер (А) - для измерения силы электрического тока; кандела (свеча) кД –для измерения силы света и моль –для измерения количества вещества.
1.2.Основы технических измерений ЛЕКЦИЯ 2 1.5.Методы измерений
Методы измерений – это совокупность приемов использования принципов и средств измерений. Все без исключения методы измерений являются разновидностями одного единственного метода – метода сравнения с мерой, при котором измеряемую величину сравнивают с величиной, воспроизводимой мерой (однозначной или многозначной). Различают следующие виды этого метода: метод непосредственной оценки, в котором значение измеряемой величины определяют непосредственно по отсчетному устройству многозначной меры, на которую непосредственно действует сигнал измерительной информации. При особо точных измерениях применяют метод сравнения с мерой, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой. Метод противопоставления – это метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами. Этот метод позволяет уменьшить воздействие на результаты измерения влияющих величин, так как они более или менее равномерно искажают сигналы измерительной информации как в цепи преобразования измеряемой величины так и в цепи преобразования величины, воспроизводимой мерой. Дифференциальный метод – это метод, в котором на прибор сравнения воздействует разность измеряемой величины и величины, воспроизводимой мерой. Нулевой метод – метод, в котором результирующий эффект воздействия величин на прибор сравнения равен нулю. Метод замещения – метод, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой. Метод совпадений – метод, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение меток шкал или периодических сигналов.
Единство измерения – это состояние измерений, при котором их результаты выражены в узаконенных единицах и погрешности измерений известны с заданной вероятностью. Единство измерений достигается путем точного воспроизведения и хранения установленных единиц физических величин и передачи их размеров применяемым средствам измерений. Воспроизведение, хранение и передачу размеров единиц осуществляют с помощью эталонов и образцовых средств измерений. Следовательно, высшим звеном в метрологической цепи передачи размеров единиц измерений являются эталоны. Эталоны – это средство измерений (или комплекс средств измерений), обеспечивающее воспроизведение и хранение единиц с целью Схема классификации эталонов Государственный эталон
Эталон копияЭталон сравненияРабочий эталон передачи ее размера нижестоящим по поверочной схеме средствам измерений, выполненное по особой спецификации и официально утвержденное в установленном порядке. Если прямая передача размера единицы от первичного эталона либо технически неосуществима, либо приводит к большой погрешности, целесообразно создавать специальный эталон, передача от которого не сопряжена с переходом от одних условий к другим, резко отличным от первых. Первичный или специальный эталон, официально утвержденный Госстандартом в качестве исходного для страны, называется государственным. Хранение единиц в состоянии, обеспечивающем неизменность ее размера во времени, и передачу размеров единиц всем применяемым в стране средствам измерения осуществляют с помощью вторичных эталонов и образцовых измерений. Вторичные эталоны создают и утверждают в случаях необходимости организации поверочных и предохранения государственного эталона от излишнего износа. Действительное значение величины, воспроизводимой вторичным эталоном (действительное значение эталона), устанавливается по результатам его сличений с соответствующим государственным эталоном. По метрологическому назначению вторичные эталоны делятся на эталоны – копии, эталоны сравнения и рабочие. Эталон – копию применяют вместо государственного эталона для хранения единицы и передачи ее размера рабочим эталонам. Он не всегда является физической копией государственного эталона, а применяется в качестве копии только по метрологическому назначению. Эталон сравнения применяют для сличения эталонов, которые по тем или иным причинам не могут быть непосредственно сличаемы друг с другом (находятся в различных органах метрологической службы и их нельзя транспортировать). Рабочий эталон применяют для хранения единицы и передачи ее размера образцовым средствам измерения высшего разряда и при необходимости наиболее точным рабочим мерам и измерительным приборам. Допускается применение государственного эталона в качестве рабочего, если это предусмотрено правилами хранения и применения эталона. Одиночный эталон состоит из одной меры, одного измерительного прибора или оной измерительной установки, обеспечивающих воспроизведение или хранение единицы самостоятельно, без других средств измерений того же типа. Групповой эталон состоит из совокупности однотипных мер, измерительных приборов или других средств измерений, применяемых как одно целое для повышения надежности хранения единицы. Размер единицы, хранимой групповым эталоном, определяется как среднее арифметическое из значений, найденных с помощью отдельных мер или измерительных приборов, входящих в групповой эталон.
Эталонный набор представляет собой набор мер или набор измерительных приборов, позволяющих хранить единицу или измерить величину в определенном диапазоне в котором отдельные меры или измерительные приборы набора имеют различные номинальные значения или поддиапазоны значений величины. Аналогично групповым эталонам различают эталонные наборы постоянного или переменного состава. 1.6. Погрешности измерений, критерий качества измерений
Качество измерений характеризуется точностью, достоверностью, правильностью, сходимостью и воспроизводимостью измерений, а также размером допустимых погрешностей. Точность – это качество измерений, отражающее близость их результатов к истинному значению измеряемой величины. Высокая точность измерений соответствует малым погрешностям как систематическим, так и случайным. Точность количественно оценивают обратной величиной модуля относительной погрешности. Достоверность измерений характеризует степень доверия к результатам измерений. Достоверность оценки погрешностей определяют на основе законов теории вероятностей и математической статистики. Это дает возможность для каждого конкретного случая выбирать средства и методы измерений, обеспечивающие получение результата, погрешности которого не превышают заданных границ с необходимой достоверностью. Под правильностью измерений понимают качество измерений, отражающее близость к нулю систематических погрешностей в результатах измерений. Сходимость – это качество измерений, отражающее близость друг к другу результатов измерений, выполненных в одинаковых условиях. Сходимость измерений отражает влияние случайных погрешностей. Воспроизводимость – это такое качество измерений, которое отражает близость друг к другу результатов измерений, выполненных в различных условиях (в различное время, в разных местах, разными методами и средствами). Погрешность измерения – это отклонение результата измерения от истинного (действительного) значения измеряемой величины. Погрешность измерений представляет собой сумму целого ряда составляющих, каждая из которых имеет свою причину. Можно выделить следующие группы причин возникновения погрешностей, связанных:
· с операцией настройки средств измерений или со смещением уровня настройки средства измерений во время эксплуатации; · с установкой объекта измерения на измерительную позицию; · с процессом получения, преобразования и выдачи информации в измерительной цепи средства измерения или обусловленных: · внешними воздействиями на средство и объект измерений (изменением температуры и давления, влиянием электрического и магнитного полей, вибрацией и т.п.); · свойствами измеряемого объекта; · квалификацией и состоянием оператора и т.л. Анализируя причины возникновения погрешностей, необходимо в первую очередь выявить те из них, которые оказывают существенное влияние на результат измерения. Анализ должен проводиться в определенной последовательности.
1.7.Абсолютная и относительная погрешности измерения
. В зависимости от формы выражения различают абсолютную и относительную погрешности измерений. Абсолютной называют погрешности измерений (D), выраженную в тех же единицах, что и измеряемая величина и определяют по формулам D=A-Cист; D=A-Cист@A-Cд где А – результат измерений, Хист—истинное значение измеряемой величины; Хд –действительное значение измеряемой величины. Относительная погрешность измерения (d) представляет собой отношение абсолютной погрешности измерения к истинному (действительному) значению измеряемой величины и выражается в процентах или долях измеряемой величины. Относительную погрешность в (%) определяют по формулам
d= (А – Хист)/Cист = D/Cист d=(A-Cд)/Cд *100
1.8.Статическая и динамическая погрешности
В зависимости от условий и режимов измерения различают статическую и динамическую погрешности. Статической называют погрешность, не зависящую от скорости изменения измеряемой величины во времени. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Динамической называют погрешность, зависящую от скорости изменения измеряемой величины во времени. Возникновение динамической погрешности обусловлено инерционностью элементов измерительной цепи средства измерения, т.е. тем, что преобразования в измерительной цепи не происходит мгновенно, а требует некоторого времени. Динамической погрешностью средства измерений является разность между погрешностью средства измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. 1.9.Систематическая и случайная погрешности измерений, грубые погрешности и промахи
В зависимости от характера проявления, возможностей устранения и причин возникновения различают систематическую и случайную погрешности. Систематической Dс называют составляющую погрешности измерений, остающуюся постоянной или закономерно изменяющуюся при повторных измерениях одной и той же величины. Причинами возникновения систематических составляющих погрешности измерения (систематических погрешностей) являются: · отклонения параметров реального средства измерений от расчетных значений, предусмотренных схемой;
· неуравновешенность некоторых деталей средства измерений относительно их оси вращения, приводящая к дополнительному повороту за счет зазоров, имеющихся в механизме; · упругая деформация деталей средства измерений, имеющих малую жесткость и приводящая к дополнительным перемещениям; · погрешность градуировки или небольшой сдвиг шкалы; · неравномерный износ направляющих устройств для базирования измеряемых деталей; · износ рабочих поверхностей деталей средства измерений, с помощью которых осуществляется контакт звеньев механизма; · усталостные изменения упругих свойств деталей, а также их естественное старение; · неисправности средства измерений. Ряд постоянных систематических погрешностей внешне себя не проявляют. Обнаружить их можно при поверке путем сравнения рабочих средств измерений с образцовым. Случайной D называют составляющую погрешности измерений, изменяющуюся случайным образом при повторных измерениях одной и той же величины. При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений одной и той же постоянной, неизменяющейся величины мы получаем результаты измерений – некоторые из них отличаются друг от друга, а некоторые совпадают. Такие расхождения в результатах измерений говорят о наличии в них случайных составляющих погрешности. Случайная погрешность возникает: при одновременном воздействии многих источников, каждый из которых сам по себе оказывает незаметное влияние на результат измерений, но суммарное воздействие всех источников может оказаться достаточно сильным. Грубые погрешности и промахи возникают: из-за ошибок или неправильных действий оператора (его психофизиологического состояния, неверного отсчета, ошибок в записях или вычислениях, неправильного включения приборов и т.п.); а так же при кратковременных резких изменениях условий проведения измерений (вибрации, поступлении холодного воздуха, толчки прибора оператором и т.п.). Если грубые погрешности и промахи обнаруживают в процессе измерений, то результаты, содержащие их отбрасывают. Однако чаще всего их выявляют только при окончательной обработке результатов измерений с помощью специальных критериев оценки грубых погрешностей. ЛЕКЦИЯ 3 1.10.Определение показателей точности прямых измерений с многократными независимыми наблюдениями
Порядок и методику выполнения прямых измерений с многократными независимыми наблюдениями, обработки результатов наблюдений и оценки их погрешностей регламентирует стандарт. При статистической обработке результатов наблюдений выполняют следующие операции: · исключение известных систематических погрешностей из результатов наблюдений; · вычисление: среднего арифметического исправленных результатов наблюдений, принимаемого за результат измерения; оценки среднего квадратического отклонения результата наблюдений; доверительных границ случайной составляющей погрешности результата измерения (при этом проверяют гипотезу о том, что результаты наблюдений принадлежат нормальному распределению); не исключенной систематической погрешности (не исключенных остатков систематической погрешности) результата измерения. 1.11. Исключение известных систематических погрешностей из результатов наблюдений
Систематические погрешности исключают путем: · ликвидации источников погрешностей до начала измерений; · исключения погрешностей в процессе измерения способами замещения, компенсации погрешности по знаку, противопоставления, систематических наблюдений; · внесения вычисленных поправок в результат измерения. -Примечание: 1) Поправкой называют значение величины, одноименной с измеряемой, которое прибавляют к полученному при измерении значению величины с целью исключения систематической погрешности. 2) Поправочный множитель – это число, на которое умножают результат измерения с целью исключения систематической погрешности. 3) Поправку, вводимую в показание измерительного прибора, называют поправкой к показаниям прибора.
1.12.Вычисление среднего арифметического исправленных результатов наблюдений
Вычисленные средние арифметические значения неисправленных результатов наблюдений и отклонений от них результатов наблюдений будут также неисправленными. Их определяют по формулам.
Сумму систематических погрешностей, входящих в неисправленные результаты наблюдений, для каждого i-го наблюдения обозначим
но В этом случае случайные отклонения результатов наблюдений от среднего арифметических значений отличаются от неисправленных отклонений:
Если систематические погрешности, т. е. Если необходимо предварительно исправить отдельные результаты наблюдений, то в них вводят поправки, равные систематическим погрешностям по числовому значению и обратные им по знаку. Таким образом, за результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения систематических погрешностей. Поправки определяют экспериментально при проверке средств измерений или по результатам специальных исследований. Для исправления результата наблюдения его складывают только со средним арифметическим значением поправки.
Где хi, x΄i – соответственно исправленный и неисправленный результаты наблюдений; p – среднее арифметическое значение поправки. Следует заметить, что введением поправки устраняют влияние только одной определенной систематической погрешности, а поэтому в результаты измерений приходится иногда вводить большое число поправок. Ограниченная точность определения поправок приводит к накоплению случайных погрешностей, в результате чего дисперсия результата измерения увеличивается. Поэтому экспериментатор должен определить оптимальную границу значений поправок, которые следует вводить в результаты наблюдений для получения более достоверных сведений об истинном значении измеряемой величины.
1.13.Оценка среднего квадратического отклонения результатов наблюдений
Несмещенной состоятельной, эффективной оценкой для генерального среднего ā нормального распределения является выборочное среднее х, определяемое по формуле:
Где х1; х2;…;хn – совокупность значений случайных величин х. Несмещенную оценку для среднего квадратического отклонения определяют по формуле:
где если a неизвестно, то по формуле (1):
если а известно, то по формуле (2):
Значение коэффициента Мк дается в таблице, где к = n-1, если а неизвестно, и к = n, если а известно. При значениях объема выборок n > 60 оценку для среднего квадратического отклонения σ находят по формуле (1), а если а неизвестно, или по формуле (2), если а известно. Несмещенными оценками для дисперсии σ2 нормального распределения являются выборочные характеристики: при неизвестном а
при известном а
1.14.Оценка среднего квадратического отклонения результата измерения
Среднее квадратическое отклонение результата измерения оценивают по формуле: где S(Ã) – оценка среднего квадратического отклонения результата измерения; Ã – результат измерения (ср. арифметическое исправленных результатов наблюдений); хi – i-й результат наблюдений.
1.15. Вычисление доверительных границ случайной погрешности результата измерения
Доверительные границы случайной погрешности результата измерения устанавливают для результатов наблюдений, принадлежащих нормальному распределению. Если это условие не выполняется, то методы вычисления доверительного интервала случайной погрешности должны быть указаны в методике выполнения конкретных измерений. Если заранее известно, что результаты наблюдений принадлежат нормальному распределению, доверительные границы Є (без учета знака) случайной погрешности результата измерения находят по формуле: Є=tsS( Где ts – коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа результатов наблюдений n находят по таблицам. При числе наблюдений n > 50 для проверки принадлежности их к нормальному распределению используют критерий х2 (Пирсона) или ω2 (Мизеса-Смирнова). Если 50 > n > 15, то используют составной критерий. 1.16. Вычисление доверительных границ погрешности результата измерения Если отношение неисключенных систематических погрешностей к среднему квадратическому отклонению результата измерения Q/S(Ã) < 0,8, то неисключенными систематическими погрешностями пренебрегают и принимают что граница погрешности результата ∆ = Є. Если Q/S(Ã) > 8, то пренебрегают случайной погрешностью и принимают, что граница погрешности результата Δ = Q. Однако, следует помнить, что погрешность, возникающая вследствие пренебрежения одной из составляющих погрешности результата измерений при выполнении указанных неравенств, не должна превышать 15 %. Если неравенства не выполняются, то границу погрешности результата измерения находят путем построения композиции распределений случайных и не исключенных систематических погрешностей, рассматриваемых как случайные величины. В результате определения доверительных границ случайных погрешностей, вычисляют границы погрешности результата измерения Δ без учета знака по формуле: Δ = К*SΣ Где К – коэффициент, зависящий от соотношения случайной и неслучайной систематической погрешностей; SΣ – оценка суммарного среднего квадратического отклонения результата измерения.
Суммарное среднее квадратического отклонение результата измерения оценивают по формуле: Є
1.17. Определение показателей точности прямых однократных измерений, оценивание погрешностей результатов измерений
Порядок и методика выполнения прямых однократных измерений при условии, что составляющие погрешности результата известны, случайные погрешности составляющих распределены нормально, а не исключенные систематические погрешности, представлены заданными границами ± Под границами не исключенной систематической погрешности измерений понимают границы интервала, найденные нестатистическими методами, внутри которого находится неисключенная систематическая погрешность измерения. Погрешность измерения задается границами в том случае, когда сведения о вероятности нахождения ее в этих границах отсутствуют. За результат однократного измерения Ã принимают значение величины, полученное при отдельном наблюдении. Составляющие погрешности результата измерений должны быть известны до проведения измерений, предполагая, что известные систематические погрешности исключены. Условия проведения однократных измерений заключается в следующем: производственная необходимость (разрушение образца, невозможность повторных измерений, экономическая целесообразность и т. д.); возможность пренебрежения случайными погрешностями. Следует отметить, что случайные погрешности считают пренебрежимо малыми по сравнению с не исключенными систематическими, если Где Случайные погрешности существенны, но доверительная граница погрешности результата измерения не превышает допускаемой погрешности измерений. До начала измерений проводят априорную оценку погрешности результата измерения, используя предварительные данные об измеряемой величине, условиях измерения и источниках погрешностей измерения (составляющих погрешности измерения). Если априорная оценка превышает допускаемую погрешность результата измерений, то выбирают более точное средство измерений или изменяют методику выполнения измерений. ЛЕКЦИЯ 4 Для определения доверительных границ погрешности результата измерения принимают вероятность, равную 0,95. В особых случаях, например, при измерениях, которые нельзя повторить, допускается указывать доверительные границы для более высоких вероятностей. Составляющими погрешности результата однократного измерения являются погрешности: средств измерений, метода, оператора. Погрешности средств измерений, метода и оператора могут состоять из не исключенных систематических и случайных погрешностей. Не исключенные систематические погрешности могут быть выражены одним из способов: границами ± доверительными границами ± Случайные погрешности могут быть выражены одним из способов: средним квадратическим отклонением S; доверительными границами ± Є (Р) Погрешности средств измерений определяют по метрологическим характеристикам, которые указаны в нормативно-технической документации и в соответствии с РД 50-453-84. Погрешности метода и оператора должны быть определены в НТД на конкретную МВИ (метод выполнения измерений). Если неисключенная систематическая погрешность имеет место только у одной из составляющих (погрешности средства измерений, или метода, или оператора), то не исключенную систематическую погрешность результата выражают границами этой погрешности. Доверительные границы не исключенной систематической погрешности результата измерения вычисляют следующим образом. При наличии нескольких не исключенных систематических погрешностей, заданных своими границами Qj, доверительную границу не исключенной систематической погрешности результата измерения Q (P) (без учета знака) вычисляют по формуле:
Где к – поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих При доверительной вероятности Р = 0,90 поправочный коэффициент к принимают 0,95; при Р = 0,95 – к = 1,1. При доверительной вероятности Р = 0,99 – к = 1, 45, при m > 4; ~ 1,4 при m = 4; ~ 1,3 при m = 3; ~ 1,2 при m = 2. Более точное значение к для Р = 0,99 при числе соответствующих m ≤ 4 в зависимости от соотношения составляющих l определяют по графику в соответствии с требованиями ГОСТ 8.207-76.
Погрешность возникающая при использовании формулы для суммирования не исключенных систематических погрешностей и при нахождении поправочного коэффициента к для доверительной вероятности Р = 0,99 по графику k = f (m,l) не превышает 5 %. При наличии нескольких неисключительных систематических погрешностей, заданных доверительными границами Qj (Pj) рассчитанными по формуле, доверительную границу неисключенной систематической погрешности результата однократного измерения вычисляют по формуле
Где Доверительные границы случайной погрешности результата измерения вычисляют следующим образом. Если случайные погрешности средств измерений (метода, оператора) представлены средними квадратическими отклонениями Si, приведенными в технической документации, то среднее квадратическое отклонение результата однократного измерен ия S (Ã) вычисляют по формуле: Где m – число составляющих. Доверительную границу случайной погрешности результата измерения Є (Р) вычисляют по формуле: Є(Р) Где Zp/2 – P/2 – точка нормированной функции Лапласа, отвечающая вероятности Р. если доверительная вероятность Р = 0,95, то Z0,95/2 = 2, если Р = 0,99, то Z0,99/2 = 2,6. Если случайные погрешности средств измерений (метода, оператора) представлены доверительными границами Є(Р), соответствующими одной и той же вероятности, то доверительные границы случайной погрешности результата однократного измерения вычисляют по формуле:
Если случайные погрешности средств измерений (метода, оператора) определяют предварительно экспериментально при ограниченном числе измерений (n < 30), то доверительную границу этой случайной составляющей вычисляют по формуле:
Где t – коэффициент, зависящий от доверительной вероятности и числа измерений. В качестве коэффициента t можно использовать коэффициент Стьюдента, соответствующий числу степеней свободы той составляющей, оценка которой произведена при наименьшем числе измерений; Si – оценка среднего квадратического отклонения i-й составляющей (погрешности средств измерений, метода, оператора). Если случайные погрешности средств измерений (метода,оператора) представлены доверительных границами, соответствующими разным вероятностям, то сначала определяют среднее квадратическое отклонение результата измерения по формуле:
а потом вычисляют доверительные границы случайной погрешности результата измерений по формуле:
если доверительные границы случайных погрешностей для некоторых составляющих определены экспериментально, то рассчитанные доверительные границы результата измерений будут несколько завышены. Если погрешности метода и оператора пренебрежимо малы по сравнению с погрешностью используемых средств измерений (не превышают 15 % от погрешности средств измерений), Если Если Если то доверительную границу погрешности результата измерений вычисляют по формуле:
где значение k для доверительной вероятности 0,95 и 0,99 в зависимости
. 1.18. Определение результатов косвенных измерений и оценивание их погрешностей
Основные положения определения результатов измерений и оценивание их
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.36.252 (0.014 с.) |



 Первичный эталонСпециальный эталон
Первичный эталонСпециальный эталон
 Вторичные эталоны
Вторичные эталоны


 ;
; 
 i. Их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на какую-то величину
i. Их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на какую-то величину  , которая является систематической погрешностью неисправленного среднего арифметического
, которая является систематической погрешностью неисправленного среднего арифметического Тогда
Тогда


 i = 1, 2,…,n то qi=q´i, и неисправленные отклонения могут быть использованы для оценки рассеивания ряда наблюдений.
i = 1, 2,…,n то qi=q´i, и неисправленные отклонения могут быть использованы для оценки рассеивания ряда наблюдений. i = -
i = -  i
i


 (1)
(1) (2)
(2)


 )
)
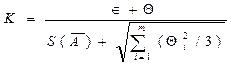

 .
. .
.
 .
.





 то за погрешность результата измерений принимают погрешность используемых средств измерений.
то за погрешность результата измерений принимают погрешность используемых средств измерений. то не исключенными систематическими погрешностями пренебрегают и принимают в качестве погрешности результата измерения доверительные границы случайных погрешностей, как указано выше.
то не исключенными систематическими погрешностями пренебрегают и принимают в качестве погрешности результата измерения доверительные границы случайных погрешностей, как указано выше. то случайными погрешностями пренебрегают и принимают в качестве погрешности результата измерения границы не исключенных систематических погрешностей.
то случайными погрешностями пренебрегают и принимают в качестве погрешности результата измерения границы не исключенных систематических погрешностей.






